Сборник задач по курсу «Теория вероятностей и математическая статистика»

1. Пусть имеются 5 пронумерованных карточек с буквами: П ₁ У ₂ Р ₃ Г ₄ А ₅ (в нижнем углу стоят номера карточек). Карточки перемешиваются, а затем снова выкладываются наугад (т. е. в случайном порядке). Какова вероятность, что получится слово ПУРГА?

2. Имеется 6 карточек с буквами К ₁ Н ₂ И ₃ Г ₄ А ₅ А ₆ . Карточки перемешиваются и взятые наудачу 5 из них снова выкладываются в случайном порядке. Какова вероятность, что получится слово КНИГА?

3. Бросаются две правильных игральных кости. Какова вероятность, что сумма выпавших очков окажется больше их произведения?

4. Четырёхтомное сочинение расположено на полке в произвольном порядке. Какова вероятность, что номера томов идут подряд?

5. В корзине находится 10 шаров, из которых 7 белых и 3 черных. Шары перемешивают и наугад вынимают 6 шаров. Какова вероятность событий: А – все шары белые, В – белых ровно 4.

6. Бросается кубик. Какова вероятность, что выпало либо четное число очков, либо 3?

7. в классе из 27 учеников был произведен опрос. На вопрос о том, кто хорошо знает алгебру, подняли руки 17 человек. На вопрос о том, кто хорошо знает геометрию, подняли руки 6 человек. На вопрос о том, кто хорошо знает оба предмета, подняли руки 2 человека. Какова вероятность того, что случайно выбранный турист из группы хорошо знает алгебру или геометрию?

8. На пустую шахматную доску случайным образом ставятся 3 фигуры. Найти вероятность того, что хотя бы на одно угловое поле будет поставлена фигура.

9. Вероятность того, что рабочий перевыполнит план, равна 0,8, а вероятность того, что в случае перевыполнения плана он не получит премию, равна 0,1. Какова вероятность того, что рабочий получит премию?

10. Определить вероятность того, что партия из 100 изделий, среди которых 7 бракованных, будет принята при испытании наудачу выбранной половины всей партии, если условиями приема допускается не более одной бракованной из 50?

11. Из колоды наугад вынимается карта. Событие А – вынут туз, событие В – вынута карта черной масти. Зависимы ли эти события?

12. На машину поставлено 3 противоугонных устройства, работающие независимо друг от друга. Вероятность того, что при попытке угона срабатывает первое равно 0,7 , второе срабатывает с вероятностью 0,9 , третье 0,1 . Каковы вероятности следующих событий: А – при попытке угона сработали все устройства, В – сработало хотя бы одно (т.е. попытка угона не удалась).

13. Бросается 2 кубика. Какова вероятность, что на них выпадут различные числа?

14. Вероятность попадания стрелком в десятку равна 0.7, а в девятку – 0.2. Какова вероятность, что за 3 выстрела стрелок наберёт как минимум 29 очков?

15. В барабане револьвера 7 гнёзд и вставлено 5 патронов. Дважды барабан наугад прокручивается, и каждый раз нажимается курок. Какова вероятность, что выстрела не будет?

16. Прибор состоит из двух дублирующих блоков и остаётся работоспособным, если исправен хотя бы один из них. Случайным образом прибор может находиться в одном из двух режимов: благоприятном – с вероятностью 0.9 и неблагоприятном – с вероятностью 0.1. В благоприятном режиме надёжность (т.е. вероятность безотказной работы) каждого из блоков есть 0.95, а в неблагоприятном – 0.80. Учитывая всё это найти безусловную (полную) надёжность прибора.

17. В корзине имеется 4 белых и 2 черных шара (т. е. всего 6 шаров). Из нее наугад вынимают один шар. Если он черный, то его кладут обратно, шары перемешивают и снова наугад достают шар. Это повторяется до тех пор, пока не будет вынут белый шар. Какова вероятность, что понадобится: а) ровно 4 вынимания, б) не более трех выниманий?

18. Кубик подбрасывается до тех пор, пока не выпадет 6. Найти вероятность того, что понадобится: а) ровно 3 подбрасывания, б) не более трех подбрасываний.

19. Некто предлагает пари на то, что за 25 попыток, в каждой из которых одновременно бросаются две игральные кости, он обязательно выбросит хотя бы один раз две пятерки. Какова вероятность, что предложивший человек выиграет это пари?

20. Есть три стрелка, которые попадают в мишень с вероятностями р₁ = 0,7, р₂ = 0,8 и р₃ = 0,9 соответственно. Какова вероятность поражения мишени при выстреле по ней всех стрелков залпом?

21. Вероятность попадания стрелка в мишень в каждом выстреле р = 0,8. Какова вероятность поражения мишени при четырех выстрелах?

22. Один самолет после бомбометания поражает некую цель с вероятностью р = 0,3. Сколько самолетов необходимо послать на задание, чтобы цель была уничтожена с вероятностью большей, чем 0,8?

23. Пусть вероятность поражения цели при бомбометании с самолёта есть 0.35. И пусть независимо бросаются 10 бомб. Какова вероятность, что цель поразят ровно 3 (наивероятное число) бомбы?

24. Вероятность выигрыша по лотерейному билету равна 0,2 (т. е. выигрывает в среднем 2 билета из 10). Сколько нужно купить билетов, чтобы выиграть хотя бы по одному из них с вероятностью большей, чем 0,95 (т. е. почти наверняка)?

25. Предприятие изготавливает 95 % стандартных деталей, из которых 86 % первого сорта (остальные, по-видимому, второго и третьего). Найти вероятность, что взятое наудачу изделие – 1 сорта .

26. Имеются 2 коробки с номерами 1 и 2, в каждой из которых по 12 шаров. В 1 коробке 3 белых шара и 9 черных, во второй 4 белых и 8 черных . Кроме коробок имеется корзина с 4 шарами, на трех из которых нарисована цифра 1, а на одном цифра 2. Сначала из корзины случайно выбирается один шар, а затем из коробки с номером вытащенного шара снова наугад вынимается шар. Какова вероятность, что он белый?

27. Электрическая цепь состоит из трех последовательно включенных и независимо работающих приборов. Вероятности выхода из строя первого, второго и третьего прибора соответственно равны 0,25, 0,05 и 0,1. Вычислить вероятность того, что в цепи не будет тока.

28. Известно, что тяжелоатлет в среднем перед одним из 10 соревнований принимает допинг. Анализ его результатов показывает, что без допинга он поднимает рекордный вес в 6 попытках из 9 (в среднем), а с допингом – в 8 попытках из 10 (в том же). Какова вероятность, что в данном соревновании он поднимет рекордный вес?

29. Солдат получает зачёт по стрельбе при условии, что в течение отведённого времени он поразит не менее трёх мишеней из пяти. Каждую мишень не зависимо от других солдат может поразить с вероятностью 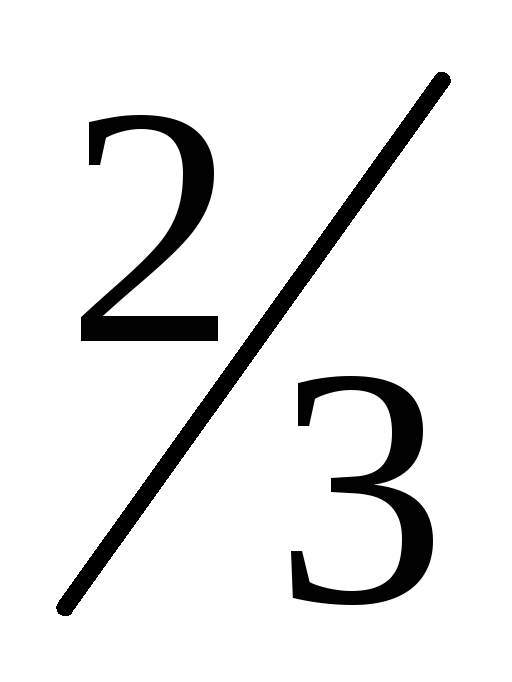. Какова вероятность, что он сдаст зачёт?

30. Четыре охотника пошли на охоту. Первый из них при выстреле попадает в цель с вероятностью 0,4, второй – 0,5, третий – 0,7, четвертый – 0,2. Увидев кабана, охотники сделали залп (т. е. одновременно выстрелили). Одним попаданием кабана можно убить с вероятностью 0,2, двумя – 0,6, а тремя – наверняка. Найти вероятность того, что кабан убит.

31. Группа в 30 студентов поровну состоит из отличников, хорошистов и троечников. Отличник на экзамене обязательно получит 5; хорошист – равновозможно 5 или 4; а троечник – равновозможно 4, 3 или 2. Новый преподаватель наугад вызывает незнакомого студента. Какова вероятность, что студент получит 4

32. Имеются 2 коробки с номерами 1 и 2, в каждой из которых по 12 шаров. В 1 коробке 3 белых шара и 9 черных, во второй 4 белых и 8 черных. Кроме коробок имеется корзина с тремя шарами, на двух из которых нарисована цифра 1, а на одном цифра 2. Сначала из корзины наугад выбрали один шар, а затем из коробки с номером вытащенного шара снова наугад вынули шар. Он оказался белым. Какова вероятность, что из корзины был вынут шар с номером 1?

33. 10 студентов пришли сдавать экзамен, включающий 20 вопросов. По качеству подготовки студентов можно разделить на 4 группы: 1) 2 человека подготовились отлично (знают ответы на все вопросы), 2) 5 человека подготовились хорошо (знают 16 из 20), 3) 2 человека подготовились удовлетворительно (знают 10 из 20), 4) один человек плохо подготовился (знает 5 из 20). Вызванный наугад студент ответил на 4 предложенных вопроса и получил отличную оценку. Можно ли быть уверенным, что оценка поставлена заслуженно?

34. Известно, что в среднем 1 из 700 мальчиков рождается с лишней Y-хромосомой. Среди таких детей агрессивное поведение встречается в среднем у 20 мальчиков из 21. У обычных детей такое поведение встречается намного реже – в одном случае из 21. У данного мальчика наблюдается агрессивное поведение. Велика ли вероятность, что у него лишняя Y-хромосома?

35. Какова вероятность, что при 12 подбросах кубика ровно 3 раза выпадет четное число очков?

36. Какова вероятность, что при 5 подбросах кубика не менее трех раз выпадет 6 очков?

37. В одном вузе вступительный тест по математике на заочное отделение состоял из 12 вопросов, к каждому из которых предлагалось 4 варианта ответов, среди которых только один правильный. Для успешного прохождения теста достаточно было правильно ответить не менее, чем на 4 вопроса. Найти вероятность прохождения теста для полностью неподготовленного абитуриента, который отмечает ответы наугад.

38. Вероятность выигрыша по лотерейному билету 0,05 (т. е. в среднем из 100 билетов 5 выигрышных). Какова вероятность выиграть хотя бы пару раз, купив 16 билетов?

39. Вероятность того, что в течение дня от клиента поступит заявка, для каждого клиента одинакова и равна 0,1. Определить, в каких границах находится число клиентов, если наивероятнейшее число заявок за день равно 3.

40. Вероятность успешного проведения испытания равна 0,8. Сколько надо провести испытаний, чтобы наивероятнейшее число успешных среди них было не менее пяти?

41. Применяемый метод лечения приводит к выздоровлению в 80 % случаев. Какова вероятность того, что из выбранных 10 больных при применении этого метода выздоровеет ровно 9?

42. Всхожесть семян данного растения равна 80 %. Найти вероятность того, что из шести посаженных семян взойдут не менее половины.

43. Некий игрок в настольный теннис играет в 3 раза хуже своего соперника. С какой вероятностью он выиграет матч из пяти партий?

44. В корзине 3 белых, 2 зеленых и 2 черных шара . Наугад вынимается 2 шара. Найти закон распределения с.в. Х – числа белых шаров среди вынутых.

45. Игральный кубик подбрасывается 3 раза. Найти выражение для функции распределения с.в. Х – числа выпавших двоек. Построить ее график.

46. Первый стрелок попадает в мишень с вероятностью 0.6, а второй 0.8 . Оба сделали по выстрелу. Найти функцию распределения с.в. Х – числа промахов по мишени.

47. Дана функция распределения с.в. Х: 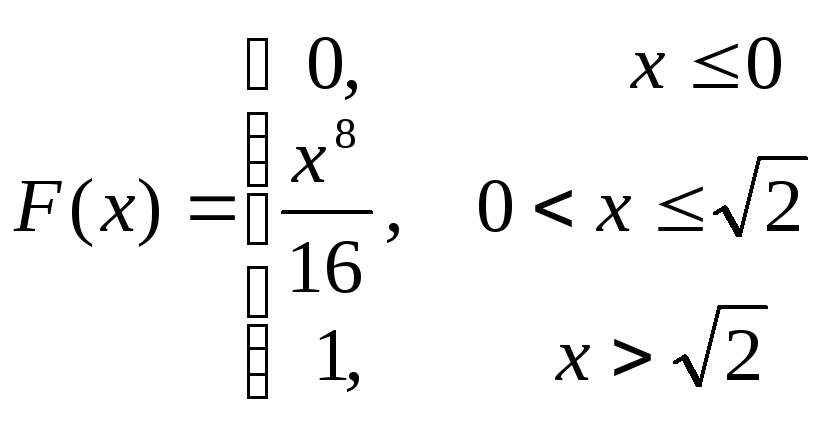. Найти вероятность того, что при испытании случайная величина примет значение из интервала (0,1). Найти вероятность, что при двух испытаниях этой с.в. она оба раза примет значение из интервала (0,1).

48. Дана функция распределения с.в. Х: 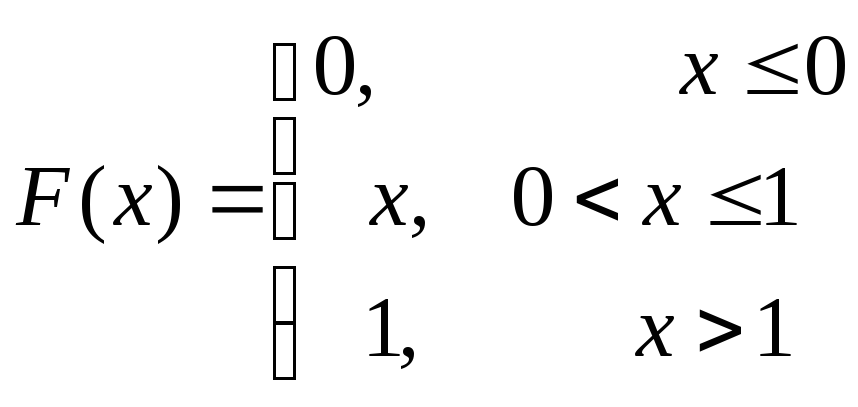. Найти плотность вероятностиf(x).

49. Дана плотность вероятности с.в. Х: 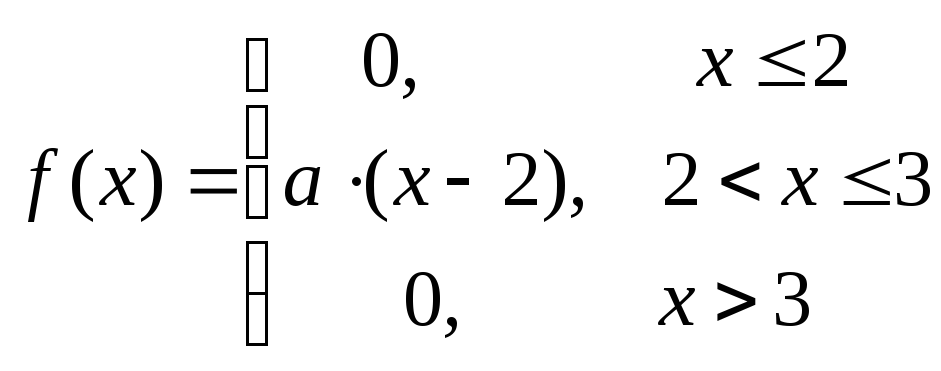. Найти а) значение параметраа; б) ; в) функцию распределенияF(x).

50. Случайная величина Х задана законом распределения

Х	−2	0	2
Р	0.3	0.6	0.1

Найти закон распределения с.в. Y =|Х| .

51. Подбрасываются 3 монеты (например, копейка, полтинник и рубль). Составить закон распределения с.в. Z – общего числа орлов на монетах.

52. Найти среднее число суммы очков , выпадающих на трех подброшенных кубиках .

53. Стрелок стреляет в первую мишень и попадает с вероятностью 0,8, а затем — во вторую и попадает с вероятностью 0,9. Построить график функции распределения числа попаданий в мишени.

54. В связке имеются 4 ключа, из которых только одним можно открыть дверь. Ключи пробуются один за другим в случайном порядке, причем ключ, оказавшийся неподходящим, больше не используется. Составить закон распределения и изобразить функцию распределения числа ключей, которые будут испробованы для открытия двери.

55. Кубик подбрасывают до первого выпадения шестерки, но не более 5 раз. Найти среднее число подбрасываний.

56. Найти математическое ожидание и медиану непрерывной с.в. Х, если плотность ее вероятности

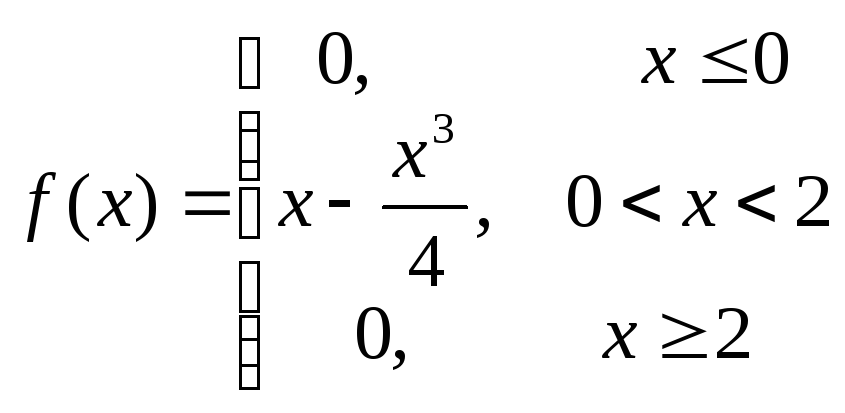
57. Пусть Х и Y – независимые с.в. . Найти математическое ожидание с.в. Z=2X–5Y+4X∙Y+3, если М(Х)=1, M(2Y+Х)=3.

58. Первый стрелок попадает в мишень с вероятностью р₁=0.5, второй с вероятностью р₂=0.6, а третий с вероятностью р₃=0.7 . Найти среднее число промахов по мишени при одном залпе этих стрелков по мишени.

59. Играющий платит некоторую сумму (начальная ставка) за проведение игры ее устроителю. Четыре раза бросается монета кубик. Если выпадает 4 шестерки, то играющий получает 100 рублей, если 3, то 10 рублей. В остальных случаях − ничего. Какова должна быть начальная ставка в игре, чтобы игра была «безобидной» (т.е. средний общий выигрыш с учетом начальной ставки равен 0).

60. Даны законы распределения независимых случайных величин Х и Y:

Х	1	2
Р	1/2	1/2

Y	0	1	3
Р	1/2	1/4	1/4

0000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000

Найти дисперсию случайной величины 2|Х|−Y²+5.

61. В ящике 5 белых шаров и 7 черных. Наугад вынимаю 2 шара. Найти дисперсию, среднее квадратическое отклонение и моду с.в. Х – числа белых шаров среди вынутых.

62. Первый стрелок попадает в мишень с вероятностью р₁=0.5, второй с вероятностью р₂=0.6, третий с вероятностью р₃=0.7, а четвертый с вероятностью р₃=0.8 . Найти моду, дисперсию и среднее квадратическое отклонение числа промахов по мишени при одном залпе этих стрелков по мишени.

63. Найти дисперсию с.в. Х – числа появлений события А в трех независимых испытаниях, если вероятности появления этого события одинаковы в каждом испытании, а среднее число появлений события в этих испытаниях равно 1.5 .

64. Д.с.в. Х принимает значения {–1, 0, 1} . Найти закон распределения этой с.в., если М(Х)=0.5, D(X)=2/3 .

65. Плотность вероятности н.с.в. Х задана формулой:

.

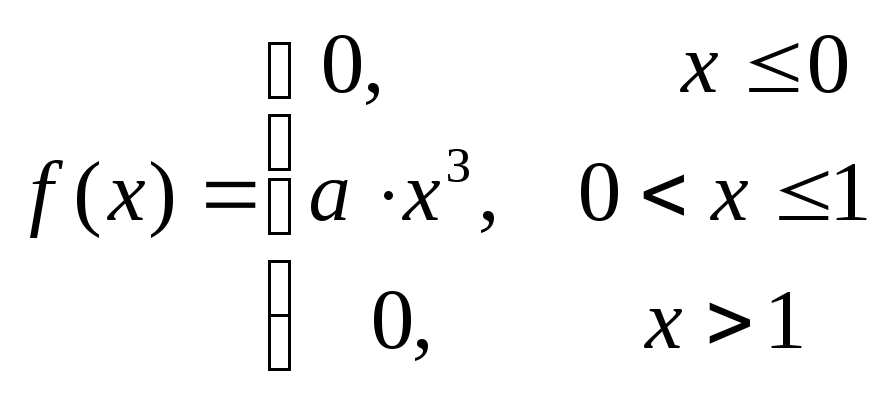Найти значение параметра а, математическое ожидание, медиану, дисперсию и среднее квадратическое отклонение этой случайной величины.

66. Дана плотность вероятности н.с.в. :

.

Найти значение параметра а, медиану и моду этой случайной величины.

67. Пара кубиков подбрасывается 100 раз. Каково наивероятнейшее число выпадений одинакового числа очков?

68. Два стрелка попадают в мишень с вероятностями 0.5 и 0.6 соответственно. Стрелки стреляют залпами по 50 мишеням по очереди. Найти среднее число пораженных мишеней.

69. Рабочий изготовил за месяц 5000 изделий. Вероятность выпуска бракованного изделия равна 0.0002 . Какова вероятность, что браковано 18 изделий? Каково среднее значение бракованных изделий? Каково наивероятнейшее число бракованных изделий и какова его вероятность?

70. Какова вероятность, что при 10 испытаниях нормально распределенной случайной величины Х хотя бы одно ее значение отклонится от среднего более, чем на удвоенное среднее квадратическое отклонение?

71. В связке имеются 4 ключа, из которых только одним можно открыть дверь. Ключи пробуются один за другим в случайном порядке, причем ключ, оказавшийся неподходящим, больше не используется. Составить закон распределения и изобразить функцию распределения числа ключей, которые будут испробованы для открытия двери.

72. Случайная величина Х принимает только 2 возможных значения, одно из этих значений равно – 4. Определить закон распределения X, если M(X) = 5, б(X) = 3.

73. Математическое ожидание нормально распределенной случайной величины равно 10, а среднее квадратическое отклонение равно 2,5. Выписать плотность вероятности и изобразить кривую распределения этой случайной величины.

74. Случайная величина Х имеет нормальное распределение, M(X) = 20. Вероятность того, что X примет значение, заключенное в интервале (15; 20) равна вероятности того, что значение X будет менее 15. Определить вероятность того, что X примет значение, большее 25.

75. Считая рост студента случайной величиной, распределенной по нормальному закону с параметрами a = 170 см и б = 25 см, найти:

а) вероятность того, что рост студента будет более 190 см;

б) интервал, в котором с вероятностью 0,95 будет заключен рост студента

в) вероятность того, что рост студента отклонится от математического ожидания менее чем на 10 см.

76. Случайные ошибки измерения подчиняются нормальному закону с математическим ожиданием, равным 0. Вероятность того, что ошибка не превзойдет по модулю 3 мм, равна 0,97. Найти дисперсию.

77. Производятся три взвешивания, при каждом из которых наблюдаются случайные ошибки, подчиненные нормальному закону с параметрами a = 0 г, б = 10 г. Вычислить вероятность того, что ошибка при каждом взвешивании будет не менее 5 г.

78. При тестировании группа студентов получила следующие оценки: 2, 5, 3, 2, 4, 2, 5, 2, 3, 2. Найти статистическое распределение выборки.

79. Построить полигон и гистограмму относительных частот по статистическому распределению выборки :

xi	1	2	3	4	5
ni	13	14	24	16	3

80. Пользуясь статистическим рядом относительных частот для выборки объема n=10 :

xi	0	1	2	3
wi	0.1	0.2	0.1	0.6

найти эмпирическую функцию распределения и построить ее график.

81. Дано статистическое распределение выборки объема n=30 :

xi	2	4	6
ni	3	10	17

Найти все числовые характеристики этого распределения.

82. Из 1500 деталей отобрали 250 . Дан интервальный ряд весов отобранных деталей:

размер	7.8 − 8.0	8.0 − 8.2	8.2 − 8.4	8.4 − 8.6	8.6 − 8.8	8.8 − 9.0
количество	5	20	80	95	40	10

Оценить средний вес детали и соответствующую дисперсию, найти моду.

83. Генеральная совокупность некоторого признака Х распределена нормально с известным средним квадратическим отклонением σ=2 . Для определения среднего значения признака Х была сделана выборка объема n=10, по которой вычислено выборочное среднее 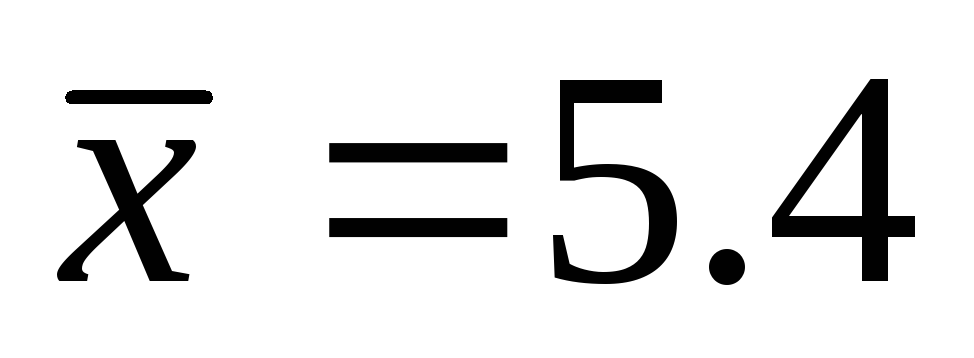. Найти доверительный интервал для математического ожиданияа признака Х с надежностью γ=0.95 .

84. Некоторый признак Х генеральной совокупности распределен нормально. Для определения среднего значения признака Х была сделана выборка объема n=12, по которой вычислено выборочное среднее 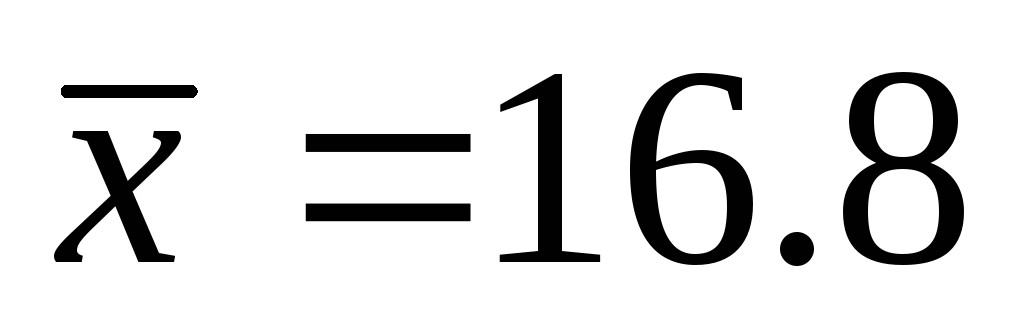и выборочное исправленное среднее квадратическое отклонениеs = 1.5 . Найти доверительный интервал для математического ожидания а признака Х с надежностью γ=0.95 .

85. Даны результаты выборочного обследования 100 заводов по производству инструментов по проценту выполнения плана

    Процент выпол- нения плана	0−20	20−40	40−60	60−80	80−100	100−120	120−140
    число заводов	2	7	16	18	23	20	8

• Построить гистограмму частот

• Найти несмещенные оценки генеральной средней и дисперсии

• В предположении, что генеральная совокупность распределена нормально, найти границы, в которых с доверительной вероятностью 0.9545 заключен средний процент выполнения плана.

Получены следующие выборочные данные о распределении доли лиц, не совершивших нового преступления после отбытого наказания (Y), в зависимости от срока отбытого наказания (X).

Хi, лет	1	2	3	4	5	6	7	8	9
Yi, %	61,8	56,1	50,8	47,6	42,3	39,5	35,7	29,4	25,1

Предполагая, что X и Y связаны линейной зависимостью, найти выборочное уравнение линейной регрессии Y на X, изобразить его графически.

87. С целью анализа взаимного влияния заработной платы и текучести рабочей силы на пяти однотипных фирмах с одинаковым числом работников произведены измерения уровня месячной зарплаты Х и числа уволившихся за год работников Y. Данные представлены в таблице

Х (у.е.)	100	150	200	250	300
Y (чел.)	60	35	20	20	15

Найти линейную регрессию Y на Х и выборочный коэффициент корреляции.

88. При уровне значимости α=0.05 проверить гипотезу о нормальном распределении генеральной совокупности, если по выборке найдены эмпирические частоты 5, 13, 12, 44, 8, 12, 6 и рассчитаны теоретические (выравнивающие) частоты 2, 20, 12, 35, 15, 10, 6.