Понятие о проверке статистических гипотез о законе распределения генеральной совокупности

Пусть получено статистическое распределение выборки объема n :

xi	x1	x2	…	xk
ni	n1	n2	…	nk

По этим данным (например, исследуя форму гистограммы или по другим соображениям) выдвигается гипотеза о законе распределения генеральной совокупности (например, полагают, что она распределена по нормальному закону). Подобные гипотезы называются статистическими гипотезами. Затем по выборке вычисляются точечные оценки параметров предполагаемого распределения (например, для нормального распределения это будут выборочная дисперсия и выборочное среднее квадратическое отклонение). После этого для тех же объектов, которые попали в выборку, вычисляют новые частоты (они называются выравнивающими частотами и обозначаются ), исходя из предполагаемого закона распределения. Выравнивающие частоты при этом, вообще говоря, получаются отличными от наблюдаемых частот. Для решения вопроса о правильности выдвинутой гипотезы о законе распределения генеральной совокупности необходимо понять, является ли это различие случайным или оно обусловлено неправильностью выдвинутой гипотезы. Для ответа на этот вопрос применяют так называемыекритерии согласия эмпирических наблюдений выдвинутой гипотезе . Это, например, критерий χ² (читается «хи квадрат») Пирсона, критерии Колмогорова, Смирнова и т.д. . Здесь мы в качестве примера обсудим критерий χ² .

Предположим, что на основе опытных данных выдвинута гипотеза Н − генеральная совокупность распределена по нормальному закону. Для вычисления выравнивающих частот делают следующее:

• по статистическому распределению выборки находят выборочное среднее и выборочное среднее квадратическое отклонение;

• выравнивающие частоты находят по формуле .

В последней формуле n – объем выборки (равен сумме наблюдаемых частот), h – разность между двумя соседними вариантами, , а– так называемая функция Гаусса (она возникала в курсе теории вероятностей при расчетах в схеме Бернулли при большом числе испытаний, а таблица ее значений имеется в конце учебников по теории вероятностей и математической статистике). В результате получаем набор выравнивающих частот.

Обозначим через χ² сумму квадратов разностей между эмпирическими и выравнивающими частотами, деленных на соответствующие выравнивающие частоты:

.

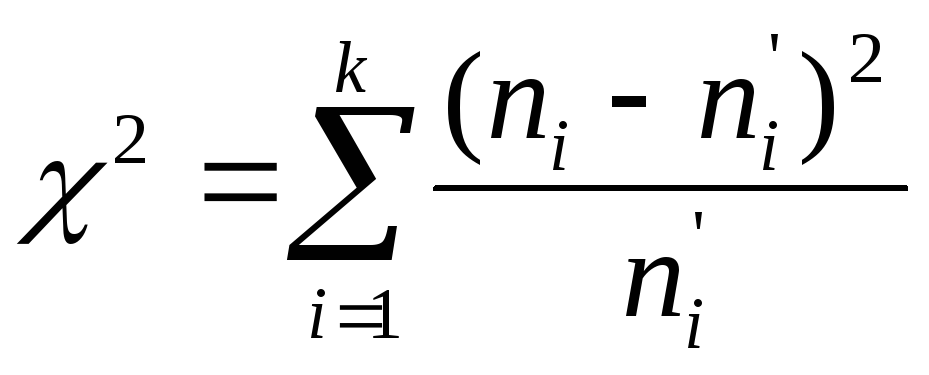Для данной выборки по этой формуле находим значение случайной (так как она зависит от выборки) величины χ², которое мы обозначим . Далее находим числоm = k −3 , называемое числом степеней свободы, где k − число различных вариант в выборке.

Далее проверка гипотезы Н проводится по следующей схеме. Задается доверительная вероятность γ ( 0.9, 0.95, 0.99 …) или уровень значимости α=1− γ (соответственно, 0.1, 0.05, 0.01 …) , при котором о событии , имеющем маленькую вероятностьα , можно с больной уверенностью сказать, что в единичном испытании (каковым являлось извлечение выборки) не произойдет. В таблице значений χ² (которая имеется в конце учебников по теории вероятностей и математической статистике) по заданному уровню значимости α и числу степеней свободы m находят значение χ²(α;m) . Если окажется, что , то гипотезаН отвергается на уровне доверительной вероятности γ (или на уровне значимости α=1− γ), так как произошло событие, которое с большой вероятностью γ не должно было произойти, если бы гипотеза Н была бы справедлива. Если же получилось , то гипотезаН принимается с данной доверительной вероятностью γ (или с данным уровнем значимости α=1− γ).

Пример. При уровне значимости α=0.05 проверить гипотезу о нормальном распределении генеральной совокупности, если по выборке найдены эмпирические частоты 6, 13, 38, 74, 106, 85, 30, 14 и рассчитаны теоретические (выравнивающие) частоты 3, 14, 42, 82, 99, 76, 37, 13.

Решение. Для данной выборки по приведенной выше формуле вычислим значение:. Найдем число степеней свободы, учитывая, что число различных вариантk=8 : m=8−3=5 . По уровню значимости α=0.05 и числу степеней свободы m=3 по таблице значений χ² находим: χ²(0.05;5)=11.1. Поскольку получилось, что χ²(0.05;5)> , то при данном уровне значимости нет оснований отвергнуть гипотезу о нормальном распределении генеральной совокупности.