Доверительные интервалы

Пусть по данным выборки { x₁, x₂, … , x_n } с.в. Х объема n , используя некоторую статистику

t_n = f (x₁, x₂, … , x_n) ,

получили статистическую оценку t_n параметра t всей случайной величины Х (т.е. всей генеральной совокупности). Если статистика обладает хорошими свойствами (из перечисленных выше), то мы вправе ожидать, что t_n ≈ t. Но хотелось бы дополнительно понять степень приближения. Насколько отличается t_n от t, т.е. чему равно отклонение | t_n−t| ? Возьмем, например, какое-нибудь маленькое число δ > 0 (0.1, 0.01 и т.п.) . Можно ли утверждать, что | t_n−t| < δ, т.е. истинный параметр t содержится в интервале (t_n− δ, t_n+ δ) ? Поскольку оценка t_n является значением соответствующей случайной величины T_n (т.е. зависит от выборки), то статистические методы дают вероятностный ответ на этот вопрос, т.е. позволяют определить вероятность γ, с которой это неравенство выполняется. Пусть t_n –полученная статистическая оценка параметра t . Интервал вида (t_n− δ, t_n+ δ) называется интервальной оценкой параметра t с доверительной вероятностью (или надежностью) γ, если с вероятностью γ этот интервал «покрывает» этот параметр ( t(t_n− δ, t_n+ δ) ), т.е. выполняется: Р(| T_n−t|< δ)= γ. Доверительную вероятность обычно берут на уровне 0.9, 0.95, 0.99 и т.п. . Число α=1− γ называется уровнем значимости интервальной оценки, оно показывает вероятность того, что параметр t выйдет за доверительный интервал: Р(| T_n−t|> δ)= α.

Доверительный интервал строится по следующей схеме. Сначала задается требуемый уровень значимости γ, по которому и подбирается число δ из условия, чтобы выполнялось Р(| T_n−t|< δ)= γ.

Конечно, нельзя утверждать, что найденный доверительный интервал обязательно покроет искомый параметр t. Но в этом можно быть уверенными на 95% при γ=0.95 и на 99% при γ=0.99 . Это значит, что если сделать много выборок (в идеале бесконечно много), то в 95% случаев (при γ=0.95) вычисленные доверительные интервалы действительно покроют параметр t.

Доверительный интервал для математического ожидания нормально распределенной генеральной совокупности при известном среднем квадратическом отклонении

Если речь идет, например, об измерении каких-нибудь величин одним прибором, то часто среднее квадратическое отклонение σ (ошибка измерения) бывает известна и не меняется от измерения к измерению.

Пусть с.в. Х распределена нормально с параметрами М(Х)=а и σ(Х)= σ, причем σ известно, а а нет. Требуется построить доверительный интервал для математического ожидания, покрывающий параметр а с заданной надежностью (т.е. доверительной вероятностью) γ . Пусть сделана выборка { x₁, x₂, … , x_n } с.в. Х объема n и по ней вычислено выборочное среднее

.

Как уже говорилось, полученная выборка есть реализация системы независимых случайных величин X₁, X₂, … , X_n , каждая из которых тоже имеет нормальное распределение с теми же параметрами а и σ . При этом вычисленное выше выборочное среднее есть реализация соответствующей случайной величины

.

Можно (но не так просто) доказать, что с.в. , определенная этой формулой, тоже распределена по нормальному закону. Используя свойства математического ожидания и дисперсии, легко найти параметры этого распределения:

.

Для построения доверительного интервала с заданной надежностью γ найдем такое δ, чтобы выполнялось неравенство . Для любой с.в.Х, распределенной по нормальному закону, ранее была выведена формула , гдеФ(х) – функция Лапласа. Применяя ее для нашего случая с полученными выше выражениями для математического ожидания и среднего квадратического отклонения, получим

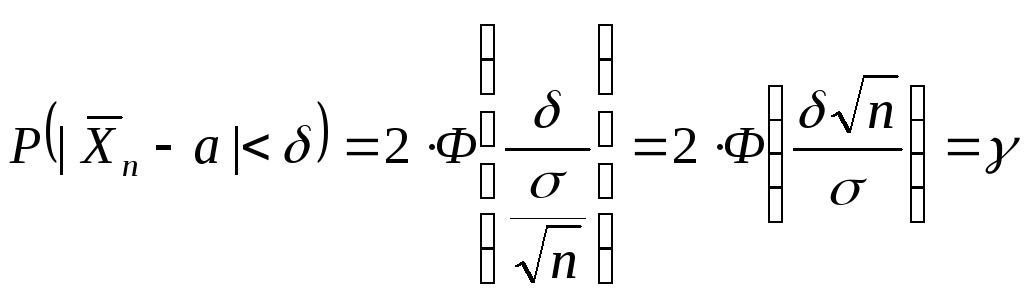
Поэтому искомое δ должно удовлетворять уравнению . Обозначим черезt такое число, что (такое число ищется из таблицы функции Лапласа). Тогдаδ должно удовлетворять уравнению , откуда. Таким образом, мы получили, что доверительный интервал

покрывает неизвестный параметр а с доверительной вероятностью γ , где − найденное по выборке выборочное среднее, а значение параметраt определяется из равенства по таблице значений функции Лапласа.

Пример. Генеральная совокупность некоторого признака Х распределена нормально с известным средним квадратическим отклонением σ=0.4 . Для определения среднего значения признака Х была сделана выборка объема n=20, по которой вычислено выборочное среднее . Найти доверительный интервал для математического ожиданияа признака Х с надежностью γ=0.99 .

Решение. Для находим по таблице функции Лапласа соответствующее значение параметраt=2.58 . Тогда по выписанной выше формуле с вероятностью γ=0.99 среднее значение а признака Х заключено в интервале .

Пример. Генеральная совокупность некоторого признака Х распределена нормально с известным средним квадратическим отклонением σ=3 . Для определения среднего значения признака Х была сделана выборка объема n=36, по которой вычислено выборочное среднее . Найти доверительный интервал для математического ожиданияа признака Х с надежностью γ=0.95 .

Ответ: 3.12<a<5.08 .