Свойства статистических оценок

Пусть статистическая оценка некоторого параметра t изучаемой с.в. Х выражена формулой (*) предыдущего параграфа : t_n = f (x₁, x₂, … , x_n) .

Оценка t_n параметра t в (*) называется несмещенной, если математическое ожидание соответствующей с.в. T_n в (**) равно оцениваемому параметру t : М(T_n)= t . Несмещенность оценки обеспечивает отсутствие систематического отклонения оценки t_n как в сторону завышения от t, так и в сторону занижения.

Разумно было бы также предположить, что с увеличением объема выборки n оценка t_n должна все ближе приближаться к оцениваемому параметру t . Но так как оценка t_n есть значение случайной величины T_n, то это требование должно выражаться на вероятностном языке. Оценка t_n в (*) параметра t называется состоятельной, если при n→∞ соответствующие случайные величины T_n в (**) сходятся по вероятности к t , т.е. для любого или, что то же самое,. Это означает, что при увеличении объема выборки вероятность того, что оценка мало отличается от истинного значения, приближается к1 ( т.е. при большом объеме выборки достаточно хорошее приближение t_n ≈ t практически достоверно). Часто состоятельность оценки помогает установить следующая

Теорема. Если оценка t_n параметра t является несмещенной, а дисперсия с.в. T_n стремится к 0 (т.е. ), то эта оценка является состоятельной.

Какие же еще свойства оценок (кроме несмещенности и состоятельности) желательны? Допустим, мы нашли две оценки (две статистики), обе несмещенные и состоятельные. Какую предпочесть? Естественно назвать более эффективной ту оценку, которая (как случайная величина) имеет меньшую дисперсию, т.е. в среднем меньше отклоняется от своего математического ожидания, коим (из несмещенности) является оцениваемый параметр . Хорошо бы найти самую эффективную оценку. Несмещенная оценка t_n в (*) называется эффективной, если соответствующая с.в. T_n в (**) имеет наименьшую дисперсию среди всех несмещенных оценок (при одном и том же объеме выборки n).

При изучении статистического распределения выборки мы уже проходили две статистические оценки. Пусть некоторый признак генеральной совокупности описывается с.в. Х с математическим ожиданием М(Х)=а и дисперсией D(X)=DX. По извлеченной выборке { x₁, x₂, … , x_n } мы строили точечные оценки этих параметров, которые называли выборочным средним и выборочной дисперсией:

.

Как и раньше, обозначим Х₁,Х₂, … ,Х_n − случайные величины, принимающие значения, которые с.в. Х приняла при получении выборки соответственно в 1-м испытании, …, n-м испытании. Как уже говорилось, каждая из них имеет то же самое математическое ожидание а и дисперсию DX, что и исходная с.в. Х. Тогда соответствующие этим статистическим оценкам (в смысле (**)) случайные величины имеют вид:

Теорема. Оценка является несмещенной и состоятельной оценкой математического ожиданияМ(Х).

Проще всего доказывается несмещенность. Используя свойства математического ожидания, получим

.

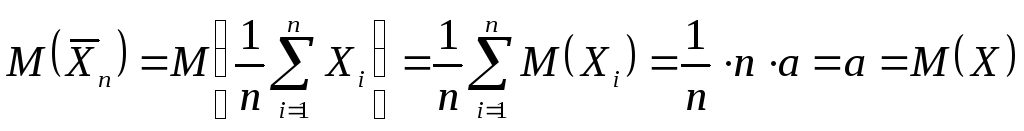Можно доказать, что эта оценка будет и эффективной, если с.в. Х распределена нормально.

Если, используя свойства математического ожидания, найти математическое ожидание для с.в. (которая соответствуетвыборочной дисперсии ), то можно получить, что. Таким образом,, а потомувыборочная дисперсия является смещенной (хотя и состоятельной) оценкой дисперсии. Поэтому выборочную дисперсию «исправляют», умножая на . Получаемая при этом оценка обозначается

и называется исправленной выборочной дисперсией. Из этой формулы легко получить выражение для исправленной дисперсии через параметры статистического распределения выборки:

.

Как видно из этих формул, при больших объемах выборки исправленная выборочная дисперсия мало отличается от выборочной дисперсии. Однако если объем выборки мал, то надо пользоваться именно исправленной выборочной дисперсией. На практике исправленной дисперсией пользуются, если примерно n < 30.

Теорема. Исправленная выборочная дисперсия есть несмещенная и состоятельная оценка дисперсии DX.

Корень из исправленной выборочной дисперсии обозначается S и называется исправленным выборочным средним квадратическим отклонением:

.

Отметим еще одно важное утверждение, которое оправдывает данное нами в курсе теории вероятностей статистическое определение вероятности произвольного события А как предела его относительной частоты W_n(A) при n→∞.

Теорема. Относительная частота W_n(A) появления события А в n независимых испытаниях является несмещенной, состоятельной и эффективной оценкой вероятности р=Р(А) этого события (в одном испытании).

Пример. Из 1500 деталей отобрали 250 . Дан интервальный ряд размеров отобранных деталей:

размер	7.8 − 8.0	8.0 − 8.2	8.2 − 8.4	8.4 − 8.6	8.6 − 8.8	8.8 − 9.0
количество	5	20	80	95	40	10

Оценить средний размер детали и соответствующую дисперсию.

Решение. Изучаемая н.с.в. Х − размер детали. Среднее значение этой с.в. и ее дисперсия оцениваются выборочным средним и исправленной выборочной дисперсией:

.

Поскольку задан интервальный (а не дискретный) ряд, то в качестве вариант {x_i} берутся середины соответствующих интервалов: 7.9, 8.1, … , 8.9 . Подставляя данные в выписанные формулы, получим ,.