
- •Содержание
- •Тема 2. Классические теоремы теории вероятностей
- •Если события а, в, с совместны, то
- •Формула полной вероятности имеет вид
- •Тема 3. Повторные независимые испытания
- •Тема 4. Случайные величины и законы их распределения
- •Тема 5. Числовые характеристики случайных величин
- •Пусть с – постоянная величина. Тогда
- •Для вычисления дисперсии используется формула
- •Дисперсия обладает свойствами
- •Тема 6. Основные дискретные случайные величины и их числовые характеристики
- •Если случайная величина распределена по закону Пуассона, то
- •Тема 7. Основные непрерывные случайные величины и их числовые характеристики
- •Плотность нормального распределения имеет вид
- •Дисперсия нормального распределения
- •Правило трех сигм записывается в виде равенства
- •2. Для нахождения математического ожидания и дисперсии применим формулы (7.3). Получим следующие значения:
- •Ошибка указания времени часами со скачущей минутной стрелкой имеет равномерное распределение. Определить вероятность того, что при определении времени ошибка не будет превышать 20 секунд.
- •Тема 8. Закон больших чисел и центральная предельная теорема
- •В предельной форме утверждения теоремы Бернулли имеют вид
- •Тема 9. Основные понятия математической статистики. Числовые характеристики
- •На практике для вычисления дисперсии применяется формула
- •Легко установить, что
- •Вычислим размах товарооборота по формуле (9.14). Получим, что
- •Тема 10. Статистические оценки
- •Если дисперсия несмещенной оценки при n→стремится к нулю, то такая оценка будет и состоятельной. Это следует из неравенства Чебышева (см.(8.2))Рдля случайной величины*.
- •Тема 11. Корреляция и регрессия
- •Непосредственно из этого определения следует, что
- •Тема 12. Проверка статистических гипотез
Тема 4. Случайные величины и законы их распределения
Понятие случайной величины. Дискретные и непрерывные случайные величины. Примеры случайных величин. Закон распределения случайной величины. Ряд распределения дискретной случайной величины. Многоугольник распределения (полигон). Функция F(х) распределения случайной величины (интегральная функция) и ее свойства. Вид функции F(х) для дискретной случайной величины. Графики функции F(х) для дискретных и непрерывных случайных величин. Плотность вероятности (дифференциальная функция f(х)) и ее свойства. Вероятностный смысл дифференциальной функции. Связь между дифференциальной и интегральной функциями. Вероятность попадания непрерывной случайной величины в заданный промежуток.
Л и т е р а т у р а
[2], гл. 3, § 1, 2; [3], гл.5, 5.1-5.4; [5], гл.6, § 1-3, гл.10, § 1-3, гл.11, § 1-5; [6], гл.4, § 18,19; [7], гл.7, § 18,19, гл.12, § 29, 30; [8], гл.3, § 1, гл.4, § 1-3; [9], гл.2, § 1, гл.3, § 1-4; [10], гл.3, § 1, 2; [11], гл.29, § 196-198; [12], гл.3, § 9; [13], гл.20, § 7, § 12, 13; [14], § 1; [15], гл.5, § 1-3; [16], гл.2, 2.1, 2.2.1-2.2.3, 2.6.1.
О с н о в н ы е п о л о ж е н и я и ф о р м у л ы
Рассмотрим событие Х< х, состоящее в том, что случайная величина Х примет какое-нибудь значение, меньше произвольного числа х. Функция F(х), определенная равенством
F(х) = Р (Х< х), (4.1)
называется функцией распределения вероятностей случайной величины Х. Она обладает следующими свойствами:
1) 0 F(х) 1 (4.2)
2) F(х2) F(х1) , если х2 > х1 ; (4.3)
3)
F(-)
=
![]() F(х)
= 0, F(+)
=
F(х)
= 0, F(+)
=
![]() (4.4)
(4.4)
Для дискретной случайной величины (хi, рi) функция F(х) имеет вид
F(х)
Р
(Х <
х)
=
![]() ,
рi
= P(Х=хi).
(4.5)
,
рi
= P(Х=хi).
(4.5)
Так, для дискретной случайной величины с конечным множеством значений (i=1, …, n) F(х) имеет следующий вид:
F(х)
=
 (4.6)
(4.6)
Для непрерывной случайной величины плотность распределения вероятностей f(х) в точке х определяется равенством
F(х)
=
![]() ,
(4.7)
,
(4.7)
где х < Х < х+х – событие, состоящее в том, что случайная величина примет значение, принадлежащее интервалу (х, х+х) длины х. Так как Р(х < Х < х+х) = F(х+х) – F(х), то в точках существования произвольной функции F(х) имеет место равенство
f(х) = F’(х). (4.8)
Поэтому плотность часто называют дифференциальной функцией.
Плотность распределения вероятностей обладает следующими свойствами:
1) f(х) 0,
2)
![]() f(х)
dx
= 1.
(4.9)
f(х)
dx
= 1.
(4.9)
Если плотность f(х) интегрируема, то можно найти функцию распределения F(х) по формуле
F(х)
=
![]() .
(4.10)
.
(4.10)
Вот почему функцию распределения часто называют интегральной функцией.
Если известна функция F(х), то вероятность попадания случайной величины на полуотрезок [а, b) находится по формуле
Р(а Х < b) = F(b) – F(а). (4.11)
Если известна плотность f(х) и она интегрируема на промежутке <a, b> (интервале, отрезке, любом полуотрезке), то
Р(а<Х<b)
=
![]() .
(4.12)
.
(4.12)
Р е ш е н и е т и п о в ы х з а д а ч
Задача 1. В группе 25 студентов. По результатам экзаменационной сессии 18 студентов получают стипендию, причем 6 из них – повышенную. Построить ряд распределения и полигон величины стипендии для наудачу выбранного студента этой группы, если размер обычной стипендии составляет 200 рублей, а повышенной – 250 рублей.
Решение. Случайная величина Х (величина стипендии) может принимать следующие значения: х1=0, х2=200, х3=250. Вероятности этих возможных значений соответственно равны: р1=7/25, р2=12/25, р3=6/25. Поэтому закон (ряд) распределения случайной величины Х имеет вид
|
Х |
0 |
200 |
250 |
|
Р |
7/25 |
12/25 |
6/25 |
Полигон построить самостоятельно.
Задача 2. Составить функцию распределения и построить ее график для дискретной случайной величины Х, заданной законом распределения
|
Х |
1 |
3 |
4 |
7 |
|
Р |
0,2 |
0,1 |
0,4 |
0,3 |
Решение.
Составим функцию распределения F(х).
Если х
1, то F(х)=Р(Х<х)=0.
Если 1<
х
3, то F(х)=Р(Х<х)=![]() Р(Х=хi)=Р(Х=1)=0,2.
Если 3 <
х
4, то F(х)=Р(Х<х)=
Р(Х=хi)=Р(Х=1)=0,2.
Если 3 <
х
4, то F(х)=Р(Х<х)=
![]() Р(Х=хi)=Р(Х=1)+Р(Х=3)=0,2+0,1=0,3.
Если 4<
х
7, то F(х)=Р(Х=1)+Р(Х=3)+Р(Х=4)=0,7.
Если х>7,
то F(х)=Р(Х=1)+Р(Х=3)+Р(Х=4)+Р(Х=7)=1.Следовательно,
F(х)
имеет вид
Р(Х=хi)=Р(Х=1)+Р(Х=3)=0,2+0,1=0,3.
Если 4<
х
7, то F(х)=Р(Х=1)+Р(Х=3)+Р(Х=4)=0,7.
Если х>7,
то F(х)=Р(Х=1)+Р(Х=3)+Р(Х=4)+Р(Х=7)=1.Следовательно,
F(х)
имеет вид
F(х)
=

Составленную функцию распределения изобразим графически:
 y
y

х
Величины скачков в точках разрыва х=1, х=3, х=4, х=7 как раз равны вероятностям, что случайная величина Х примет эти значения.
Задача 3. Функция распределения непрерывной величины Х задана выражением
F(х)
=
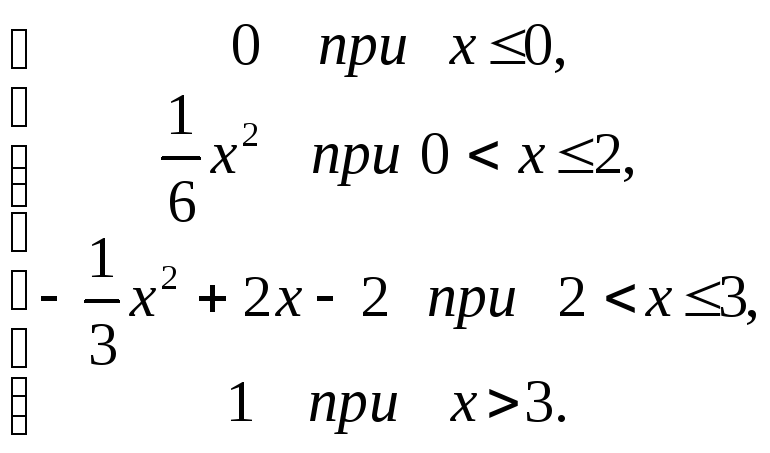
Построить график этой функции. Найти вероятность попадания случайной величины на интервал (1; 2,5).
Решение. График функции изображен ниже на рисунке.
 y
y
 0
х
0
х
При 0 < х 2 графиком функции является часть параболы. Ветви параболы направлены вверх, а вершина находится в начале координат. При 2 < х 3 график функции представляет собой часть параболы, вершина которой находится в точке (3; 1), а ветви направлены вниз. Для х0 и х>3 графиком функции F(х) являются прямые y=0 и y=1.
По формуле (4.11) находим, что
Р(1<Х<2,5)
= F(2,5)
– F(1)
=
![]()
Задача 4. Функция
f(х)
=

служит
плотностью вероятностей случайной
величины Х.
Найти коэффициент А. Вычислить вероятность
того, что случайная величина Х
примет какое-нибудь значение из отрезка
![]() .
.
Решение. Используя равенство 2) из (4.9), получим
![]()
Следовательно,
f(х)
=

Для
вычисления Р(0Х![]() )
применим формулу (4.12). Получим
)
применим формулу (4.12). Получим
Р
(0
Х
![]() )
=
)
=![]()
Задача 5. Дана функция распределения F(х) случайной величины Х:
F(х)
=
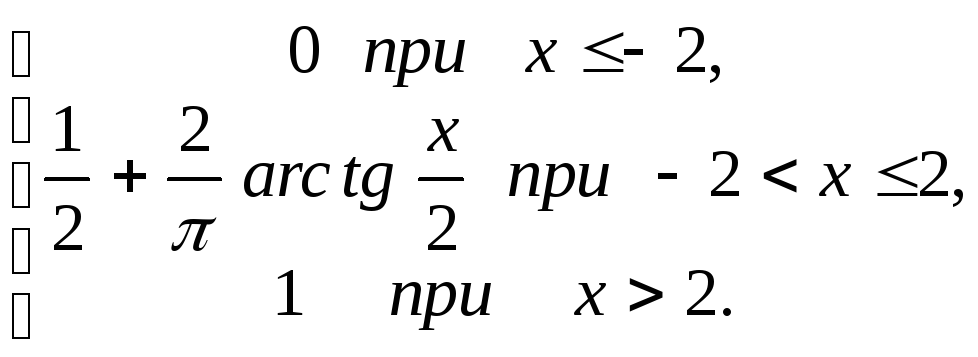
Определить: 1) плотность вероятности f(х), 2) вероятность того, что случайная величина примет значение в промежутке [0; 2].
Решение. 1. Определяем плотность распределения. Так как плотность вероятности есть производная от функции распределения (см.(4.8)), то вне интервала (-2; 2) плотность вероятности равна нулю. Найдем плотность вероятности для всех х, принадлежащих интервалу
(-2;2):
f(х)
= F(х)
=

Таким образом, искомая плотность имеет вид:
f(х)
=

2. Вероятность того, что случайная величина примет значение на отрезке [0; 2], равна приращению интегральной функции распределения на этом промежутке (см.(4.11)). Следовательно,
Р(0Х2)
= F(2) – F(0)
=
![]()
Тогда искомая вероятность Р(0Х2) = 0,5.
Задача 6. Найти функцию распределения непрерывной случайной величины, плотность распределения вероятностей которой задана функцией
f(х)
=

Решение.
Применяя формулу (4.10), найдем функцию
распределения. Если х
![]() ,
тоF(х)
= 0, так как f(х)=0
в этом промежутке. Если
,
тоF(х)
= 0, так как f(х)=0
в этом промежутке. Если
![]() ,
тоF(х)=
,
тоF(х)=![]() Еслих>
Еслих>![]() ,
то
,
то
F(х)=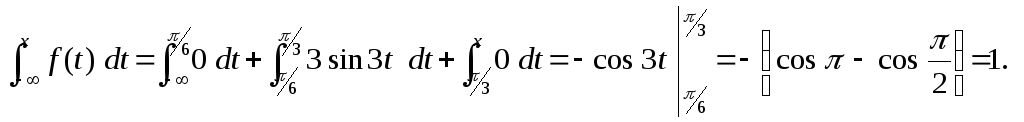
Таким образом,
F(х)
=

З а д а ч и
Выпущено 1 000 билетов денежной лотереи. При этом разыгрываются один выигрыш в 1 000 рублей, пять выигрышей по 500 рублей, двадцать выигрышей по 50 рублей. Составить ряд распределения стоимости выигрыша для владельца одного лотерейного билета. Построить полигон распределения. Найти функцию F(х) и построить ее график.
Монета брошена 4 раза. Составить ряд распределения случайной величины Х – частоты появления герба. Построить полигон распределения. Найти функцию F(х) и построить ее график.
Составить закон распределения случайного числа попадания кольца на колышек при одном броске, если вероятность попадания кольца на колышек у игрока равна 0,7. Указать функцию F(х) и построить ее график.
Рабочий обслуживает три станка. Вероятность того, что в течение часа первый станок потребует внимания рабочего, равна 0,15; для второго и третьего станков эти вероятности равны, соответственно, 0,2 и 0,25. Составить ряд распределения числа станков, которые потребуют внимания рабочего в течение часа.
Охотник, имеющий 4 патрона, стреляет в цель одиночными выстрелами до первого попадания или пока не израсходует все патроны. Составить ряд распределения случайной величины Х – количества израсходованных патронов, если вероятность попадания при каждом выстреле равна 0,6.
Вероятность изготовления нестандартного изделия при производстве некоторой продукции составляет 5%. Для проверки качества изделий контролер из всей партии случайно выбрал 5 изделий и должен проверять их до обнаружения нестандартного. Составить закон распределения числа изделий, проверяемых контролером.
В партии из восьми деталей пять стандартных. Наудачу отбираются три детали. Составить закон распределения числа стандартных деталей среди отобранных.
Построить график функции распределения
F(х)
=

Найти плотность распределения вероятностей и построить ее график. Вычислить вероятность попадания случайной величины в интервал (0, 1).
Функция распределения непрерывной величины Х задана выражением
F(х)
=

Найти плотность вероятности f(х) и построить ее график.
Случайная величина Х распределена по закону Коши: f(х)=
 .
Найти: 1) коэффициент А; 2) функцию
распределенияF(х);
3) построить графики f(х)
и F(х);
4) вероятность попадания величины Х
на интервал
.
Найти: 1) коэффициент А; 2) функцию
распределенияF(х);
3) построить графики f(х)
и F(х);
4) вероятность попадания величины Х
на интервал
 .
.Дана плотность вероятности случайной величины:
f(х)
=

Требуется: 1) найти функцию распределения; 2) построить графики функций f(х) и F(х); 3) вычислить вероятность того, что значение случайной величины будет находиться в интервале (2; 5).
