Тема 6. Основные дискретные случайные величины и их числовые характеристики

Равномерное дискретное распределение. Гипергеометрическое распределение. Биномиальное распределение. Геометрическое распределение. Распределение Пуассона. Относительная частота события как случайная величина.

Л и т е р а т у р а

[2], гл.3, § 1, 2, гл.4, § 1,5; [3], гл.5, 5.9, гл.10, 10.3; [5], гл.6, § 4-6, гл.7, § 5, гл.8, § 6; [6], гл.4, § 18, гл.5, § 23; [8], гл.3, § 1,5; [9], гл.2, § 2, 3, 7; [11], гл.29, § 203, 206; [12], ч.2, гл.3, § 11; [13], гл.20, § 8, [14], § 3, 3.1-3.6; [15], гл.6, § 1-3; [16], гл.2, 2.3-2.5.

О с н о в н ы е п о л о ж е н и я и ф о р м у л ы

Пусть {х₁, …, х₂} – множество значений случайной величины Х, принимающей n значений. Распределение такой дискретной случайной величины называется равномерным, если вероятности появления значений определяются формулой:

Р(Х=х_i) = (i=1,…, n). (6.1)

Функция распределения этой случайной величины Х имеет вид

F(х) =

График функции представляет собой ступенчатую линию со скачками в точках х=х_i (i=1,…,n). Величина скачка в каждой точке равна 1/n. Математическое ожидание и дисперсия равномерно распределенной дискретной случайной величины могут быть найдены по формулам

М(Х) = , (6.3)

Д(Х) = . (6.4)

Пусть n – число различных элементов некоторого множества, из которых s элементов обладают определенным свойством. Из всего множества производится выборка без возвращения объема k. Пусть m – число элементов, обладающих этим же свойством и оказавшихся в выборке, причем m может принимать значения m=0, 1, …, s, если s  k. Случайная величина Х называется гипергеометрически распределенной, если вероятности появления ее значений находятся по формуле

Р(Х=m) = . (6.5)

Значения m определяются смыслом формулы (6.5) для каждой конкретной задачи. Для математического ожидания и дисперсии гипергеометрического распределения справедливы соотношения

М(Х) = k,Д(Х) = k. (6.6)

Пусть Х – случайная величина, значениями которой являются возможные значения числа m появления события А при проведении n повторных независимых испытаний, в каждом из которых вероятность появления А постоянна и равна р. В зависимости от случая m может принимать все целочисленные значения от 0 до n включительно. Вероятности принятия этих значений находятся по формуле Бернулли

Р(Х=m)Р_n(m)=. (6.7)

Такое дискретное распределение называется биномиальным. Функция F(х) этого распределения имеет следующий вид:

F(х) = (6.8)

Суммирование здесь ведется по всем целым числам m, меньшим х. График функции распределения представляет собой ступенчатую линию со скачками в точках х=0, 1, …, n. Величина скачка в точке х=m равна Р_n(m). Для биномиально распределенной случайной величины числовые характеристики находятся по формулам

М(Х) = np, Д(Х) = np (1-р). (6.9)

Пусть Х – случайная величина, значениями которой являются возможные значения числа m проведенных испытаний, удовлетворяющих схеме Бернулли, причем опыт прекращается после первого же испытания, в котором рассматриваемое событие появилось. Геометрическое распределение вероятностей задается формулой

Р(Х=m) = р (1-р)^m-1 (m=1, 2, 3, …). (6.10)

Функция распределения F(х) имеет вид

F(х) = (6.11)

Если случайная величина Х имеет геометрическое распределение, то

М(Х) = ,Д(Х) = . (6.12)

Пусть случайная величина Х принимает целые неотрицательные значения m=0, 1, 2, …с вероятностями

Р(Х=m) = (6.13)

Такое дискретное распределение называется распределением Пуассона с параметром . При различных  получим различные распределения. Функция F(х) этого распределения имеет вид

F(х) = 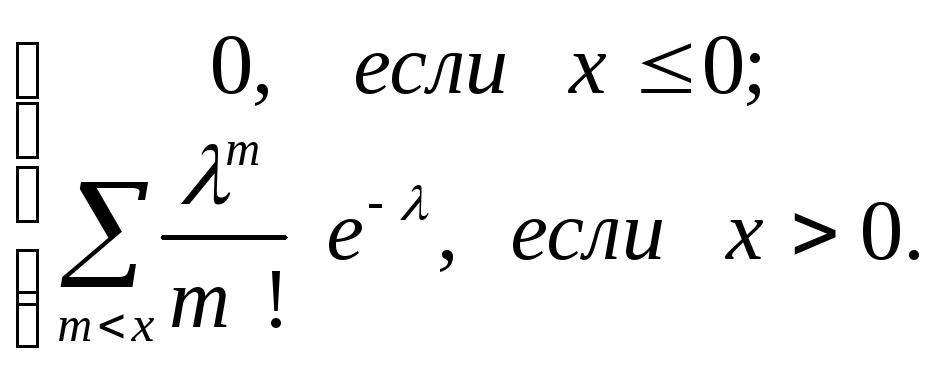(6.14)