матан 3 курс 2013 / лекции / Oglobina

10

Наприклад, y = x2 + 2x + 4 . y – залежна змінна, х – незалежна

або аргумент.

Функція називається заданою неявно, якщо вона задається рівнянням, нерозв’язаним відносно залежної змінної:

F (x, y) = 0 .

(5)

Наприклад, F (x, y) = x2 + xy + y3 = 0 - незалежна змінна х та залежна змінна у входять в один аналітичний вираз.

2. Обернена функція.

Нехай y = f (x) – функція від незалежної змінної x , X – ОВФ, Y – ОЗФ.

Означення 2

Якщо можна кожному значенню y Y поставити у відповідність єдине значення x X , для якого y = f (x), то кажуть, що існує функція x = ϕ(y) – обернена до y = f (x).

Позначають обернену функцію x = f −1 (y).

Наприклад, y = a x та x = loga y – взаємно обернені функції.

Можна довести, що для будьякої строго монотонної функції існує обернена.

3. Складена функція.

Означення 3

Нехай функція y = f (u) – є функція від змінної u з ОВФ U та ОЗФ Y , а u , в свою чергу є u = ϕ(x) з ОВФ X та ОЗФ U . Функція

y = f (ϕ(x))

називається складеною функцією від незалежної змінної х (або

суперпозицією, композицією функцій).

Наприклад, y = arctg5 (ln3x). Тут функція y є композицією чотирьох функцій

11

y = s5 ; s = arctg v; v = ln u; u = 3x .

4. Основні елементарні функції. Степенева функція

y = xn , n - дійсне число.

Показникова функція y = a x , a > 0, a ¹ 1 .

Експоненціальна функція (показникова з основою е) y = e x , e = 2,718281828 .

Логарифмічна функція (обернена до показникової)

y = loga x,		a > 0,		a ¹ 1
y = ln x a = e.
Тригонометричні функції
y = sin x;				y = cos x;
y = tg x;				y = ctg x;
y = sec x =		1	;	y = cos ecx =	1	.
	cos x
					sin x
Обернені тригонометричні функції
y = arcsin x;				y = arccos x;
y = arctg x;				y = arcctg x;
y = arc sec x;				y = arccos ec x.

5. Елементарні функції.

Означення 4

Функції, які побудовані з основних елементарних функцій скінченою множиною алгебраїчних перетворень та скінченою кількістю операцій називаються елементарними.

		x	+ sin 3x
Наприклад, функція y =				- 7 (x + 5)3 - елементар-
			2
	5 x		+ ln x
на функція.

12

6. Класифікація елементарних функцій.

Елементарні функції діляться на алгебраїчні та неалгебраї-

чні (трансцендентні).

Алгебраїчні функції:

а) ціла раціональна функція (поліном)

y = P (x) = a

xn + a

n −1

xn−1

+ ... + a x + a

– поліном n -го степе-

n

n

1

0

ня.

y = P (x) = 3x5 + 2x3 − 7x2

+ 4 – поліном 4-го сте-

Наприклад,

5

пеня. Тут a5 = 3,

a4 = 0, a3 = 2, a2 = −7, a1 = 0, a0 = 4 ,

ai Z, i =

х –

незалежна змінна;

1,5

б) дробово-раціональна функція –

відношення поліномів

y =

Pn (x)

Qm (x)

.

P0

(x)

5

Наприклад, y =

(x)

=

;

Q

x3 − 8

3

в) ірраціональна функція – уфункції присутнє добування кореня з аргументу.

Наприклад, y = 3 x + y − x − 4 y .

6 x

Будь яка неалгебраїчна функція називається трансцендент- ною. До трансцендентних функцій відносяться такі функції:

-показникові;

-логарифмічні;

-тригонометричні;

-обернені тригонометричні.

13

§2 ГРАНИЦЯ ФУНКЦІЇ

2.1ГРАНИЦЯ ПОСЛІДОВНОСТІ Й ФУНКЦІЇ. ТЕОРЕМИ ПРО ГРАНИЦІ

2.1.1ГРАНИЦЯ ПОСЛІДОВНОСТІ. ГЕОМЕТРИЧНИЙ ЗМІСТ

ГРАНИЦІ ПОСЛІДОВНОСТІ

Означення

Число A називається границею послідовності {xn }∞n=1 , якщо для будь-якого достатньо малого позитивного числа ε існує номер N ( N = N (ε) ) такий, що всі значення xn , у яких n > N , за-

довольняють нерівність:
	xn − A		< ε .	(2.1)
Записують це в такий спосіб: lim xn = A або xn → A .
			n→∞
Геометричний зміст границі послідовності:
нерівність (2.1) рівносильна подвійній нерівності
	A − ε < xn < A + ε .			(2.2)
Це означає, що всі точки xn , починаючи з деякого номера
n > N , лежать усередині інтервалу (A − ε, A + ε)				на числовій

прямій, тобто попадають у будь -який достатньо малий ε - окіл точки A .

2ε

A-ε

a7

a8

A+ε

a1

a3

a5

A a6

a4 a2 an

Рисунок 2.1 Послідовність, яка має скінчену границю, називається збіж-

ною, у протилежному випадку – розбіжною.

Використовуючи символи логічного запису, означення границі можна записати так:

14

(A = lim xn ) (ε > 0)( N = N (ε))( n > N )

xn − A

< ε . (2.3)

n→∞

Приклад

На основі означення довести, що границя послідовності

3

2

5

(− 1)

n

0,

,

,

, ..., 1 +

, ...

дорівнює 1.

2

3

4

n

Доведення

Якщо 1 є границею даної послідовності, то за означенням

(− 1)

n

lim

1

+

− 1

< ε .

n→∞

n

Нехай ε = 0,1 .

n

n

Тоді lim

1 +

(− 1)

− 1

< 0,1 , або lim

(− 1)

< 0,1, що означає

n→∞

n

n→∞

n

1

<

1

.

n

10

нерівність буде виконуватися для n > 10 . Знайшли

Отже,

N = 10 , починаючи з якого нерівність виконується.

n

Нехай

ε = 0,001 .

Тоді

lim

1 +

(− 1)

− 1

< 0,001 ,

або

n→∞

n

(− 1)n

lim

< 0,001 , що означає

1

<

1

n

1000

n→∞

n

Отже,

нерівність буде виконуватися для n > 1000 . Знайшли

N = 1000 , починаючи з якого нерівність виконується.

Залежно від ε > 0 ми знаходимо такий номер N = N (ε),

що

для всіх n , більших за цей номер, нерівність (2.1) виконується завжди.

Тобто доведено, що 1 дійсно є границею даної послідовності.

15

2.1.2 ГРАНИЦЯ ФУНКЦІЇ НА БЕЗКІНЕЧНОСТІ

Поняття границі функції на безкінечності є узагальненням поняття границі послідовності, тому що послідовність можна розглядати як функцію xn = f (n) цілого аргументу n , n → ∞ .

Означення

Число A називається границею функції y = f (x), x R за умови x → ∞ , якщо для будь-якого достатньо малого позитивного числа ε знайдеться таке число S > 0 (залежно від ε : S = S(ε) ), що для всіх x > S виконується нерівність

	f (x) − A		< ε .	(2.4)
Записують цей факт у такий спосіб:
lim f (x) = A, або				f (x)¾¾¾® A .
x→∞				x→∞

Формальний запис означення границі функції на безкінечності

(A = lim f ( x ))Û ("e > 0)($S = S (e))("x : x > S ) f ( x ) - A < e .(2.5)

x →∞

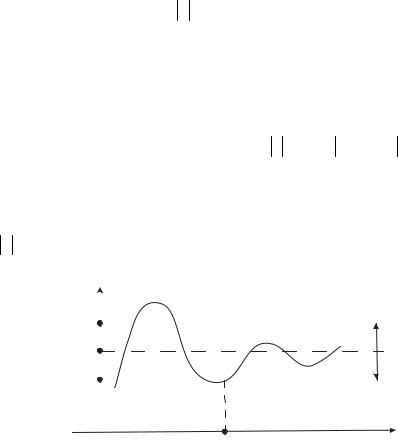
Геометричний зміст границі функції на безкінечності:

нерівність (2.4) можна записати	- ε + A < f (x) < ε + A .
Це означає, що з деякого	x = S для значень аргументу

x > S графік функції вміщується у смугу розміром 2ε , якою б вузькою ця смуга не була.

y
A+ε	y=f (x)
A		2ε
A-ε
0	S	x
	Рисунок 2.2

16

2.1.3 ГРАНИЦЯ ФУНКЦІЇ В ТОЧЦІ

Нехай дана функція f (x) і нехай A – гранична точка області визначення цієї функції D( f ) , тобто така точка, будь-який окіл якої містить точки множини D( f ) , відмінні від A . Точка A може належати множині D( f ) , а може й не належати їй.

Означення 1 (означення границі по Гейне – мовою послідовно- стей)

Число A називається границею функції f (x) при x → a ,

якщо для множини послідовностей {xn}∞n =1 значень аргументу, кожна з яких прямує до a , відповідні їм послідовності значень

функції {f (xn )}∞n=1 мають одну й ту саму границю – A .

Означення 2 (означення границі за Коши – мовою ε − δ )

Число A називається границею функції f (x) при x → a , якщо для заданого довільного будь-якого достатньо малого числа ε > 0 , можна знайти таке δ > 0 (δ = δ(ε)) , що для всіх x , з δ

– околу числа a , значення функції								f (x) будуть лежати в ε –
околі числа A , тобто для всіх x таких, що:
0 <			x - a				< δ ,	(2.6)
виконується нерівність
	f (x) - A						< ε .	(2.7)

Означення 1 і 2 рівносильні. Записують факт існування границі так:

lim f (x) = A, або f (x) ¾¾¾® A .		(2.8)
x→a	x →a

Формальний запис означення границі функції в точці:

(A = lim f (x)) Û

x → a

Û ("e > 0)($d = d(e) > 0)("x ¹ a : x - a < d) f ( x ) - A < e . (2.9)

17

Геометричний зміст границі функції в точці.

Нерівність (2.7) можна записати − ε + A < f (x) < ε + A , що від-

повідає вміщенню графіка у смугу, завширшки у 2ε , якою вузькою ця смуга не була б. Нерівність (2.6) теж можна записати як подвійну: − δ + a < x < δ + a , що також означає смугу завширшки у 2δ навколо точки a .

Число A є границею функції	f (x)	за x → a ,	якщо для
будь якого малого ε > 0 знайдеться	δ –	окіл точки	a(δ = δ(ε))

такий, що для всіх абсцис x ¹ a з цього околу ординати графі-

ка

функції

y = f (x)

будуть

вміщені

в

смугу

− ε + A < f (x) < ε + A , якою вузькою вона не була б.

y

y=f (x)

A+ε

2ε

A

A-ε

δ

δ

x -δ

x +δ

x

0

x0

0

0

Рисунок 2.3

Означення 3

У тому випадку, якщо послідовність {f (xn )}∞n=1 необмежено

зростає (або спадає) при будь-якому способі наближення

x до

своєї граничної точки a , будемо говорити, що функція

f (x)

має нескінченну границю, і записувати це у вигляді:

lim f (x) = ∞ , або lim f (x) = −∞ .

(2.10)

x

→ a

x →a

18

2.1.4 ОДНОБІЧНІ ТА НЕСКІНЧЕННІ ГРАНИЦІ ФУНКЦІЇ В ТОЧЦІ

Розглянемо поведінку функції, коли аргумент прямує до своєї граничної точки або ліворуч, або праворуч. Позначають таке прямування аргументу так

прямування ліворуч –		x → a−0 ,
прямування праворуч –		x → a+0 .
Означення	скінчена границя функції y = f (x) за умо-
Якщо число A –
ви, що аргумент x	прямує до граничної точки a ліворуч

x → a−0 , то така границя називається лівою границею функції y = f (x) у точці a і позначається:

lim	f (x) = A .	(2.11)
x→a−0
Якщо число A –		скінчена границя функції y = f (x) за умо-
ви, що	аргумент x	прямує до граничної точки a праворуч

x → a+0 , то така границя називається правою границею функ-

ції y = f (x) в точці a і позначається:
lim f (x) = A .	(2.12)
x→a+0

Загальна назва таких границь – однобічні границі.

Теорема

Для існування границі функції y = f (x) у точці a необхідно

і достатньо, щоб однобічні границі цієї функції в точці a існували і були рівні між собою:

lim	f (x) = lim f (x) = A .
x→a−0	x→a+0

19

2.1.5 НЕСКІНЧЕННО МАЛІ ТА НЕСКІНЧЕННО ВЕЛИКІ ВЕЛИЧИНИ

Означення 1

Функція α(x) називається нескінченно малою функцією при x → x0 , якщо

lim α (x) = 0 .

x→x0

Нехай α(x) та β(x)	– нескінченно малі при x → x0 . Якщо
існує границя їх частки	lim	α (x) = A , то розглядають три типи
	x→x0	β (x)

відношення безкінечно малих величин α(x) і β(x).

1. А є скінченою величиною, A ¹ 0 , тоді α(x) і β(x) нази-

вають нескінченно малими величинами одного порядку ма-

лості для x → x0 .

Якщо A = 1 , то α(x) і β(x) є еквівалентними нескінченно малими величинами для x → x0 . Позначається цей факт

α(x) ~ β(x).

2. A = 0 – функція α(x) називається нескінченно малою величиною вищого порядку малості відносно β(x) для

x→ x0 .

3.A = ¥ – функція α(x) називається нескінченно малою

величиною нижчого порядку малості відносно β(x) для x → x0 .

Означення 2

Функція Ω(x) називається нескінченно великою при x → x0 , якщо

lim Ω(x) = ∞ .

x→x0