матан 3 курс 2013 / лекции / Oglobina

50

y

C

y=f (x)

sup f (x)

= C

[a,b]

C = f (c)

a < c < b

0

a

c b

x

Рисунок 3.3 – Теорема Ферма

Теорема Ролля

Нехай функція y = f (x) задовольняє таким умовам:

1.Неперервна на замкненому інтервалі [a,b].

2.Диференційована на відкритому інтервалі (a,b).

3.На кінцях інтервалу набуває рівні значення f (a) = f (b) . Тоді всередині інтервалу існує хоча б одна точка x0 , в якій

похідна від функції дорівнює 0

f ′(x0 ) = 0 .

y

A

y=f (x)

f (a) = f (b) = A

f ′(x1 ) = 0; f ′(x2 ) = 0

x1, x2 [a,b]

0 a x

1

x2 b x

Рисунок 3.4 – Теорема Ролля Теорема Ролля є частинним випадком теореми Лагранжа.

51

Теорема Лагранжа (про скінчений приріст функції)

Якщо функція y = f (x) неперервна на інтервалі замкненому [a,b] і має похідну в кожній точці відкритого інтервалу (a, b), то у середині цього інтервалу існує хоча б одна точка ξ (a < ξ < b) така, що виконується рівність

	f (b)− f (a)	= f ′(ξ),		(3.18)
	b − a
або
	f (b)− f (a) = f ′(ξ)(b − a).			(3.18*)
Формулу (3.14) називають формулою Лагранжа.
Механічний зміст теореми Лагранжа
	f (b)− f (a)		– зміна функції на інтервалі [a,b];
	f (b) − f (a)		- середня швидкість зміни функції на [a,b];
	b − a

y′ - це миттєва швидкість зміни функції в точках інтервалу

[a,b].

Отже, теорема Лагранжа стверджує, що всередині інтерва-

лу [a,b] існує хоча б одна точка c , миттєва швидкість зміни функції в якій дорівнює середній швидкості зміни функції на

цьому інтервалі.
Геометричний зміст теореми Лагранжа.
Якщо через точки графіка			A = f (a) та	B = f (b) провести
січну AB , то її кутовий			коефіцієнт	буде дорівнювати
k =	f (b) − f (a)	.
	b − a

Будемо зміщати січну паралельно собі самій до тих пір, доки вона не перетвориться на дотичну в деякій точці x0 . Коефіцієнт

дотичної в точці x0 , як відомо, дорівнює k = y′(x0 ) . З іншого боку, оскільки ми переміщували січну паралельно собі самій, то

52

кутовий коефіцієнт її залишився рівним k =			f (b) − f (a)		. Отже,
			b − a
якщо така точка x0	існує, то в ній y′(x0 ) =	f (b) − f (a)		.
			b − a

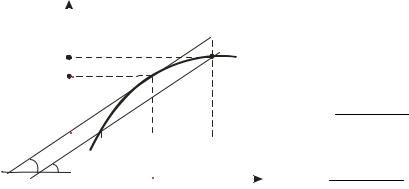
Теорема Лагранжа твердить, що така точка існує.

y
f (b)	y=f (x)
f (ξ)

f (a)

l1 α	α
l	0	a		ξ		b x

l : tg

α = f (b) − f (a)

b − a l1 : tgα = f ′(ξ)

f ′(ξ) = f (b)− f (a)

b − a

Рисунок 3.5 – Теорема Лагранжа

Слідство з теореми Лагранжа

Якщо похідна функції y = f (x) дорівнює нулю на деякому інтервалі [a,b], то функція на цьому інтервалі тотожно стала.

Правило Лопіталя

Теорема

Границя відношення двох нескінченно малих або двох нескінченно великих дорівнює границі відношення їх похідних (скінченій або нескінченній) якщо така границя існує.

Отже,

1) якщо lim				f (x) = 0 та lim g(x) = 0,
	x→x0								x→x0
	(x→∞ )								(x→∞ )
x→ x0	g(x)			0			x→ x0	g	′
									′(x)
lim	f (x)		=	0		=	lim	f	(x)	;	(3.19)
(x→∞ )							(x→∞ )

53

2) якщо lim

f (x) = ¥ та lim g(x) = ¥,

x→x0

x→x0

(x→∞ )

(x→∞ )

x→ x0

g(x)

x→ x0

g

¢(x)

lim

f

(x)

= ¥ = lim

f

¢(x)

.

(3.19*)

(x→∞ )

¥

(x→∞ )

За допомогою правила Лопіталя розкриваються невизначе-

0

¥

{0 × ¥}в границях (п.2.1.6).

ності типу

,

,

0

¥

Приклад

Знайти границі

1. lim

x

;

2.lim

x4

.

x→∞ ex

x→∞ a x

x

=

¥

= lim

(x)′

= lim

1

=

1

= 0

1. lim

;

x

(ex )¢

x

¥

x

→∞ e

¥

x →∞

x

→∞ e

x4

¥

(x4 )′

4 × x3

¥

2. lim

=

= lim

= lim

=

=

x

(a x )¢

x

ln(a)

x→∞ a

¥

x→∞

x→∞ a

¥

= lim

(4 × x3 )′

= lim

4 ×3× x2

=

¥

= lim

(12 × x2 )′

=

(a x ×ln(a))¢

x

ln

2

(a)

(a x ln2

(a))¢

x→∞

x→∞ a

¥

x→∞

= lim

12 × 2 × x

=

¥

= lim

(24 × x)′

= lim

24

=

24

= 0 .

x

ln

3

(a)

¥

(a x ln3 (a))¢

x

ln

4

(a)

¥

x→∞ a

x

→∞

x→∞ a

3.9 ЗАСТОСУВАННЯ ПОХІДНОЇ ДЛЯ ДОСЛІДЖЕННЯ ФУНКЦІЇ

Для дослідження характеру поведінки графіка функції

y= f (x) важливим є визначення:

–інтервалів монотонності функції (інтервалів зростання та спадання);

–характерних точок функції – точок локальних екстремумів функції і точок найбільшого або найменшого значення функції на інтервалі дослідження;

54

– інтервалів опуклості та угнутості функції та точок переги-

ну;

– характеру поведінки функції на безкінечності та за умов існування точок розриву (дослідження на наявність асимптот функції).

За умов наявності інформації про функцію за всіма цими пунктами графік функції можна легко побудувати на координатній площині. Всі указані пункти можуть бути визначені за допомогою похідних функції 1-го та 2-го порядку y′ = f ′(x) та y′′ = f ′′(x) .

3.9.1 ЗРОСТАННЯ, СПАДАННЯ ТА ЕКСТРЕМУМ ФУНКЦІЇ

Згадаємо, що функція y = f (x) називається строго монотонною на деякому інтервалі [a,b], якщо на цьому інтервалі для

неї виконуються умови "x1, x2 Î[a,b]: x2 > x1 f (x2 ) > f (x1 ) – умови зростання, або умови

"x1 , x2 Î[a,b]: x2 > x1 f (x2 ) < f (x1 ) – умови спадання.

Теорема про достатню умову зростання(спадання) функції

Якщо похідна диференційованої функції y = f (x) додатна (від’ємна) на деякому інтервалі [x1 , x2 ], то сама функція на цьому інтервалі монотонно зростає (спадає).

Доведення

Нехай функція y = f (x) диференційована і має додатну (від’ємну) похідну на інтервалі [x1 , x2 ], x1 < x2 .

Оскільки функція диференційована на інтервалі [x1 , x2 ], для неї виконується теорема Лагранжа

′
f (x2 )- f (x1 ) = f (x)(x2 - x1 ),		′	′	< 0).
де ξ Î[x1 , x2 ], оскільки ξ Î[x1 , x2 ] f (ξ) >			0 ( f (x)
′	′	(x)×(x2	- x1 ) < 0) і отже,
Тобто добуток f (ξ)× (x2 - x1 ) > 0	( f

f (x2 )- f (x1 ) > 0 ( f (x2 )- f (x1 ) < 0)

55

f (x2 ) > f (x1 ) ( f (x2 ) < f (x1 )).

Необхідна умова зростання (спадання) функції на інтер-

валі		y = f (x)
Якщо	функція			монотонно зростає (спадає) на
інтервалі	[x1 , x2 ],	то	її	похідна на	цьому інтервалі
набуває	не від’ємне		(не	додатне)	значення, тобто

′

′

£ 0).

"x Î[x1 , x2 ]: f (x) ³ 0

( f

(x)

y

tgα

3

y=f (x)

3

2

2

1

α

1

tga1

=

α1

α2

3

tga

=

2

0

a x1

x2

x3=b

0 x

tga3

=

f ′(x1 ) > 0
f ¢(x2 ) > 0 f (x) -
f ¢(x	) > 0
3

-1

Рисунок 3.6

Означення 1

Інтервали (проміжки), в яких функція зростає або спадає на-

зиваються інтервалами (проміжками) монотонності даної фу-

нкції.

Екстремум функції

Означення 2

Точка x0 називається точкою максимума функції y = f (x) , якщо у будь -якому достатньо малому околі δ цієї точки для всіх x δ виконується нерівність

f (x) £ f (x0 ).

56

Точка x0 називається точкою мінімума функції f (x) , як-

що у будь -якому достатньо малому околі δ цієї точки для всіх x δ виконується нерівність

f (x) ³ f (x0 ) .

Значення функції f (x) у цих точках називають відповідно максимумом і мінімумом функції f (x) . Позначають відповід-

но fmax (x) та fmin (x). Можна записати
fmax (x) = f (x0 ): ("x Î				x0 - x				< d,	d ® 0): ( f (x) < f (x0 )) ;	(3.20)
fmin (x) = f (x0 ): ("x Î		x0 - x				< δ ,			δ ® 0): ( f (x) > f (x0 )).	(3.20*)

Мінімум і максимум функції y = f (x) об’єднуються загаль-

ною назвою екстремум функції.

Виходячи з визначення екстремума, можна зробити висновок, що екстремум є найбільшим (найменшим) значенням функції в деякому малому околі точки x0 , тому екстремум функції

називають локальним екстремумом функції. На інтервалі до-

слідження функції, який значно відрізняється від 0, функція може мати декілька максимумів (мінімумів).

tgα

y

y=f (x)

						tga1	=
			α	α	α	tga2	=
			1
					3
	0		x1	2		tga3 =
		a		b	0 x

f ¢(a) < 0
f ¢(x ) < 0 f (x)¯
1
f ¢(b) < 0

Рисунок 3.7

57

В економіці поширена назва локального екстремума лока-

льний оптимум. А процес його знаходження – оптимізацією. Необхідна умова існування екстремума. Якщо диференці-

йована функція y = f (x) в точці x0 має локальний екстремум,

то для неї виконані умови теореми Ферма (досягає найбільшого (найменшого) значення у внутрішній точці деякого інтервалу). Отже, за цією теоремою, в екстремальній точці

f ′(x0 ) = 0 .

(3.21)

Але функція може досягати екстремума і в точках, в яких похідна не існує, або дорівнює безкінечності. Наприклад,

функція f (x) =

x

у точці

x = 0 похідної

немає (див. п. 3.5,

приклад 1), а екстремум у цій точці є –

fmin = 0 .

Функція y = 3

y′ =

2

. В точці x = 0 ,

x2 має

похідну

33

x

y′ = ∞ , але екстремум у цій точці є.

Отже, виходячи із вищесказаного, необхідні умови існу- вання екстремума можуть бути сформульовані таким чином.

Для того, щоб функція y = f (x)	мала екстремум у точці
x0 необхідно, щоб її похідна в	цій точці дорівнювала

0 ( f ′(x0 ) = 0), або не існувала.

Точки, в яких виконується необхідна умова існування екст-

ремума називаються критичними, або стаціонарними. Вони повинні належати області визначення функції D( f (x)).

Отже, якщо в якихось точках інтервалу дослідження функції є екстремум, то ці точки критичні (наведені умови виконуються).

Але не навпаки. Треба відзначити, що виконання необхідних умов не дає гарантії існування екстремума. Критична точка може не бути точкою екстремума.

58

Приклад 1

Знайти критичні точки і впевнитися в існуванні екстремумів

у цих точках для функцій y =

x2

− 4; y = x3 + 8 .

9

Розв’язання

1. Функція y =

x2

− 4 . Знайдемо критичні точки

9

y′ =

2x

= 0; x

= 0 .

k

9

Функція y′ =

2x

- це пряма лінія, яка набуває від’ ємного

9

значення для всіх точок x < 0

і додатне для всіх точок x > 0 .

Отже, після критичної точки функція y =

x2

− 4 змінює свій тип

9

із спадаючої на зростаючу. Очевидно, що в точці x = 0 вона має найменше значення, тобто ymin = y(0) = −4 .

2. Функція y = x3 + 8 . Знайдемо критичні точки

y′ = 3x2 = 0; x	k	= 0 .

Функція y′ = 3x2 на всій ОВФ набуває тільки додатні значення, отже, дана функція y = x3 + 8 завжди монотонно зростає і

у неї не може бути найбільшого чи найменшого значення на інтервалі (− ∞;+∞).

Висновок: Функція y = x3 + 8 у точці xk = 0 екстремума не

має.

Таким чином, щоб знайти дійсні точки екстремума, треба додатково проаналізувати критичні точки, тобто ввести ще достатні умови існування екстремума.

59

Достатні умови існування екстремума.

Перша достатня умова. Нехай функція y = f (x) диференційована і має критичну точку x0 . Якщо похідна y′ переходячи через критичну точку:

1) змінює свій знак з „+” на „-” , то в точці y = x0 знахо-

диться максимум функції y = f (x). ymax = y(x0 );

2) змінює свій знак з „-” на „+” , то в точці y = x0 знахо-

диться мінімум функції y = f (x). ymin = y(x0 );

3) не змінює свій знак, то в точці y = x0 екстремума немає.

Доведення

Якщо на якомусь проміжку похідна функції y = f (x) додат-

на, то цей проміжок, згідно з достатньою умовою монотонного зростання функції, – проміжок зростання цієї функції. Від’ємна похідна визначає проміжок спадання.

Отже, якщо процес зростання функції змінюється на спадання, то в точці зміни характеру процесу функція набуває максимального значення; якщо спадання змінюється на зростання, то

– мінімального, а коли процес не змінюється, похідна не змінює знак, то функція не має екстремального значення.

Звернемо увагу, що для доведення не використовувалася умова існування похідної в критичній точці.

Друга достатня умова існування екстремума функції в

точці.	y = f (x) двічі диференційована в деякій то-
Нехай функція
чці x0 . Якщо перша похідна цієї функції			′
			y (x0 ) = 0 , а друга –
′′	′′		що x0 – точка міні-
y (x0 ) ¹ 0 , то за умови y (x0 ) > 0 , маємо,
муму функції y =	f (x), а в разі, коли	′′		маємо, що x0 –
		y (x0 ) < 0 ,
точка максимуму функції y = f (x)		Якщо ж		′′
				y (x0 ) = 0 , то в

точці x0 екстремума немає.