
- •Міністерство освіти і науки україни
- •1. Подвійний інтеграл, його властивості. Обчислення подвійного інтеграла в декартових координатах
- •Властивості подвійного інтеграла
- •Обчислення подвійного інтеграла в декартових координатах
- •Зразки розв’язування задач
- •Рис 1.7
- •Завдання для самостійної роботи
- •2. Обчислення подвійного інтеграла в полярній системі координат. Застосування подвійних інтегралів до задач геометрії.
- •Зразки розв’язування задач
- •Завдання для самостійної роботи
- •3. Застосування подвійного інтеграла для деяких задач механіки
- •Момент інерції пластинки
- •Зразки розв’язування задач
- •Завдання для самостійної роботи
- •4. Обчислення криволінійних інтегралів першого та другого роду. Формула Гріна. Умови незалежності криволінійного інтеграла від шляху інтегрування
- •Властивості криволінійних інтегралів
- •Обчислення криволінійних інтегралів першого роду за плоскою областю
- •За плоскою областю
- •Зразки розв’язування задач
- •Завдання для самостійної роботи
- •5. Звичайні диференціальні рівняння. Диференціальне рівняння першого порядку.
- •Види диференціальних рівнянь першого порядку:
- •Зразки розв’язування задач
- •Завдання для самостійної роботи
- •6. Диференціальні рівняння вищих порядків. Диференціальні рівняння, що припускають зниження порядку
- •Зразки розв’язування задач
- •Завдання для самостійної роботи
- •7. Лінійні однорідні рівняння другого порядку зі сталими коефіцієнтами
- •Зразки розв’язування задач
- •Завдання для самостійної роботи
- •8. Лінійні неоднорідні диференціальні рівняння другого порядку зі сталими коефіцієнтами із спеціальною правою частиною
- •Зразки розв’язування задач
- •Завдання для самостійної роботи
- •9. Метод варіації довільних сталих.
- •Завдання для самостійного розв’язування
- •Література
- •Вища математика в прикладах та задачах Частина IV
- •49600, М. Дніпропетровськ – 5, пр. Гагаріна, 4
Завдання для самостійної роботи
І.
З’ясувати чи будуть функції
![]() розв’язком відповідного рівняння:
розв’язком відповідного рівняння:
а)
![]() ;
;
б)
![]() ;
;
в)
![]() .
.
ІІ. Знайти загальні інтеграли рівнянь:
1)
![]() ;
5)
;
5)![]() ;
;
2)
![]() ;
6)
;
6)![]() ;
;
3)
![]() ;
7)
;
7)![]() ;
;
4)
![]() ;
8)
;
8)![]() .
.
ІІІ. Знайти частинні розв’язки диференціальних рівнянь :
1)
![]() ;
;
2)
![]() ;
;
3)
![]() ;
;
4)
![]() ;
;
5)
![]() ;
;
6)
![]() ;
;
7)
![]() ;
;
8)
![]() ;
;
IV.
Записати рівняння кривої, яка проходить
через точку
![]() ,
кутовий коефіцієнт дотичної до якої
дорівнює
,
кутовий коефіцієнт дотичної до якої
дорівнює![]() .
.
1)
![]() ;
;
2)
![]() ;
;
3)
![]() .
.
6. Диференціальні рівняння вищих порядків. Диференціальні рівняння, що припускають зниження порядку
Диференціальним
рівнянням
![]() -го
порядку називається рівняння вигляду
-го
порядку називається рівняння вигляду![]() .
Розв’язком такого рівняння називається
будь-яка диференційованаn
разів функція
.
Розв’язком такого рівняння називається
будь-яка диференційованаn
разів функція
![]() ,
яка перетворює дане рівняння на
тотожність, тобто
,
яка перетворює дане рівняння на
тотожність, тобто
![]() .
.
Задача
Коші для цього рівняння полягає у тому,
щоб знайти розв’язок
рівняння,
який задовольняє умовам:
![]()
![]() при
при![]() ,
де
,
де![]() - числа, які називаються початковими
умовами.
- числа, які називаються початковими
умовами.
Функція
![]() називаєтьсязагальним
розв’язком
даного диференціального рівняння
називаєтьсязагальним
розв’язком
даного диференціального рівняння
![]() -го
порядку, якщо при відповідному виборі
довільних сталих
-го
порядку, якщо при відповідному виборі
довільних сталих![]() ця функція є розв’язком будь-якої задачі
Коші, що поставлена для цього рівняння.
Будь-який розв’язок,
який отриманий із загального розв’язку
при конкретних значеннях сталих
ця функція є розв’язком будь-якої задачі
Коші, що поставлена для цього рівняння.
Будь-який розв’язок,
який отриманий із загального розв’язку
при конкретних значеннях сталих
![]() ,
називаєтьсячастинним
розв’язком
цього
рівняння.
,
називаєтьсячастинним
розв’язком
цього
рівняння.
Рівняння вигляду
 .
.
Розв’язок
цього рівняння отримується
![]() -
кратним інтегруванням, тобто:
-
кратним інтегруванням, тобто:
![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() ,
де
,
де
![]() .
.
2)
Диференціальне
рівняння
![]() ,
що явно не містить шукану функцію
,
що явно не містить шукану функцію
![]() ,
за допомогою підстановки
,
за допомогою підстановки
![]() ;
;
![]() зводять
до відповідного рівняння першого порядку
зводять
до відповідного рівняння першого порядку
![]() .
Розв’язок
цього рівняння знаходять, виходячи з
його типу, а потім, для отримання
загального розв’язку
початкового рівняння,
.
Розв’язок
цього рівняння знаходять, виходячи з
його типу, а потім, для отримання
загального розв’язку
початкового рівняння,
![]() .
.
3)
Диференціальне
рівняння вигляду
![]() ,
що явно не містить незалежну зміну
,
що явно не містить незалежну зміну
![]() ,
підстановкою
,
підстановкою![]() зводять до диференціального рівняння
першого порядку
зводять до диференціального рівняння
першого порядку![]()
Зразки розв’язування задач
Приклад 1. Розв’язати рівняння:
![]() .
.
Розв’язання.
Права
частина рівняння не містить невідомої
функції
![]() та її похідної
та її похідної![]() ,
тому для отримання розв’язку тричі
послідовно інтегруємо обидві його
частини:
,
тому для отримання розв’язку тричі
послідовно інтегруємо обидві його
частини:
![]() ,
,
![]() ,
,
![]()
![]() .
.
Отже, загальний розв’язок даного рівняння:
![]() .
.
Приклад 2. Знайти загальний розв’язок рівняння:
![]() .
.
Розв’язання.
Дане рівняння того же типу, що і попереднє, тому його розв’язок знаходимо аналогічно, тобто:
![]() .
.
За методом інтегрування частинами, маємо
 ,
,
![]() ,
,
![]() ,
,
![]()
 =
=![]() .
.
Тоді загальний розв’язок рівняння має вигляд:
![]() ,
,
або
![]() .
.
Приклад 3. Розв’язати задачу Коші:
![]() .
.
Розв’язання.
![]() ,
,
![]() .
.
Отже, загальний розв’язок рівняння:
![]() .
.
Для
того, щоб отримати частинний розв’язок,
тобто, розв’язати задачу Коші, треба
знайти
![]() та
та![]() ,використовуючи початкові умови:
,використовуючи початкові умови:
![]() ,
,
![]() .
.
Таким
чином,
![]() частинний розв’язок рівняння.
частинний розв’язок рівняння.
Приклад 4. Знайти частинний розв’язок рівняння:
![]() .
.
Розв’язання.
Знайдемо загальний розв’язок інтегруванням:
![]()
![]()

![]() .
.
![]()

![]() .
.
Знайдемо
![]() та
та![]() .
Підставимо початкові умови у вирази з
.
Підставимо початкові умови у вирази з![]() та
та![]() .
.
![]() ;
;
![]() .
.
Тоді, частинний розв’язок рівняння має вигляд:
![]() .
.
Приклад 5. Розв’язати рівняння:
![]() .
.
Розв’язання.
Дане
рівняння не містить явно функції
![]() ,
тому зводимо його до рівняння першого
порядку підстановкою
,
тому зводимо його до рівняння першого
порядку підстановкою![]() ,
тоді
,
тоді![]() .
Маємо:
.
Маємо:
![]() ,
,
![]()
![]() .
.
Отже,
![]() .
Інтегруючи це рівняння, дістанемо
.
Інтегруючи це рівняння, дістанемо
![]() .
.
Приклад 6. Розв’язати рівняння:
![]() .
.
Розв’язання.
Аналогічно
попередньому прикладу введемо підстановку
![]()
![]() .
Отримаємо рівняння першого порядку:
.
Отримаємо рівняння першого порядку:
![]() ,
,
яке
є лінійним рівнянням. Його розв’язок
будемо шукати у вигляді
![]() ,
а
,
а![]() :
:
![]() ,
,![]() ,
,

І.
![]()
![]()
![]() .
.
ІІ.

![]() .
.
Маємо
![]() ,
або
,
або![]() .
.
Тоді
![]() .
Проінтегруємо це рівняння:
.
Проінтегруємо це рівняння:
![]() .
.
Із
попереднього
![]() .
.
Маємо
![]() ,
або
,
або
![]() загальний розв’язок.
загальний розв’язок.
Приклад 7. Розв’язати рівняння:
![]() .
.
Розв’язання.
Рівняння
явно не залежить від функції
![]() ,
тому підстановкою
,
тому підстановкою![]() зводимо його до диференціального
рівняння першого порядку:
зводимо його до диференціального
рівняння першого порядку:
![]() ,
,
яке
є однорідним. Використовуємо заміну
![]() та отримаємо рівняння з відокремлюваними
змінними:
та отримаємо рівняння з відокремлюваними
змінними:
![]() ,
або
,
або
![]() .
.
До
інтеграла, що стоїть у лівій частині
останнього рівняння застосуємо заміну
![]() .
Дістанемо:
.
Дістанемо:
![]()
![]() .
.
Маємо диференціальне рівняння першого порядку, яке розв’язуємо простим інтегруванням:
![]() .
.

![]() .
.
Отже, загальним розв’язком даного рівняння буде функція:
![]() .
.
Приклад 8. Розв’язати задачу Коші:
![]() .
.
Розв’язання.
Аналогічно
попередньому, маємо:
![]() .
Тоді
.
Тоді
![]() .
.
Це рівняння з відокремлюваними змінними. Відокремлюємо змінні та обчислюємо отримані інтеграли:
![]()
![]()
![]() ;
;
![]() загальний
розв’язок.
загальний
розв’язок.
Використаємо початкові умови:
![]()
Отже, розв’язок задачі Коші має вигляд:
![]() .
.
Приклад 9. Розв’язати задачу Коші:
![]() .
.
Розв’язання.
Це
рівняння явно не містить незалежну
змінну
![]() ,
тому слід використати підстановку
,
тому слід використати підстановку![]() яка зведе наше рівняння до рівняння
першого порядку:
яка зведе наше рівняння до рівняння
першого порядку:
![]() .
.
Відокремимо змінні, та обчислимо одержані інтеграли:
![]()

![]() .
.
Останнє рівняння – це диференціальне рівняння першого порядку з відокремлюваними змінними. Розв’яжемо його:
![]() .
.
Отже, загальний інтеграл даного рівняння другого порядку:
![]() .
.
Приклад 10. Розв’язати рівняння:
![]() .
.
Розв’язання.
Аналогічно
попередньому прикладу вводимо підстановку
![]() ;
;![]() .
Дістанемо:
.
Дістанемо:
![]()
![]()
![]() .
.
Для інтеграла, що знаходиться у лівій частині останнього рівняння, зробимо підстановку:
![]()
![]()
![]() .
.
Отже:
![]() .
.
Обчислимо
інтеграл
![]() .
Підінтегральна функція представляє
собою правильний раціональний дріб,
який можна розкласти на простіші:
.
Підінтегральна функція представляє
собою правильний раціональний дріб,
який можна розкласти на простіші:
![]()
![]()
![]() ;
;
Тоді:
![]() .
.
Для
знаходження невідомих чисел
![]() по черзі прирівнюємо
по черзі прирівнюємо![]() кожному із коренів знаменника, а потім,
оскільки, невідомих більше ніж різних
коренів знаменника, прирівнюємо
коефіцієнти при
кожному із коренів знаменника, а потім,
оскільки, невідомих більше ніж різних
коренів знаменника, прирівнюємо
коефіцієнти при![]() в однакових ступенях в останній рівності.
Дістанемо:
в однакових ступенях в останній рівності.
Дістанемо:

Отже,
![]()
![]()
![]() =
=
![]() ;
;
Повертаючись до старої змінної, маємо:
 ,
або
,
або
![]() загальний
інтеграл рівняння.
загальний
інтеграл рівняння.
Приклад 11. Знайти частинний розв’язок рівняння:
![]() .
.
Розв’язання.
Підстановкою
![]() початкове рівняння зводиться до рівняння
Бернуллі першого порядку:
початкове рівняння зводиться до рівняння
Бернуллі першого порядку:
![]() ,
або
,
або![]() .
.
Розв’язок
цього рівняння шукаємо у вигляді
![]() .
Тоді
.
Тоді![]() .
.
![]() ,
,
![]()
![]() ,
,


І.
![]() .
.
II.

![]() .
.
Дістанемо:
![]() .
.
Отже
![]()
 .
.
Загальний інтеграл рівняння матиме вигляд:
![]() .
.
Використовуючи
початкові умови, знайдемо
![]() та
та![]() :
:
![]()


Таким чином, частинний розв’язок рівняння має вигляд:
![]() .
.
Приклад 12. Знайти частинний розв’язок рівняння:
![]() .
.
Розв’язання.
Підстановкою
![]() зведемо дане рівняння до однорідного
рівняння І-го порядку
зведемо дане рівняння до однорідного
рівняння І-го порядку![]() ,
яке за допомогою заміни
,
яке за допомогою заміни![]() перетвориться на диференціальне рівняння
з відокремлюваними змінними:
перетвориться на диференціальне рівняння
з відокремлюваними змінними:
![]() ,
або
,
або
![]()
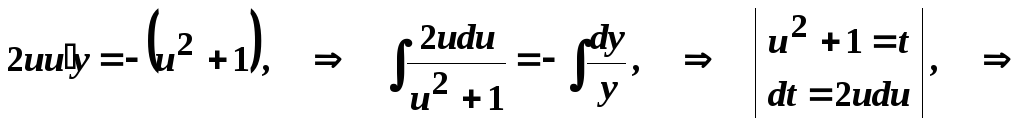
![]()
![]()
![]()
![]() ,
або
,
або
![]() .
.
Тобто,
![]() ,
або
,
або .
.
Оскільки
![]()
![]() .
.
Дістанемо:
 ,
або
,
або
![]() загальний інтеграл рівняння.
загальний інтеграл рівняння.
З початкових умов випливає:



Отже, частинний розв’язок рівняння має вигляд:
![]() .
.
