Зразки розв’язування задач

Приклад 1. Обчислити інтеграл , якщо областьпоширена на інтервалі.

Розв’язання.

Шуканий інтеграл дорівнює

.

Для функції , яка розглядається як функція відпри постійному, первісною буде функція.

Тому

.

Шуканий подвійний інтеграл дорівнює:

.

Приклад 2. Змінити порядок інтегрування у повторному інтегралі

Розв’язання.

Побудуємо область інтегрування D, визначивши криві та прямі, якими обмежена ця область (рис. 1.4).

Рис. 1.4

Область аналітично має вигляд:Межі інтегрування вибираємо по змінній, для цього спроектуємо область на вісь. Областьпроектується на відрізокосі. Абсциса у цих межах змінюється віддо. Таким чином, змінивши порядок інтегрування, матимемо:

.

Приклад 3. Обчислити подвійний інтеграл , якщо областьобмежена кривими: ;;.

Розв’язання. Область інтегрування зображена на рис. 1.5.

Рис.1.5

Для обчислення заданого інтеграла краще скористатися формулою (1.3):

Приклад 4. Розставити границі інтегрування двома способами й обчислити подвійний інтеграл

,

якщо область інтегрування обмежена лініями: .

Розв’язання.

Область інтегрування зображена на рис. 1.6.

Рис. 1.6

Для обчислення заданого інтеграла скористаємось спочатку формулою (1.3.):

.

Останній інтеграл проінтегруємо за частинами: ;;;.Тоді

;

.

Якщо для обчислення даного інтеграла скористатися формулою (1.4), то

і при;

і при.

Отже, область D треба розбити на дві області, після чого маємо:

тобто ми одержали такий же результат, що й раніше.

Приклад 5. Змінити порядок інтегрування й обчислити повний інтеграл

.

Розв’язання.

Побудуємо область інтегрування D, яка обмежена кривою , прямоюта віссю(рис.1.7.).

Рис 1.7

Спроектуємо область D на вісь у відрізок, на якомузмінюється віддо.

Таким чином ,

Завдання для самостійної роботи

Ι. Змінити порядок інтегрування у повторному інтегралі:

а) ;

б) ;

в) ;

г) .

ΙΙ. Обчислити подвійний інтеграл:

а) ,

б)

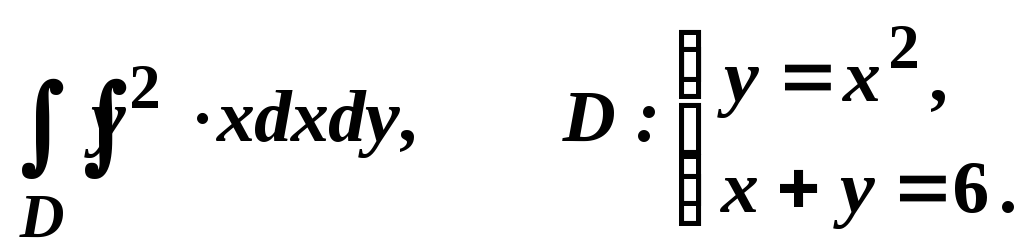
в)

г)

2. Обчислення подвійного інтеграла в полярній системі координат. Застосування подвійних інтегралів до задач геометрії.

У випадку полярної системи координат . Тоді елемент площі в полярних координатах має вигляд:

.

Подвійний інтеграл в полярній системі координат обчислюється за формулою:

(2.1)

деівідповідно найменше й найбільше значення змінноїв областіірівняння межі(рис. 2.1).

Рис. 2.1

Об’єм тіла. Для циліндричного тіла твірні якого паралельні осі , яке обмежене знизу областюплощини, а зверху – поверхнею, об’єм обчислюється за наступною формулою:

(2.2)

де функція неперервна в області.

Площа поверхні обертання. Якщо поверхня проектується на площинуу вигляді області, то площа поверхніобчислюється за формулою:

. (2.3)

Площа плоскої фігури. Якщо , а, то циліндричне тіло, об’єм якого обчислюється за формулою (2.2), перетворюється в прямий циліндр з висотою, яка дорівнює 1. Об’єм такого циліндра дорівнює площі його основи. Отже, площа областібуде обчислюватися за формулою:

. (2.4)

Для полярної системи координат .