5. Вторичные (характеристические) параметры четырехполюсников согласованный режим четырехполюсника.

Для несимметричных четырехполюсников можно подобрать такую пару сопротивлений и, для которых соблюдаются следующие условия:

1. Входное со­противление со стороны выводов 1–1 , если к выводам 2–2 подключено сопротивление (рис. 3.7, а).

2. Входное сопротивление со стороны выводов 2–2 , если к выводам 1–1 подключено сопротивление (рис. 3.7, б).

и называютхарактеристическими сопротивлениями (характеристическими параметрами) четырехполюсника.

Выразим ичерезА–параметры:

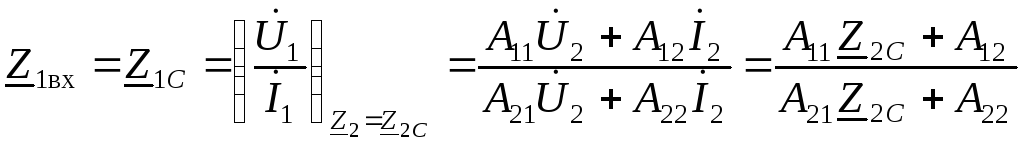. (3.23)

При выводе этого соотношения числитель и знаменатель дроби разделили на и учли, что при.

Из уравнений (3.11) следует, что

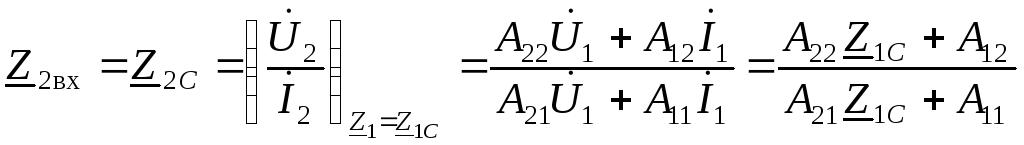. (3.24)

При выводе соотношения (3.24) числитель и знаменатель дроби разделили на и учли, что при принятых условиях.

Решая совместно уравнения (3.23) и (3.24) относительно и(два уравнения с двумя неизвестными), получим:

(3.25)

. (3.26)

Учитывая (3.12) – (3.15), получим

. (3.27)

Третьим характеристическим параметром четырехполюсника является постоянная передачи (или мера передачи), которая характеризует четырехполюсник как элемент, через который передается мощность, и в общем случае представляет собой комплексное число

, (3.28)

где –постоянная ослабления, –постоянная фазы.

Физический смысл величин ипоясним ниже.

Постоянная передачи должна удовлетворять условиям

, (3.29)

. (3.30)

Эти выражения не противоречат соотношению (3.10), т.к.

.

, ,называютвторичными параметрами четырехполюсника. Эти величины независимы друг от друга и являются функциями параметров четырехполюсника.

Режим работы четырехполюсника на нагрузку, равную его характеристическому сопротивлению, называется согласованным режимом работы.

6. Несинусоидальные токи. Разложение в ряд Фурье. Частотный спектр несинусоидальной функции напряжения или тока.

Обычно анализ цепей переменного тока проводится в предположении, что действующие в них ЭДС и токи имеют синусоидальную форму. В большинстве случаев такое предположение оправдано, однако, на самом деле форма токов и напряжений в той или иной степени всегда несинусоидальна.

Искажение ЭДС и токов может возникать вследствие конструктивных особенностей генераторов переменного тока, приводящих к тому, что создаваемая ими ЭДС несинусоидальна, либо вследствие нелинейности элементов электрической цепи. Причем для появления искажений достаточно наличия в цепи только одного нелинейного элемента. Чаще всего обе эти причины присутствуют одновременно, но в зависимости от степени выраженности их воздействия на цепь пренебрегают одной из них или обеими сразу.

Из курса математики известно, что любую несинусоидальную периодическую функцию  удовлетворяющую условиям Дирихле, т.е. имеющую за полный период конечное число максимумов, минимумов и разрывов первого рода, можно представить в виде ряда Фурье

F(t) = A₀ + A₁sin(t+ ₁) + A₂sin(2t+ ₂) + + A_ksin(kt+ _k)+ = A₀ + B₁sint + B₂sin2t + + B_ksinkt+ ј + C₁cost + C₂cos2t + + C_kcoskt +A₀+a₁+a₂+ + a_k+ ,

г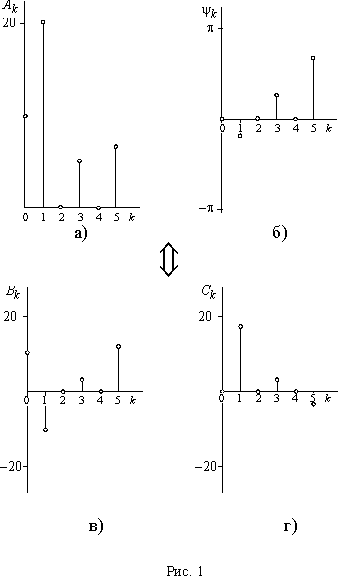де.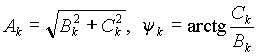

Первый член ряда A₀ называется постоянной составляющей или нулевой гармоникой. Второй член A₁sin(t+ ₁) имеет частоту равную частоте функции F(t) и называется первой или основной гармонической составляющей (коротко - гармоникой). Остальные члены ряда вида A_ksin(kt+ _k) имеют частоты в целое число раз k больше частоты основной гармоники и называются высшими гармоническим составляющими или гармониками. Каждая высшая гармоника в отдельности именуется по номеру k , т.е. вторая гармоника, третья гармоника и т.д.

Из выражения (1) следует, что каждую гармонику ряда Фурье можно представить в виде двух составляющих - синусной B_ksinkt и косинусной C_kcoskt. Амплитуды этих составляющих B_k и C_k называются коэффициентами ряда Фурье.

Разложение в ряд Фурье всегда однозначно в отношении постоянной составляющей, а также амплитуд и частот гармонических составляющих. В то же время, начальные фазы гармоник изменяются при изменении момента времени, принятого за начало отсчета. Таким образом, ряд Фурье можно определить, задав номера, амплитуды и начальные фазы гармоник или номера и амплитуды синусной и косинусной составляющих гармоник. Совокупность амплитуд A_k и начальных фаз _ называются соответственно амплитудным и фазовым частотными спектрами, а совокупность коэффициентов B_k и C_k - частотным спектром функции. Спектры функций удобно изображать отрезками прямых линий, пропорциональных соответствующим величинам (рис). На показаны два варианта частотных спектров ряда Фурье u(t)=10+20sin(500t /6)+5sin(1500t+ /4)+7sin(2500t+2 /3).

Пусть t =  . Тогда разложение в ряд функции F( ), имеющей период 2 , будет

F( ) = A₀ + B₁sin + B₂sin2 + + B_ksink +

ј + C₁cos + C₂cos2 + + C_kcosk + =

= A₀ + A₁sin( +₁) + A₂sin(2 +₂) + + A_ksin(k +_k)+ .

Для этой функции коэффициенты ряда Фурье можно найти из выражений