
- •1. Основные уравнения четырехполюсников. Определение коэффициентов.
- •2. Уравнения нагруженного четырехполюсника в а-форме. Входные сопротивления. Коэффициент передачи по напряжению и току. Расчет коэффициентов.
- •3. Схемы соединения четырехполюсников. Обратные связи.
- •Каскадное соединение
- •Последовательное соединение
- •4. Схемы замещения четырехполюсников.
- •5. Вторичные (характеристические) параметры четырехполюсников согласованный режим четырехполюсника.
- •6. Несинусоидальные токи. Разложение в ряд Фурье. Частотный спектр несинусоидальной функции напряжения или тока.
- •7. Максимальное, среднее и действующее значения несинусоидального тока.
- •8. Резонанс в цепи несинусоидального тока.
- •9. Мощность цепи несинусоидального тока.
- •10. Высшие гармоники в трехфазных цепях. Простейший утроитель частоты.
- •11. Возникновение переходных процессов в линейных цепях. Законы коммутации.
- •12. Классический метод расчета переходных процессов. Формирование расчетного уравнения, степень расчетного уравнения. Граничные условия.
- •Классический метод расчёта переходных процессов
- •13. Свободный и принужденный режимы. Постоянная времени цепи, определение длительности переходного процесса.
- •14. Периодический заряд конденсатора. Собственная частота колебаний контура. Критическое сопротивление.
- •15. "Некорректные" начальные условия. Особенности расчета. Существуют ли в реальных схемах такие условия?
- •16. 0Пределение корней характеристического уравнения. Обосновать.
- •17.Включение пассивного двухполюсника под действие кусочно-непрерывного напряжения. Формула Дюамеля.
- •Последовательность расчета с использованием интеграла Дюамеля
- •18. Реакция линейных цепей на единичные функции. Переходная и импульсная характеристики цепи, их связь.
- •Переходная и импульсная характеристики
- •19. Применение преобразований Лапласа к расчету переходных процессов. Основные свойства Лапласовых функций.
- •20.Операторные схемы замещения. Обосновать.
- •21.Расчет переходных процессов методом переменных состояния. Формирование расчетных уравнений. Расчет с помощью эвм.
- •22.Преобразование Фурье и его основные свойства. Частотные спектры импульсных сигналов, отличия от частотных спектров периодических несинусоидальных сигналов.
- •23.Расчет частотных характеристик цепи. Определение переходной характеристики по вещественной частотной.
- •24. Особенности применения частотного метода расчета при изучении прохождения сигнала через четырехполюсник.
- •25.Уравнения длинной линии в частных производных. Первичные параметры длинной линии.
- •26. Решение уравнений длинной линии при синусоидальном напряжении. Вторичные параметры длинной линии.
- •27. Волновые процессы в длинной линии. Падающая и отраженная волны. Коэффициент отражения. Входное сопротивление.
- •Дифференциальные уравнения длинной линии
- •Погонные параметры
- •Коэффициенты бегущей и стоячей волны
- •28.Линия без потерь. Стоячие волны.
- •29. Входные сопротивления линии без потерь. Имитация индуктивностей и емкостей.
- •30. Четвертьволновый трансформатор. Согласование линии с нагрузкой. Рассмотрите пример активно-реактивной нагрузки.
- •31. Волновые процессы в линии без потерь, нагруженной на активное сопротивление. Коэффициенты стоячей и бегущей волны.
- •32. Особенности вольт-амперных характеристик нелинейных элементов. Линейные схемы замещения по статическим и дифференциальным параметрам.
- •33. Расчет схем стабилизации напряжений и токов, определение коэффициента стабилизации по линейной схеме замещения.
- •34. Аппроксимация нелинейных характеристик. Аналитический метод расчета.
- •35. Особенности периодических процессов в электрических цепях с инерционными элементами.
- •36. Спектральный состав тока в цепи с нелинейным резистором при воздействии синусоидального напряжения. Комбинационные колебания.
- •37. Метод эквивалентных синусоид. Методы расчета нелинейных цепей по действующим значениям. Метод эквивалентной синусоиды.
- •Метод расчета нелинейных цепей переменного тока по эквивалентным действующим значениям
- •38. Форма кривых тока, магнитного потока и напряжения в нелинейной идеальной катушке. Схема замещения, векторная диаграмма.
- •Расчет тока катушки со сталью с учетом потерь в сердечнике
- •40. Феррорезонанс напряжений. Триггерный эффект.
- •41. Феррорезонанс токов. Скачкообразное изменение напряжения при питании от источника тока.
- •42. Основы метода гармонического баланса. Приведите пример.
- •43. Метод кусочно-линейной аппроксимации характеристик нелинейных элементов. Расчет цепей с вентилями. Схема однополупериодного и двухполупериодного выпрямителя.
- •Цепи с вентильными сопротивлениями
- •44. Расчет схемы однополупериодного выпрямителя с емкостью.
16. 0Пределение корней характеристического уравнения. Обосновать.
Пусть в цепи, конденсатор был заряжен до напряжения uC(0-) = U0. Исследуем процессы в контуре, образованном резистором, конденсатором и катушкой после замыкания в момент t = 0 ключа. Так как источники в цепи отсутствуют, то установившиеся составляющие решений равны нулю. Решение будет состоять из одной свободной составляющей.
По второму закону Кирхгофа t ≥ 0 имеем:
![]() .
.
Учитывая, что
![]() ,
получаем дифференциальное уравнение
второго порядка для свободной составляющей
напряжения
,
получаем дифференциальное уравнение
второго порядка для свободной составляющей
напряжения
 .
.
Характеристическое уравнение при этом имеет вид:
![]() .
.
Характер электромагнитных процессов в контуре зависит от соотношения параметров R, L, С, входящих в выражение для корней характеристического уравнения
 .
.
В зависимости от знака подкоренного выражения корни могут быть вещественными или комплексно-сопряженными. Они определяют характер свободных составляющих переходных токов и напряжений.
17.Включение пассивного двухполюсника под действие кусочно-непрерывного напряжения. Формула Дюамеля.
Зная реакцию цепи
на единичное возмущающее воздействие,
т.е. функцию переходной проводимости
![]() или
(и) переходную функцию по напряжению
или
(и) переходную функцию по напряжению![]() ,
можно найти реакцию цепи на воздействие
произвольной формы. В основе метода –
метода расчета с помощью интеграла
Дюамеля – лежит принцип наложения.
,
можно найти реакцию цепи на воздействие
произвольной формы. В основе метода –
метода расчета с помощью интеграла
Дюамеля – лежит принцип наложения.
При использовании
интеграла Дюамеля для разделения
переменной, по которой производится
интегрирование, и переменной, определяющей
момент времени, в который определяется
ток в цепи, первую принято обозначать
как
![]() ,
а вторую - как t.
,
а вторую - как t.

Пусть в момент
времени
![]() к
цепи с нулевыми начальными условиями
(пассивному двухполюсникуПД
на рис. 1)
подключается источник с напряжением
к
цепи с нулевыми начальными условиями
(пассивному двухполюсникуПД
на рис. 1)
подключается источник с напряжением
![]() произвольной
формы. Для нахождения тока
произвольной
формы. Для нахождения тока![]() в
цепи заменим исходную кривую ступенчатой
(см. рис. 2), после чего с учетом, что цепь
линейна, просуммируем токи от начального
скачка напряжения
в
цепи заменим исходную кривую ступенчатой
(см. рис. 2), после чего с учетом, что цепь
линейна, просуммируем токи от начального
скачка напряжения![]() и
всех ступенек напряжения до момента t,
вступающих в действие с запаздыванием
по времени.
и
всех ступенек напряжения до момента t,
вступающих в действие с запаздыванием
по времени.
В момент времени
t составляющая общего тока, определяемая
начальным скачком напряжения
![]() ,
равна
,
равна![]() .
.
В момент времени
![]() имеет
место скачок напряжения
имеет
место скачок напряжения![]() ,
который с учетом временного интервала
от начала скачка до интересующего
момента времени t обусловит составляющую
тока
,
который с учетом временного интервала
от начала скачка до интересующего
момента времени t обусловит составляющую
тока![]() .
.
Полный ток
![]() в
момент времени t равен, очевидно, сумме
всех составляющих тока от отдельных
скачков напряжения с учетом
в
момент времени t равен, очевидно, сумме
всех составляющих тока от отдельных
скачков напряжения с учетом![]() ,
т.е.
,
т.е.
![]()
 .
.
Заменяя конечный
интервал приращения времени
![]() на
бесконечно малый, т.е. переходя от суммы
к интегралу, запишем
на
бесконечно малый, т.е. переходя от суммы
к интегралу, запишем Соотношение
называетсяинтегралом
Дюамеля.
Соотношение
называетсяинтегралом
Дюамеля.
Следует отметить,
что с использованием интеграла Дюамеля
можно определять также напряжение. При
этом в (1) вместо переходной проводимости
![]() будет
входить переходная функция по напряжению.
будет
входить переходная функция по напряжению.
Последовательность расчета с использованием интеграла Дюамеля
Определение функции
 (или
(или )
для исследуемой цепи.
)
для исследуемой цепи.Запись выражения
 (или
(или )
путем формальной замены t на
)
путем формальной замены t на .
.Определение производной
 .
.Подстановка найденных функций в (1) и интегрирование определенного интеграла.
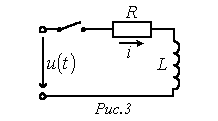
В качестве примера использования интеграла
Дюамеля определим ток в цепи рис. 3,
рассчитанный в предыдущей лекции с
использованием формулы включения.
качестве примера использования интеграла
Дюамеля определим ток в цепи рис. 3,
рассчитанный в предыдущей лекции с
использованием формулы включения.
Исходные данные
для расчета:
![]() ,
,![]() ,
,![]() .
.
Переходная проводимость

Полученный результат аналогичен выражению тока, определенному в предыдущей лекции на основе формулы включения.


