Построение модели Построение математической модели

Итак, далее будет рассмотрена непрерывно-стахостическая модель применительно к системе массового обслуживания. Основная задача теории массового обслуживания состоит в определении различных функциональных характеристик системы обслуживания, с тем чтобы найти ее слабые звенья. В дальнейшем, после получения результатов экспериментов, проводится работа по ликвидации этих слабых участков системы. При этом само по себе качество обслуживания в теории система массового обслуживания не принимается во внимание.

Имеется четырехканальная система массового обслуживания с отказами, на вход которой подается поток требований с интенсивностью и временем обслуживания каждой заявки . Если заявка поступает в систему, когда все каналы заняты, то она получает отказ и покидает систему необслуженной. Состояние системы будем отличать по числу занятых каналов. Рассмотрим следующие возможные состояния системы:

S₀— все каналы свободны,

S₁— занят ровно 1 канал, остальные 3 свободны,

S₂— занято ровно 2 канала, остальные 2 свободны,

S₃— занято ровно 3 канала, 1 свободен,

S₄— заняты все 4 канала.

Граф состояния системы.

   

S₀  S₁ 2 S₂ 3 S₃ 4 S₄

Таким образом получается, что плотность вероятности перехода системы из состояния S_i в состояниеS_i+1 определяется интенсивностью входного потока требований, а плотность вероятности перехода из состоянияS_i в состояниеS_i-1определяется суммарной интенсивностью обслуживанияiканалами, так как если в обслуживании занятоi каналов, то интенсивность этого обслуживания будет вiраз выше. Процесс протекающий в рассматриваемой системе массового обслуживания , представляет собой частный случай процесса гибели и размножения.

Введем обозначение P_k— вероятность того, что в момент времениtсистема находится в состоянииS_k.

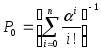, где,а.

Определим основные характеристики системы:

Р_отк— вероятность отказа, то есть вероятность занятости всех каналов системы:Р_отк=;

q— относительная пропускная способность, то есть вероятность того, что заявка будет принята к обслуживанию:q=1 — Р_отк =1 —P_n;

Mv — среднее число занятых каналов, равное среднему числу заявок находящихся в системе:Mv =.

Как видно из вышесказанного, эти характеристики нельзя принимать к данной модели, так как по условию задания нужно рассчитать в процессе моделирования, такие параметры системы, которые не выражаются в виде математических формул и уравнений. Поэтому необходимо построить имитационную модель, например, на каком-либо из языков программирования.

Описание случайностей для построения имитационной модели.

Для построения имитационной модели необходимо более тщательно рассмотреть входящий поток требований и время обслуживания одной заявки, так как эти характеристики стахостичны.

Практически наиболее часто входящий поток требований предполагается пуасоновским ( простейшим ), то есть потоком обладающим свойствами стационарности, ординарности и отсутствием последствий. Следовательно имеющийся в моделируемой системе массового обслуживания поток входящих требований — пуасоновский. В этом случае вероятность P(X(T)=k)того, что число требованийX(T), поступающих на обслуживание в промежуток времени продолжительностьюt, равноk,определяется по формуле

(1)

где — интенсивность потока, то есть среднее число его требований, поступающих в систему в единицу времени. Далее представляется график соответствующий распределению Пуасона дляk=1 и=, то есть для интенсивности имеющейся системы.

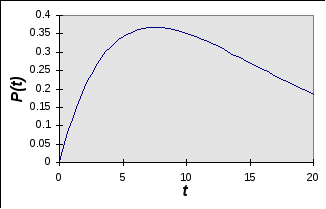
Как видно из этого графика максимальная вероятность достигается при tравном 7.5, то есть при, что соответствует условию задачи, так как величина обратнаяимеет физический смысл времени прихода одной заявки.

Формула (1) дает распределение вероятности числа требований, поступающих на обслуживание за данный промежуток времени t. Вместо этого можно пользоваться распределением вероятностей промежутка времениТмежду двумя последовательными моментами поступления заявок. Это распределение получается автоматически из формулы (1) приk=0.

(2)

Отсюда для соответствующей плотности вероятностей имеем

(3)

то есть длительность интервала времени между двумя последовательными моментами поступлениями требований пуасоновского потока имеет показательное (оно же экспоненциальное) распределение.

Теперь рассмотрим основную характеристику функционирования прибора — время обслуживания требования этим прибором. Этот показатель характеризует не качество обслуживания, а лишь пропускную способность прибора. Время обслуживания непостоянно. Оно зависит от многих неконтролируемых факторов. Например, продолжительность проведения профилактического ремонта автомобиля зависит от его марки, модели, степени износа и пр.. Поэтому время обслуживания требования прибором в общем случае является случайной величиной, при этом считают, что продолжительности обслуживания разных требований прибором — независимые случайные величины с одним и тем же законом распределения. Наиболее часто полагают этот закон распределения экспоненциальным.

В случае экспоненциального закона распределения времени обслуживания плотность вероятности имеет вид:

, (4)

где параметр имеет простой физический смысл: обратная его величина —равна среднему времени обслуживания требования прибором.

Функция распределения имеет вид:

(5)

Из формулы (3) (плотность распределения длительности интервала времени между двумя последовательными моментами поступлениями требований пуасоновского потока) и формулы (4) (плотность распределения длительности времени обслуживания одной заявки) видно, что обе случайные величины имеют показательное (оно же экспоненциальное) распределение, в общем виде имеющее следующий вид: (6)

и функцию распределения: . (7)

При экспоненциальном распределении времени обслуживания и времени поступления требований существенно упрощаются все теоретические выкладки, при этом окончательные результаты оказываются справедливыми и для произвольного закона распределения с тем же математическим ожиданием.

Из всего выше сказанного следует, что экспоненциальный закон распределения подходит для моделирования случайностей и во времени обслуживания и во времени поступления требований.

Пусть мы располагаем датчиком псевдослучайных чисел, равномерно распределенных на отрезке (0,1) — R(0,1). Тогда если случайная величинаХимеет плотность распределения вероятностейf(x),то распределение случайной величиныR, такой, что, является равномерным на отрезке (0,1). Это означает, что если существует элементарное преобразование для получения обратной функцииF^-1(x)для нашей случайной величиныХ, то для ее реализации нужно воспользоваться формулойX= F^-1(R).

Для формулы (7) (общий случай) имеем . Если случайная величинаR распределена равномерно на интервале (0,1) , то и величина 1 —Rраспределена так же равномерно и на том же интервале (0,1). Поэтому имеем, а для конкретных случаев:

для времени поступления требований;

для времени обслуживания.