2.4. Вычисление обратных матриц

1. По методу Гаусса. Всякая неособенная матрица, для которой, имеет обратную матрицу. Очевидно, чтоА*А^–1 =Е. запишем это равенство в виде системыnуравнений сnнеизвестными

; (37)

где а_ik – элементы матрицыА;

z_kj– элементы обратной матрицы (А^–1);

_ij– элементы единичной матрицы.

При этом _ij =

Для нахождения элементов одного столбца обратной матрицы необходимо решить соответствующую линейную систему (37) с матрицей А. Так для полученияj-го столбца дляА^–1(z_1j, z_2j,…z_nj) решается система:

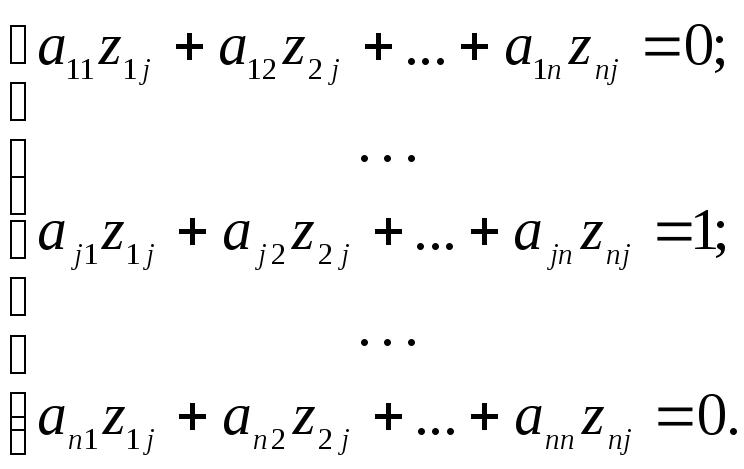(38)

Следовательно для обращения матрицы Анужноnраз решить систему (38) приj=. Поскольку матрицаАсистемы не меняется, то исключение неизвестных осуществляется только один раз, а (n–1) раз при решении (38) делается только обратный ход с соответствующим изменением правой ее части.

2. Другой подход к определению обратной матрицы а–1

,

где – определитель матрицы,А_ij – алгебраические дополнения соответствующих элементов матрицыА.

3. Обращение матрицы а посредством треугольных матриц

Известно, что всякая обратная матрица, если она существует, то по структуре будет такая же, как и исходная, т.к.

А^–1А =АА^–1=Е=. (39)

Рассмотрим пример обращения матрицы 3-го порядка следующего вида:

А=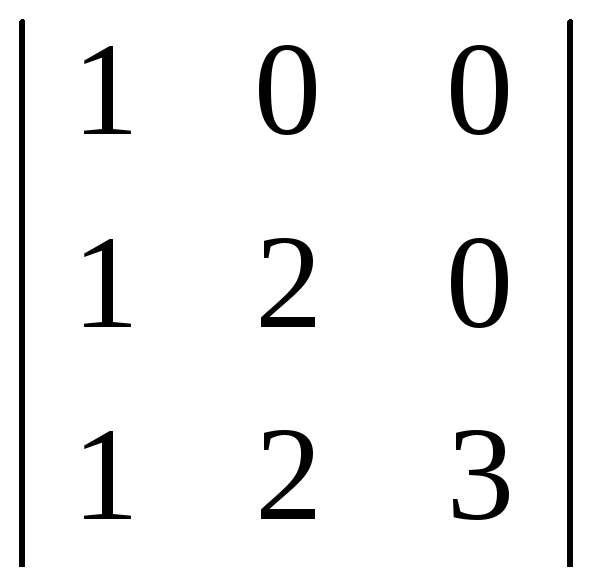. (40)

Решение. МатрицуА^–1 ищем в виде

А^–1=. (41)

Перемножая АиА^–1 с учетом (39) будем иметьt₁₁ = 1;t₁₁ + 2t₂₁ = 0; 2t₂₂ = 1;

Отсюда последовательно находим t₁₁ = 1;t₂₁ = –1/2;t₃₁ = 0;t₂₂ = 1/2;t₃₂ = –1/3;t₃₃ = 1/3, следовательно

А^–1=. (42)

Перемножив (42) и (40) получим (39).

Известно, что любая произвольная матрица Аможет быть представлена в виде двух треугольных.

Например, пусть имеется матрица

. (43)

Будем искать Т₁ =иТ₂ =. Диагональ в матрицеТ₂искусственно берется равной 1. Тогда

A = T₁  T₂ . (44)

Реализуя (44) и сравнивая с (43), получим

=.

Сравнивая значения правой и левой частей и выполняя простейшие вычисления, очевидно:

t₁₁ = 1; t₁₁ r₁₂ = –1; t₁₁ r₁₃ = 2;

t₂₁ = –1; t₂₁ r₁₂ + t₂₂ = 5; t₂₁ r₁₃+ t₂₂ r₂₃ = 4;

t₃₁ = 2; t₃₁ r₁₂ + t₃₂ = –1; t₃₁ r₁₃+ t₃₂ r₂₃ + t₃₃ = 14;

Решив полученную систему, получим

t₁₁ = 1; t₂₁ = –1; t₃₁ = 2;

t₂₂ = 4; t₃₂ = 6; t₃₁ = 1;

r₁₂ =–1; r₁₃ = 2; r₂₃ = 3/2.

Таким образом Т₁ =иТ₂ =, тогдаA^–1 = .

2.5. Применение метода итераций для уточнения элементов обратной матрицы

Точность получения элементов обратной матрицы естественно оценивается соотношением

А^–1А =А⁰ =Е.

Однако в общем случае элементы обратной матрицы получаются с некоторой погрешностью, которая появляется в результате округлений в процессе вычисления и большого числа арифметических операций. Для уменьшения погрешностей используется итерационнаясхема уточнения элементов обратной матрицы.

Пусть для неособенной матрицы Аполучено приближенное значение элементов матрицыА^–1. Обозначим ее черезD₀A^–1. Тогда для уточнения элементов обратной матрицы строится следующий итерационный процесс:

F_k–1 = E–AD_k–1 , k =1,2,3… ; (*)

D_k = D_k–1(E + F_k–1); k = 1,2,3… (**)

Доказано, что итерации сходятся, если начальная матрица D₀достаточно близка к искомойА^–1.

В данной итерационной схеме матрица Fна каждом шаге как бы оценивает близость матрицыDкА^–1.

Схема работает следующим образом.

Сначала по (*) при k = 1 находитсяF₀=E–AD₀, затем находится произведениеD₀F₀.

По итерации (**) при k= 1 находитсяD₁ =D₀+ D₀F₀.

Чтобы проверить, достигнута ли желаемая точность, вычисляется AD₁, а по (*) приk = 2, вычисляетсяF₁=E –AD₁ и, если наибольший элемент матрицыF₁ <, итерации прекращаются иA^–1D₁.