4.2.2. Общий случай построения итерирующих функций

Рассмотрим вариант построения итерирующих функций вида (4) для системы (3) с соблюдением условий (6). Напишем их в следующем виде:

₁(х,у) =;

₂(х,у) =;

При этом должно выполняться . Коэффициентынаходятся из решения следующей системы линейных уравнений, которая составлена по требованиям (6):

(7)

При таком подборе параметров условие (6) будет соблюдено, если частные производные функцийF₁ иF₂изменяются не очень быстро в окрестности точки (x₀,y₀).

Пример:

при х₀ = 0,8 иу₀ = 0,55. Для решения будем искать итерирующие функции в виде:

Составим систему (7). Предварительно определим компоненты системы (7) для x₀= 0,8;y₀= 0,55

;;

;;

;;

;–1.

Тогда система (7) имеет вид:

1+1,6+1,92=0=–0,3

1,1–=0=–0,5 ее решение.

1,6+1,92=0=–0,3

1+1,1–=0=0,4

Следовательно, итерирующие функции имеют вид:

и по (5) строим итерационный процесс.

4.3. Метод Ньютона для систем двух уравнений

Пусть дана система

Согласно методу Ньютона последовательные приближения типа (5) вычисляются по формулам

;,

где

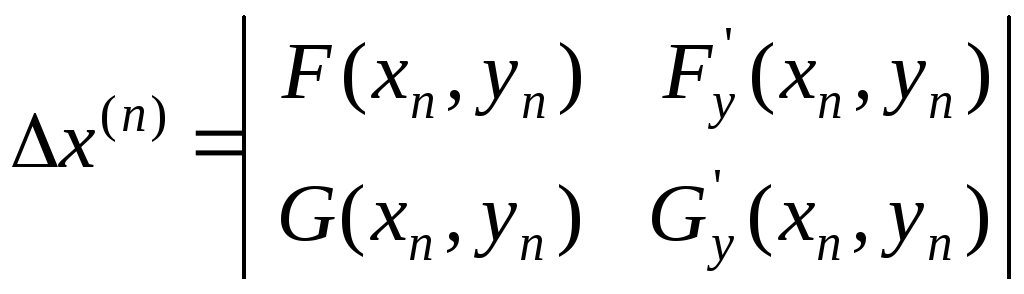;;n= 0,1,2, ...

и, если Якобиан

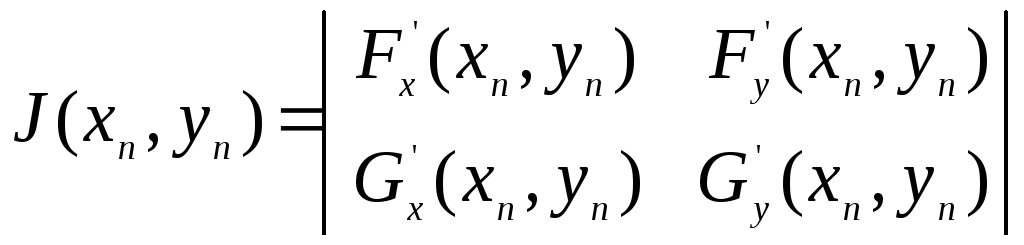 0

решение будет единственным.

Начальные значения x₀иy₀определяются грубо (приближенно – графически или «прикидкой»). Данный метод эффективен только при достаточной близости начального приближения к истинному решению системы.

Пример. Найти корни системы

Графическим путем можно найти приближенно x₀= 1,2 иy₀= 1,7.

.

В начальной точке

= 97,910.

По формулам получаем

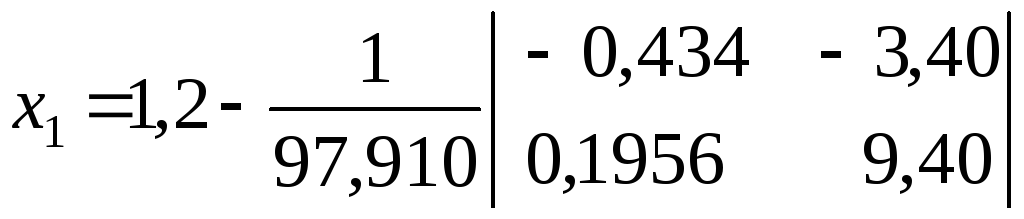= 1,2 + 0,0349 = 1,2349;

= 1,7 – 0,0390 = 1,6610.

Продолжая процесс вычисления при x₁иy₁, получимx₂= 1,2343;y₂= 1,6615 и т.д. до достижения желаемой точности.

4.4. Метод Ньютона для системn-го порядка сnнеизвестными

Для метода Ньютона функции F_i = (x₁,x₂, ...,x_n) из (1) раскладываются в ряд Тэйлора с отбрасыванием производных второго и выше порядков.

Пусть известен результат предварительной итерации при решении (1) дает результат для = (a₁,a₂, ...,a_n).

Задача сводится к нахождению поправок этого решения: x₁,x₂, ...,x_n.

Тогда при очередной итерации решение будет:

x₁ = a₁ + x₁; x₂ = a₂ + x₂; …, x_n = a_n + x_n. (8)

Для нахождения x_iразложим F_i(x₁,x₂, ...,x_n) в ряд Тейлора:

(9)

Приравняем правые части согласно (1) к нулю и получим систему линейных уравнений относительно x_i:

(10)

Значения F₁,F₂, …,F_nи их производных вычисляются приx₁=a₁,x₂=a₂, ...,x_n=a_n. Расчет ведется с учетом (8) по (9) и (10). Процесс прекращается, когдаmax|x_i| <. При этом будет иметь место единственное решение системы, если Якобиан

.

По сходимости этот метод выше метода простой итерации.

Раздел 5. Аппроксимация функций

5.1. Постановка задачи

При решении многих практических задач часто приходится вычислять значения каких-то функциональных зависимостей y=f(x).

При этом, как правило, имеют преобладающее место две ситуации.

1. Явная зависимость между хиyна [a,b] отсутствует, а имеется только таблица экспериментальных данных {x_i,y_i},и возникает необходимость определенияy=f(x) на интервале [x_i,x_i/2][a,b]. К этой задаче относится также уточнение таблиц экспериментальных данных.

2. Зависимость y=f(x) известна и непрерывна, но настолько сложна, что не пригодна для практических расчетов. Стоит задача упрощения вычисления значенийy=f(x) и ее характеристик (и т.д.). Поэтому, с точки зрения экономии времени и материальных ресурсов, приходят к необходимости построения какой-то другой функциональной зависимостиy =F(x), которая была бы близка кf(x) по основным ее параметрам, но более проста и удобна в реализации при последующих расчетах, т.е. ставится задача о приближении (аппроксимации) в области определенияy =f(x). Функциюy =F(x) называют аппроксимирующей.

Основной подходк решению данной задачи заключается в том, чтоy=F(x) выбирается зависящей от каких-то свободных параметров эксперимента, т.е.y =F(x) =(x,c₁,c₂, …,c_n) =(x,). Значения векторавыбираются из каких-то условий близости дляf(x) иF(x).

Bзависимости от способа подбора вектора, получают различные виды аппроксимации.

Если приближение строится на каком-то дискретном множестве {x_i},i=, то аппроксимация называетсяточечной. К ней относится интерполирование, среднеквадратичное приближение (МНК). Если множество {x_i} непрерывно, например, в виде отрезка [a,b], аппроксимация называетсянепрерывнойили интегральной (полиномы Чебышева).

В настоящее время на практике хорошо изучена и широко применяется линейная аппроксимация, при которой (x,) выбирается линейно-зависящий от параметровв виде так называемогообобщенного многочлена:

F(x) = (x,) = c₁₁(x) + c₂₂(x) + … + c_n_n(x) = ; (1)

здесь _k(x) – какая-то выбранная линейно-независимая система базисных функций. В качестве их могут быть, например,

– алгебраическая: 1, x,x², ...,xⁿ, ...;

– тригонометрическая: 1, sin(x),cos(x),…sin(nx),cos(nx),…;

– экспоненциальная: e^0x,e^1x, …,e^nx, …;

где {_i} – некоторая числовая последовательность попарно различных действительных чисел.

Важным является, чтобы эта система была полной, т.е. обеспечивающей аппроксимацию посредством (1) cзаданной точностью на всех интервалах [а,b] определенияy=f(x).

Для большинства практических задач наиболее удобна первая из них, представляющая собой в итоге обычные алгебраические многочлены.