4. Другие оценки погрешности

1. Приближенной оценкой погрешности могут быть:

– для трапеции и прямоугольника;

– для формулы Симпсона.

2. Следует заметить, что эмпирические формулы (25), (26), (28) предполагают и автоматическое изменение шага интегрирования h. Для этой цели имеется другая схема расчета, заключающаяся в следующем.

Анализ составных формул I_П,I_Т,I_Споказывают, что точное значение интеграла находится междуI_Ср.П(формула средних) иI_Т, при этом имеет место соотношение:

I_С= (2I_Ср.П +I_Т)/3. (29)

Соотношение (29) используется и для контроля погрешности вычисления. Если │I_С –I_Т│ ≥ ε, то шаг уменьшают вдвое и расчет повторяют. Если точность достигнута, то окончательное значение интеграла и получают по формуле (29).

6.5. Составные квадратурные формулы с переменным шагом

Проиллюстрируем решение данной проблемы на примере квадратурной формулы прямоугольников.

Пусть f(x)C²[a,b] с дополнительным ограничением:f"(x) – монотонная знакоопределенная функция на [a,b]. Для определенности возьмемf"(x) – монотонно убывающую положительную функцию.

EMBED Word.Picture.8

Положим x₀ =a. Определим наибольшее значениеx₁из условия (23), т.е. чтобы погрешность для

;·f"() =;; (30)

не превышала заданной величины . Очевидно, что для этого достаточно решить (24) относительноx₁.

Имеем x₁ =.

Следующие интервалы определяются аналогично.

Из рисунка видно, что длина последующих интервалов будет возрастать. Общая формула их определения такова:

x_i+1 = ; 0  i  k . (31)

Количество интервалов kнеизвестно, т.к. оно определяется как точностью, так и поведениемf"(x) на интервале [a,b]. Однако верхняя оценка дляkможет быть легко определена по длине наименьшего частичного интервала:

k .

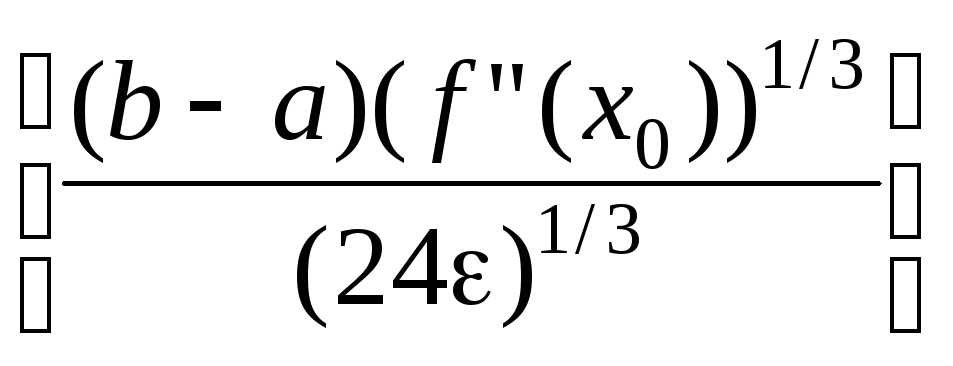Суммируя (30) получим составную квадратурную формулу прямоугольников с переменным шагом:

;

где x_iопределяется рекуррентно формулами (31). Для погрешностиRимеет место оценка |R|k.

В общем случае для произвольной функции f(x), еслиf"(x) – монотонно возрастающая положительная функция, то частичные интервалы определяются справа налево, т.е. отbкa. Для отрицательной производнойf"(x) и монотонно возрастающей – слева направо отaкb, для убывающей – справа налево отbкa.

В качестве иллюстрации рассмотрим интегрирование f(x) =e^–x/,= 10^–2с точностью= 10^–4на каждом частичном интервале, принадлежащем отрезку [0;1]. По (31) определим границы интервалов:

x₀ = 0,0000;x₁ = 0,0062;x₂ = 0,0138;x₃ = 0,0237;x₄ = 0,0374;

x₅ = 0,0590;x₆ = 0,1030;x₇ = 0,2990;x₈ = 1,0000.

Общая погрешность имеет оценку R810^–4. Такую погрешность посредством формулы прямоугольников сh=constможно получить, если выбирать шагhна всем интервале из условия=R, на 721-м частичном интервале:

K= .

В общем случае, если f"(x) на всем интервале [a,b] не удовлетворяет принятому дополнительному ограничению, то

– сначала следует интервал [a,b] разбить на частичные интервалы, на которыхf"(x) монотонна и знакоопределена;

– затем на каждом из них построить составную квадратурную формулу с переменным шагом по приведенным выше формулам.

EMBED Word.Picture.8

Аналогичные рассуждения имеют место и для формулы Симпсона с соблюдением монотонности f ^IV(x).

Однако следует заметить, что переход к переменному шагу hне всегда оправдан из-за необходимости вычислятьf"(x) и определять ее монотонность и знакоопределенность. Это бывает оправданным только при серийных расчетах.