§1. Уравнения Коши п. 1.1. Функциональное уравнение линейной однородной функции

Одним из наиболее исследованных в математике является функциональное уравнение Коши

f(x+y) = f(x) +f(y), D (f) =R (4)

Нетрудно заметить, что линейные однородные функции вида

f(x) = ax (a = const)

удовлетворяют этому уравнению:

f(x+y ) = a(x+y) = ax + ay = f(x) + f(y)

Вопрос состоит в том, будут ли эти функции единственными.

Прежде всего, выведем несколько общих фактов, не накладывая никаких ограничений на функцию f (т. е. без всяких предположений о непрерывности, ограниченности и т. п.).

Положим в уравнении y = x, получим:

f(2x) = 2f(x).

Далее, последовательно полагая y = 2x, y = 3x, y = 4x и т. д., имеем:

f(3x) = f(x+2x) = f(x)+f(2x) = f(x)+2f(x) = 3f(x);

f(4x) = f(x)+f(3x) = 4f(x);

f(5x) = f(x)+f(4x) = 5f(x),

и вообще, для любого натурального n

f(nx) = n·f(x) (1.1)

(это легко проверяется по индукции). Заменив здесь x на , мы получим

,

а затем, если подставить mx (m - натуральное) вместо x и использовать предыдущее равенство, придём к соотношению

, (1.2)

Положим теперь в основном уравнении (4) x = y = 0; получим

f(0) = 2f(0), так что f(0) = 0. (1.3)

Если же взять y = -x, то:

0 = f(x - x) = f(x) + f(-x)

f(-x) = -f(x),

так что функция f(x) является нечётной. А тогда из (1.1) легко вывести:

(1.4)

Полученные соотношения (1.2) – (1.4) могут быть объединены в равенстве

f(rx) = r·f(x),

справедливом для любого вещественного значения x, каково бы ни было рациональное число r.

Если взять здесь x = 1, то получим

f(r) = r·f(1) (1.5)

или, если обозначить f(1) через a, f(r) = ar.

Таким образом, мы, собственно говоря, установили уже вид функции f, но пока лишь для рациональных значений аргумента. При этом мы использовали только тот факт, что функция удовлетворяет основному уравнению Коши (4). Далее в решении мы будем уже опираться на конкретный класс функций, в котором ищется решение. Рассмотрим некоторые наиболее общие классы функций.

П. 1.1.1 Класс непрерывных функций

Для рациональных x мы установили, что f(x) = ax. Осталось показать, что это соотношение справедливо и для иррациональных x. Пусть x будет любое иррациональное число. Тогда существует последовательность рациональных чисел

,

сходящаяся к этому числу x (это известный факт; можно, например, взять отрезки соответствующей бесконечной десятичной дроби). По доказанному

f(r_n) = ar_n (n = 1,2,3, . . .).

Перейдём здесь к пределу при

Справа мы получим ax, слева же, именно ввиду предположенной непрерывности функции f, получится

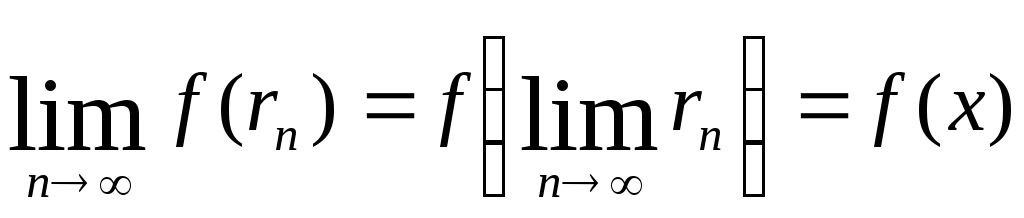
так что, окончательно,

f(x) = ax.

Таким образом, действительно, все непрерывные аддитивные функции являются линейными однородными. Последняя формула даёт самое общее решение функционального уравнения (4).

П. 1.1.2 Класс монотонных функций.

Здесь мы будем предполагать, что функция f не убывает на всей действительной оси (случай невозрастания функции рассматривается аналогично). Значит для любых x₁ < x₂.

Для рациональных x доказано f(x) = x·f(1). Возьмём произвольное иррациональное x. Известно, что любое иррациональное число можно сколь угодно точно приблизить рациональными числами, поэтому для любого натурально q существует целое p такое, что

(1.6)

и при достаточно больших q число x расположено между двумя очень близкими рациональными числами, разность между которыми равна . Используя монотонность функции f, находим

откуда (воспользовавшись соотношением для рациональных значений функции f)

, a = f(1). (1.7)

Так как из (1.3) f(0) = 0, то, ведь функция f не убывает, значит,.

Если a = 0, то из неравенств имеем .

Если a = 0, то из (1.7)

. (1.8)

Сравнивая эти неравенства с (1.6), получим

Покажем это. Предположим, что это неверно, например,

для выбранного иррационального x. Подберём q настолько большим, чтобы дробь попала междуиx

что противоречиво с (1.8). Полученное противоречие показывает, что

для любого заданного иррационального x, поэтому f(x) = ax для всех x.

п. 1.1.3 Класс ограниченных функций.

Пусть теперь функция f(x) ограничена с одной стороны (т. е. ограничена либо сверху, либо снизу) на каком-либо интервале (a, b). Нам нужно доказать, что линейными однородными функциями исчерпываются все решения (4) в данном классе. Мы исследуем решение уравнения (4), предполагая f ограниченной сверху (случай, когда f ограничена снизу, сводится к рассматриваемому случаю заменой f на -f).

Будем считать, что функция f ограничена сверху константой M, т. е. для всех. Рассмотрим вспомогательную функцию

g(x) = f(x) - x·f(1).

По доказанному выше g(x) = 0 при любом рациональном x. Кроме того, функция g(x) также является аддитивной. Действительно,

g(x + y) = f(x + y) - (x + y)·f(1) = f(x) + f(y) - xf(1) - yf(1) = g(x) + g(y).

Подставим y = r (r - рациональное) в равенство

g(x+y) = g(x)+g(y),

получим, учитывая g(r) = 0,

g(x+r) = g(x)+g(r) = g(x).

Значит, любое рациональное число r является периодом функции g(x).

Покажем теперь, что g(x) ограничена на интервале (a, b). Имеем

где , поскольку при .

Отсюда тогда следует, что g(x) ограничена сверху на всей вещественной оси. В самом деле, для любого действительного x существует рациональное число r такое, что r (a-x, b-x), т. е. a < x+r < b. Поэтому

g(x) = g(x+r) < M1,

так как x + r (a, b), а на интервале (a, b) функция g ограничена числом M₁.

Сейчас уже можно утверждать, что g(x) = 0 для любого действительного x. Допустим это не так, т. е. для некоторого x₀

g(x₀) = A, A 0.

Поскольку для функции g(x), как для любой аддитивной функции, верно соотношение (1.1), то

g(nx₀) = ng(x₀) = nA

для любого целого n. Очевидно, что можно подобрать такое n (может быть, достаточно большое по абсолютной величине), что

nA > M₁, т.е. g(nx₀) > M₁.

Но функция g ограничена сверху константой M₁. Получаем противоречие. Значит, g(x) 0, откуда f(x) = x·f(1), что и требовалось.