§ 3. Метод подстановок

Заменяя некоторые переменные функционального уравнения либо конкретными значениями, либо какими-либо другими выражениями пытаемся либо упростить это уравнение, либо привести его к такому виду, что дальнейшее решение станет очевидным. Особенность применяемого метода как раз и состоит в том, что в ряде случаев он позволяет отыскать решения в классе всевозможных функций. Поясним метод на следующих примерах.

Пример 8. Найти все решения функционального уравнения

f(xy) = y^k f(x), k N.

Решение. Положим в уравнении x = 0: f(0) = y^k f(0). Так как y - произвольно, то f(0) = 0.

Пусть теперь x ≠ 0. Подставим в уравнение , получим:

или (a=f(1))

Функция f(x) = ax^k является решением исходного уравнения.

Пример 9. Пусть - некоторое действительное число. Найти функциюf(x), определённую для всех x ≠ 1 и удовлетворяющую уравнению

,

где g – заданная функция, определённая при x ≠ 1.

Решение. При замене

получаем систему

.

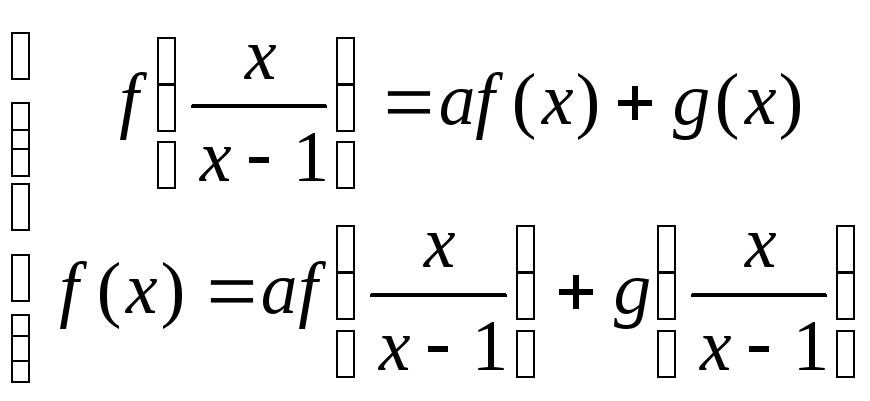решением которой при a² ≠ 1 является функция

Пример 10. Найти все функции f(x), заданные на промежутке , для которых выполнено равенство

Решение. Выполнив последовательно две замены

приходим к системе функциональных уравнений:

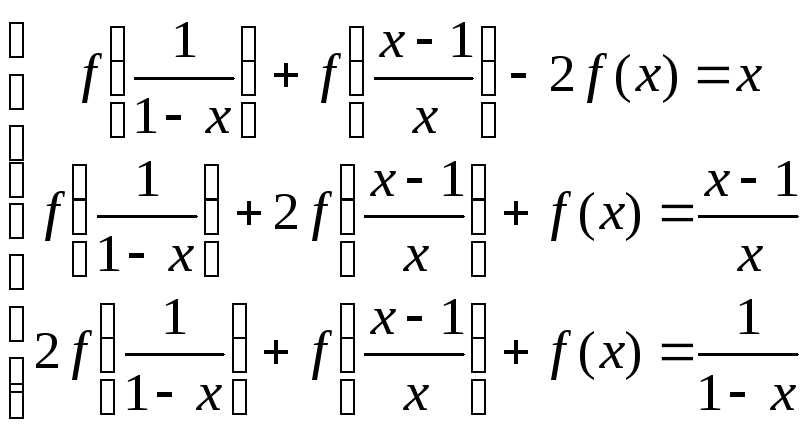
Последнее уравнение есть сумма первых двух, умноженных на -1, т. е. из данной системы функция f(x) однозначно не определяется. Из первых двух уравнений находим

Мы можем определить f(x) произвольным образом на одном из интервалов и эти формулы дадут нам расширениеf(x) на вcё множество I.

Пример 11. Найти решение системы функциональных уравнений относительно неизвестных функций f(x) и g(x):

Решение. В первом уравнении сделаем подстановку 2x = 1/z.

При этом

и первое уравнение принимает вид:

или

В результате получаем систему уравнений:

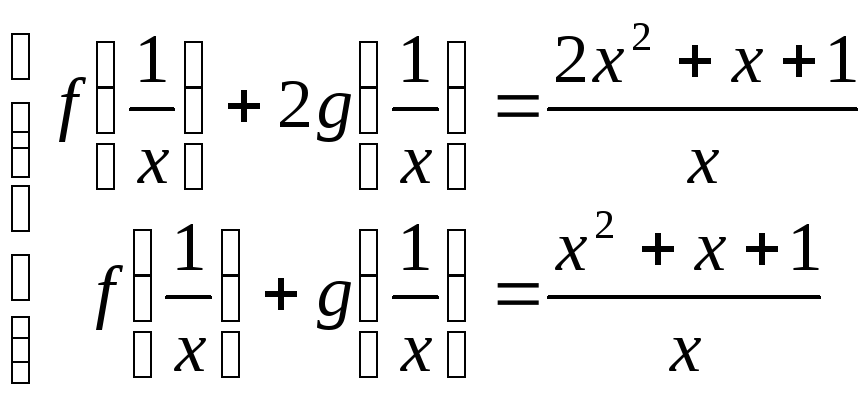
решение которой g(x) = 1/x, f(x) = x+1.

§ 4. Решение функциональных уравнений с применением теории групп

В уравнении под знаком неизвестной функцииf(x) стоят функции g₁ = х и g₂ = а – х. В результате замены х на а – х получено еще одно уравнение, содержащее те же функции f (х) и f (а – х). Функции g₁ и g₂ образуют группу относительно композиции функций. Понятие группы позволяет в ряде случаев выбрать целесообразные подстановки для решения функциональных уравнений.

Пусть в функциональном уравнении

(4.1)

выражения f₀(x) = x, f₁(x), …, f_n-1(x), стоящие под знаком неизвестной функции g (x), являются элементами конечной группы порядка n относительно композиции функций. Коэффицненты уравнения (4.1) а₀, а₁ ..., а_n-1, b в общем случае зависят от x. Некоторые из них могут равняться 0. Предположим, что уравнение (4.1) имеет решение. Заменим х на f₁(x). Эта замена равносильна умножению справа всех элементов группы f₁. В результате последовательность функций f₀, f₁, …, f_n-1перейдет в последовательность , состоящую из всех элементов группы.

Произведенная замена перевела уравнение (4.1) —линейное относительно неизвестных g(f₀), g(f₁), …,g( f_n-1) — в новое линейное уравнение относительно тех же неизвестных. Заменяя далее x → f₂(x), x → f₃(x),…, x → f_n(x) получим систему n линейных уравнений с n неизвестными.

Решая эту систему, находим неизвестную функцию g(f₀) = g(x), если, конечно, система имеет решение. Непосредственной проверкой следует убедиться, что полученная функция удовлетворяет исходному уравнению. Рассмотренный метод ограничивает область определения функции, так как приходится отбрасывать те значения аргумента, при которых элементы группы не имеют смысла.

Пример 12. Найти функцию f (х), определенную на множестве действительных чисел, отличных от 0, 1, –1, и удовлетворяющую уравнению

(4.2)

Решение. Выражения , стоящие под знаком неизвестной функцииf, являются элементами группы, заданной таблицей:

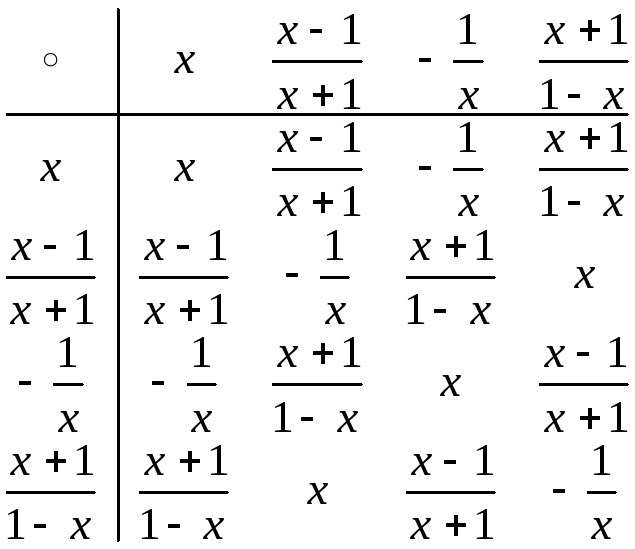
Заменяя последовательно х на,,, получим систему

Последовательно исключая неизвестные ,,, имеем

Рассуждения вытекали из предположения, что решение урав­нения (4.2) существует. Подставляя в (4.2) полученную функцию, убедимся, что она удовлетворяет уравнению.

Пример 13. Найти функцию f(x), х ≠ 0, х ≠ а, удовлетво­ряющую уравнению

где а — постоянная, отличная от 0.

Решение. Нетрудно проверить, что выражения х,, вместе с составляют группу с таблицей:

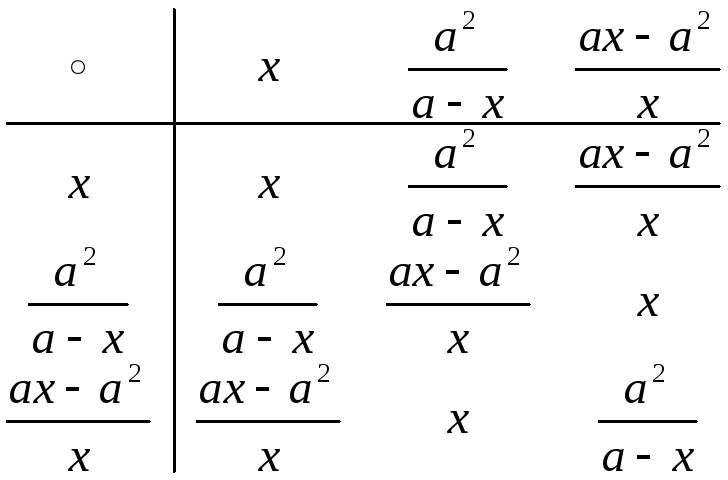
Здесь xR\{0, а}.

Рассуждая аналогично решению примера 12, получим систему

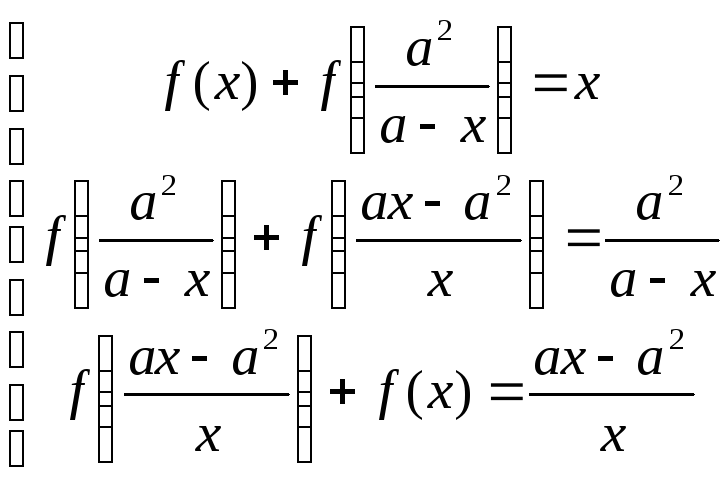
из нее находим . Проверка показывает, что эта функция удовлетворяет уравнению.

Иногда в функциональном уравнении выражения, стоящие под знаком неизвестной функции, являются значениями элементов некоторой группы от одной и той же функции g. После замены g(x) на x получаем уравнение, которое решается изложенным выше методом.

Рассмотрим функциональные уравнения, в которых под знаков неизвестной функции стоят, кроме выражений, зависящих от х, и константы.

Пример 14. Решить уравнение

(4.3)

Решение. На множестве {х, 1, –х, 1, 0} определена операция композиции, если рассматривать числа 1 и 0 как функции, тождественно равные константе. Таблица умножения здесь имеет вид:

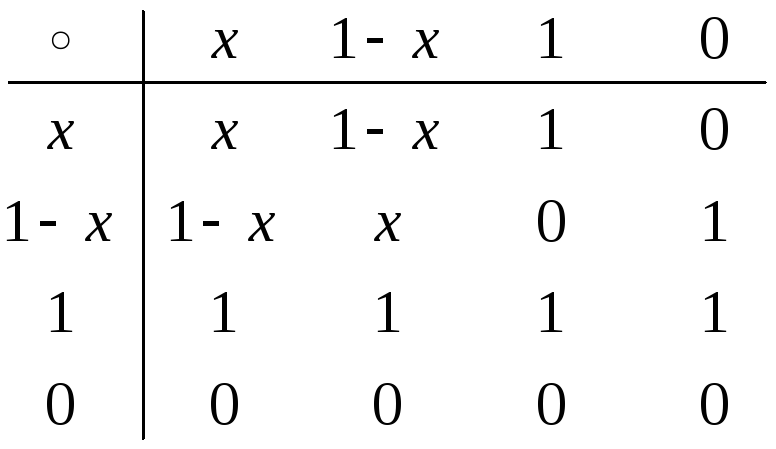
Из таблицы видно, что для элементов 1 и 0 не существует обратных, т. е. данное множество функций не является группой. В алгебре множества с ассоциативной операцией называют полугруппами. Полугруппы в отдельных случаях можно применить к решению функциональных уравнений.

Делая в (4.3) последовательно замены х → 1 – х, x → 1, x → 1 получим систему

Из двух последних уравнений имеем .

Теперь из первых двух уравнений найдем: . Проверка показывает, что найденная функция удовлетворяет уравнению (4.3).