П.1.3. Функциональное уравнение логарифмической функции

Все непрерывные решения функционального уравнения

f (xy) = f(x) + f(y), (6)

справедливого для всех положительных значений x и y, имеют вид

f(x) = log_a x (a > 0, a 1).

Докажем это. Для этого введём новую переменную ξ, изменяющуюся в промежутке (-; +), и положим

x = eξ (ведь x > 0), φ(ξ) = f(e^ξ),

откуда

ξ = lnx, f(x) = φ(lnx).

Тогда функция φ удовлетворяет функциональному уравнению (4):

а потому

и f(x) = clnx.

Если исключить случай c = 0 (тогда f(x) 0), то полученный результат может быть написан в виде

f(x) = log_a x, a = e^1/c.

П.1.4. Функциональное уравнение степенной функции

Функциональному уравнению

f(xy) = f(x)·f(y) (x > 0, y > 0) (7)

удовлетворяют в классе непрерывных функций только функции вида

f(x) = x^a.

Прибегая к той же подстановке, что и в п. 1.3, мы приведём уравнение (7) к уравнению (4):

,

откуда

φ(ξ) = c^ξ (c >0), и, значит, f(x) = c^lnx = x^a (a = lnc).

Метод последовательного анализа можно применить к решению других уравнений.

Пример 1. Функция f определена и непрерывна на множестве R, f(1) = 1 и для любых действительных x и y

Чему равно f(x)?

Решение. Из данного равенства при x = y = 0 получаем, что f(0) = 0, а при y = 0 имеем f(x) = f(|x|), так что функция f чётная и достаточно рассматривать только положительные значения аргумента.

По индукции легко получить равенство

;

в самом деле, по предположению индукции

Положив в доказанном равенстве

,

будем иметь

,

т.е.

.

Если теперь – положительное рациональное число, то

,

если же x - иррациональное число, то x является пределом последовательности рациональных чисел, , и в силу непрерывностиf будем иметь

П.1.5. Одно обобщение уравнения Коши.

Пусть n — фиксированное натуральное число. Рассмотрим функциональное уравнение

(1.11)

где D (f) = R. При n = 1 оно обращается в уравнение Коши. Как было показано, в классе непрерывных функций единственным решением уравнения Коши является линейная однородная функция. Из результатов Гамеля следует, что и разрывные функции могут удовлетворять уравнению Коши. Покажем, что решение уравнения (1.11) при n > 1 является непрерывной функцией.

Полагая х = у = 0, получим f (0) = 0. Поэтому при х = 0 из (1.11) имеем f(уⁿ) = (f(y))ⁿ для всех у R. Каждое неотрицательное число z может быть записано в видеz = уⁿ. Отсюда

В частности, при х = -z

т. е. f(-z) = - f (z), z R. Если , то

Отсюда следует что f(х + w) = f(х) + f(w) для всех х R,w R, т. е.f(х) — аддитивная функция. Для аддитивной функции при рациональных t имеет место соотношение f(tw) = tf (w). Легко видеть, что

(1.12)

Воспользовавшись формулой Ньютона

,

и аддитивностью f(x), преобразуем отдельно левую и правую части (1.12) при рациональных t:

;

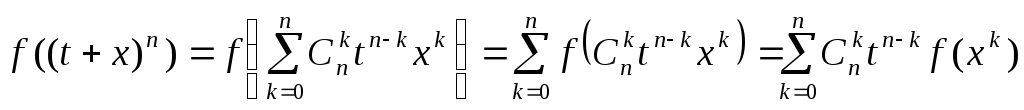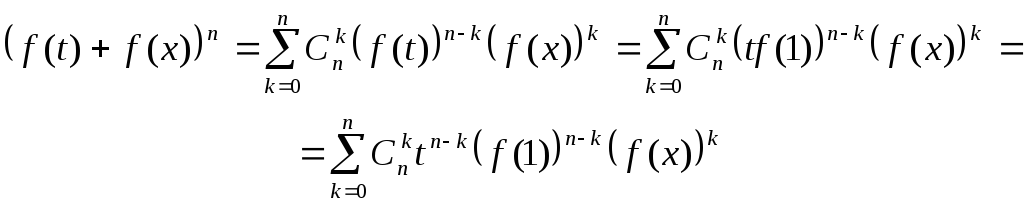
Правые части последних двух равенств представляют собой многочлены от t. Приравнивая коэффициенты при одинаковых степенях t, получим

, .

В частности, для k = 2 имеем

. (1.13)

Если (f(1))^n-2 > 0, то f(x) — неубывающая функция. Действительно, всякое у > 0 представимо в виде у = х², поэтому из (1.13) имеем f(у) = f(x²) ≥ 0. При х₁ > x₂, х₁ – x₂> 0, f(x₁ – x₂) ≥ 0, или, в силу аддитивности f(х), f (x₁) – f (х₂) ≥ 0. Если же (f(1))^{n -2} < 0, аналогично доказывается, что функция f(х) — невозрастающая.

Ранее было доказано, что если аддитивная функция монотонна, то она имеет вид f(х) = ах.

Полагая в (1.13) х = 1, получим, что f(1) равно 0 или 1 при четном n и f(1) равно 0, 1 или -1 при нечетном n > 1.

Итак, f (х) = х либо f(х) = 0 при четных n; f (x) = х, либо f (х) = -х, либо f(х) = 0 при нечетных n > 1.

Тем самым доказана не только непрерывность решения уравнения (1.11) при n > 1, но и получен его вид.