
- •Содержание Введение
- •§1. Уравнения Коши п. 1.1. Функциональное уравнение линейной однородной функции
- •П. 1.1.1 Класс непрерывных функций
- •П. 1.1.2 Класс монотонных функций.
- •П.1.1.4. Класс дифференцируемых функций.
- •П.1.2. Функциональное уравнение показательной функции
- •П.1.3. Функциональное уравнение логарифмической функции
- •П.1.4. Функциональное уравнение степенной функции
- •П.1.5. Одно обобщение уравнения Коши.
- •§ 2. Метод сведения функционального уравнения к известному уравнению с помощью замены переменной и функции
- •§ 3. Метод подстановок
- •§ 4. Решение функциональных уравнений с применением теории групп
- •§ 5. Применение теории матриц к решению функциональных уравнений
- •§ 6. Применение элементов математического анализа к решению функциональных уравнений п. 6.1. Предельный переход
- •П. 6.2. Дифференцирование
- •Заключение
- •Список литературы
§ 6. Применение элементов математического анализа к решению функциональных уравнений п. 6.1. Предельный переход
Идею предельного перехода проиллюстрируем на следующих примерах.
Пример 17. Решить в классе непрерывных функций уравнение
![]() (6.1)
(6.1)
где х
![]() R.
R.
Решение.
Заменив
х на
![]() ,
получим
,
получим
![]() (6.2)
(6.2)
Используя ту же замену, из уравнения (6.2) последовательно получим
![]() ,
,
![]() ,
,
……………………………………..
Методом математической индукции можно доказать, что
![]() (6.3)
(6.3)
Сложив все уравнения, начиная с (6.2), получим
![]() (6.4)
(6.4)
Так как функция f(х) непрерывна, то при любом фиксированном х
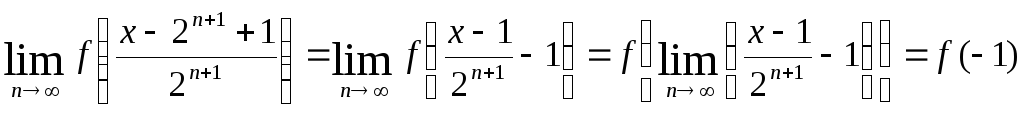
Здесь
![]() .
Из (6.1)
.
Из (6.1)
![]() .
Тогда
.
Тогда
![]()
Левая часть равенства (6.4) не зависит от n, поэтому существует ее предел при n → ∞. Переходя к пределу в равенстве (6.4), при n → ∞ имеем
![]() (6.5)
(6.5)
Правая часть (6.5) является суммой трех бесконечно убывающих прогрессий
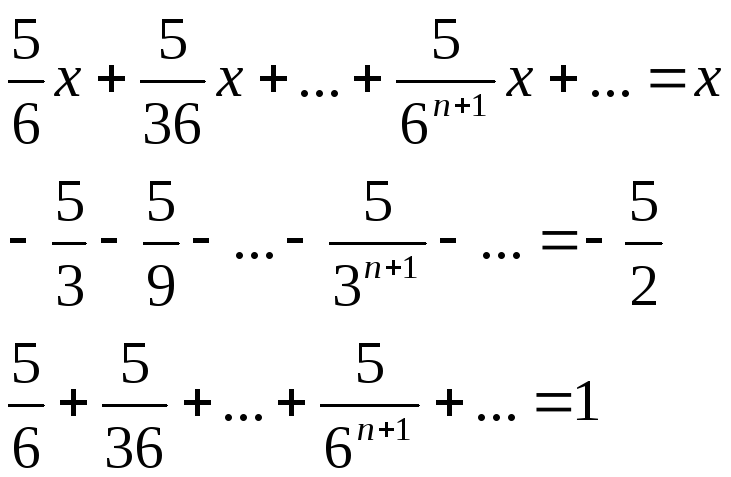
Итак,
![]() ,
что и подтверждается проверкой.
,
что и подтверждается проверкой.
Пример
18. Функция
f:
R→R
непрерывна в точке 0 и для любого x
![]() R
выполнено равенство
R
выполнено равенство
2f(2x) = f(x)+x.
Найти все такие f.
Решение. Пусть функция f удовлетворяет условию. Тогда
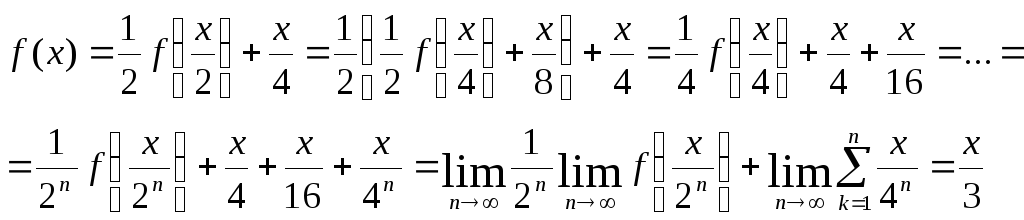
Тривиальная проверка показывает, что функция x/3 действительно является искомой.
Пример 19. Доказать, что уравнение
![]() ,
,
![]() (6.6)
(6.6)
не имеет непрерывных решений.
Решение. Допустим, что существует непрерывное решение функционального уравнения (6.6). Подставим в исходное уравнения вместо x выражение
![]()
ведь если x ≥ 0, то и
![]()
получим:
![]() (6.7)
(6.7)
Теперь сделаем такую же замену
![]()
в соотношении (6.7):
![]() (6.8)
(6.8)
Описанную операцию проделаем ещё несколько pаз. На n-ом шаге имеем:
![]()
Сложим все получившиеся выражения, начиная с (6.6) (всего будет n выражений), и приведем подобные слагаемые:
![]() (6.9)
(6.9)
Равенство (6.9) верно для любого натурального n. Зафиксируем x, а n устремим к ∞. Ввиду непрерывности f(x) в точке x = 0, находим
![]() (6.10)
(6.10)
где
![]()
В левой части (6.10) при конкретном (фиксированном) x стоит некоторая константа, т.е. при данном x ряд в правой части (6.10) сходится к этой константе. Мы же покажем, что этот ряд расходится для любого значения x > 0, таким образом, придём к противоречию.
Для любого натурального k и x > 0 верно неравенство
![]()
так что
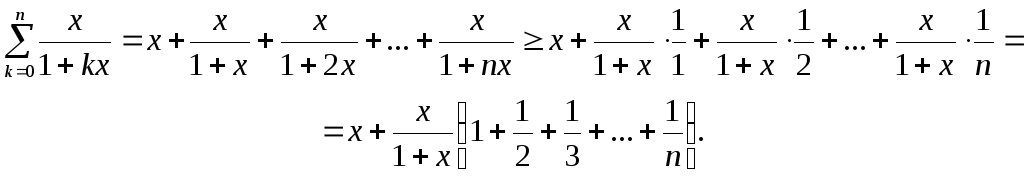
Гармонический ряд
![]()
неограниченно возрастает при увеличении n (известный факт), следовательно,
![]()
расходится к ∞. Что и требовалось доказать.
Пример 20. Найти f(x), ограниченную на любом конечном интервале, удовлетворяющую функциональному уравнению:
![]()
Решение.
x
= 0
![]() f(0)
= 0;
f(0)
= 0;

…………………………………………
![]()
![]()
переходя к lim при x → ∞ используя непрерывность f(x) и f(0) = 0 получаем, что
![]() .
.
Пример 21. Решить функциональное уравнение
![]() (6.11)
(6.11)
в классе непрерывных функций.
Решение.
Выполнив замену
![]() ,
получим
,
получим
![]() (6.12)
(6.12)
Складывая
(6.11) с уравнением (6.12), умноженным на
![]() ,
получим
,
получим
![]()
Это
уравнение решается аналогично уравнению
(6.1). Найдем подстановку, переводящую
![]() в
в![]() .
Для этого положим
.
Для этого положим
![]() .
Отсюда
.
Отсюда![]() .
Выполнивn
раз подстановку
.
Выполнивn
раз подстановку
![]() ,
получим систему уравнений, из которой
находим
,
получим систему уравнений, из которой
находим
![]()
Отсюда при n → ∞
![]() ,
или
,
или
![]() ,
,
что и подтверждается проверкой.
\
П. 6.2. Дифференцирование
В некоторых случаях для нахождения решения функционального уравнения целесообразно продифференцировать обе части уравнения, если, конечно, производная существует. В результате получим функциональное уравнение, которое содержит и производную неизвестной функции. Решим это уравнение относительно производной. Тогда неизвестная функция является одной из первообразных для найденной производной. Этот метод уже применялся при решении уравнения Коши в классе дифференцируемых функций.
Пример 22. Найти в классе функций, имеющих непрерывные производные, решение уравнения
f(3x+2)
= 3f(x), x
![]() R.
(6.13)
R.
(6.13)
Решение. Попытки решить уравнение методом предельного перехода не приводят к желаемому результату. Левая и правая части (6.13) являются функциями от х. Они равны, следовательно, равны их производные по х. Продифференцируем (6.13) и после сокращения получим
f′(3x+2) = 3f′(x)
Это
уравнение уже можно решить методом
предельного перехода. Выполнив подстановку
![]() ,
получим цепочку равенств
,
получим цепочку равенств
![]()
Ввиду
непрерывности ![]() ,
при n
→ ∞, имеем
,
при n
→ ∞, имеем
![]()
Итак,
![]() = k, где
k ===
= k, где
k === ![]() .
Первообразная функция f(х)
== kx + b.
Подставив в (6.13) х = –1, получим f(—1)
= 0.
Кроме того, f(–1)
= – k + b,
т. е. k
= b.
.
Первообразная функция f(х)
== kx + b.
Подставив в (6.13) х = –1, получим f(—1)
= 0.
Кроме того, f(–1)
= – k + b,
т. е. k
= b.
Легко проверить, что f (х) = k (х + 1) удовлетворяет условию при произвольном k.
Пример 23. Найти все действительные дифференцируемые функции, удовлетворяющие функциональному уравнению
![]() (6.14)
(6.14)
Решение. Пусть f удовлетворяет данному уравнению. Тогда
![]()
т.е. f(0)[1+f 2(x)] = 0, и, следовательно, f(0) = 0.
После преобразований имеем
![]() ,
(6.15)
,
(6.15)
откуда, с учётом
![]()
следует, что
f(x) = C (1+f 2(x)), (6.16)
где C = f′(0). Значит,
![]() ,
,
![]()
![]()
Условие f(0) = 0 означает, что C1 = 0, т.е. f(x) = tg Cx. Очевидно, все функции вида tg Cx подходят под условие задачи.
Пример 24. Найти функцию f(x), удовлетворяющую уравнению
f′(x)
+xf (-x) = ax
x
![]() R, a = const.
R, a = const.
Решение. f′(-x)-xf(x) = -ax. Введём новые функции
![]()
![]()
Ясно, что функция F(x) - чётная, а G(x) - нечётная функции, причём f(x) = F(x)+G(x). Получим уравнение относительно новых функций F(x) и G(x):
G′(x)-xG(x) = 0, F′(x) +xF(x) = ax,
![]()
![]()
Так как G(-x) = -G(x), то G(x) ≡ 0 и
![]()
Непосредственной проверкой убеждаемся в том, что при любых числах a, A функция f(x) является решением исходного уравнения.
