Контрольные вопросы

1. Изложите классический метод составления дифференциальных уравнений.

2. Назовите виды дифференциальных уравнений САР.

3. Дайте определение характеристическому полиному.

4. Назовите передаточные функции САР.

5. Опишите методику составления дифференциальных уравнений системы на основе типовых динамических звеньев.

5. Устойчивость линейных систем автоматического регулирования

5.1. Понятие об устойчивости линейных систем

Рассмотрим дифференциальное уравнение движения линеаризованной системы автоматического регулирования (4.7), записанное для регулируемой величины Х(t) при наличии управляющего воздействия Y(t) и равенстве нулю возмущающих воздействий

, (5.1)

где коэффициенты а₀– а_nи b₀– b_mпредставляют собой постоянные величины.

Степень оператора в правой части уравнения не может быть выше, чем в левой m ≤ n.

Дифференциальное уравнение движения системы регулирования можно записать для возмущающего воздействия F_K(t). В этом случае левая часть (5.1) остаётся без изменения, а правая часть будет иметь другой вид. В общем виде дифференциальное уравнение, определяющее изменение регулируемой величины, может быть записано так, что в правой его части будет находиться некоторая функция времениf(t). Характер переходных процессов в системе определяется видом левой части дифференциального уравнения (5.1). Поэтому для определения качественной картины переходных процессов практически безразлично записать ли исходное дифференциальное уравнение для управляющего или возмущающего воздействий.

Процесс регулирования определяется решением дифференциального уравнения как суммы двух решений – частного решения неоднородного уравнения (5.1) с правой частью и общего решения уравнения (5.1) без правой части, то есть с правой частью, равной нулю:

. (5.2)

Первое слагаемое (5.2) называют вынужденным решением(когда Х_частн(t) =const, это будет установившееся значение), а второе слагаемоепереходной составляющей

. (5.3)

Система будет называться устойчивой, если с течением времени при стремлении времени к бесконечностипереходная составляющая будет стремиться к нулю(приt  , Х_П(t)0). Найдем из (5.1) общее решение (переходную составляющую). Для этой цели необходимо решить дифференциальное уравнение (5.1) без правой части

. (5.4)

Общее решение выполняется в виде

. (5.5)

Дифференцируя выражение (5.5) nраз, подставляем его в (5.4) и после сокращения на общий множительCe^tимеем

. (5.6)

Это уравнение называется характеристическим.Корни его₁–_nбудут определять характер переходного процесса в системе. Нетрудно увидеть, что левая часть (5.6) полностью совпадает с левой частью (5.1) . Поэтому характеристическое уравнение получается приравниванием левой части (5.1) нулю:

. (5.7)

Однако здесь буква «p» означает не символ дифференцирования, а некоторое комплексное число, которое является решением характеристического уравнения.

Так как в решении характеристического уравнения содержится nкорней, то переходная составляющая (или общее решение), как известно, представляется в виде:

, (5.8)

где ₁–_n– корни характеристического уравнения; С₁– С_n – постоянные интегрирования, определяемые из начальных условий (управляющего воздействия и его производных).

Если корни характеристического уравнения определяются только видом левой части уравнения (5.1), то постоянные интегрирования определяются также и видом правой его части. Поэтому быстрота затухания и форма переходного процесса определяются как левой, так и правой частью исходного дифференциального уравнения.

Поскольку в понятие устойчивости системы входит только факт наличия или отсутствия затухания переходного процесса (независимо от быстроты затухания и формы переходного процесса), то устойчивость линейной системы совершенно не зависит от вида правой части дифференциального уравнения (5.1) и определяется только характеристическим уравнением.

Чтобы определить, устойчива система или неустойчива, нет необходимости полностью знать корни характеристического уравнения. Выясним, какие свойства корней необходимы и достаточны для того, чтобы система была устойчивой.

В

Рис. 5.1. Вещественные корни

общем виде корни любого уравнения могут быть вещественными, комплексными и чисто мнимыми. Рассмотрим эти случаи для характеристического уравнения.

1. Вещественный корень.Пусть один из корней, например₁, является вещественным. Если он отрицательный₁= –α₁, то слагаемое, определяемое этим корнем в (5.8) , будет представлять собой экспоненту. Очевидно, что приt  это слагаемое будет «затухать».

При ₁= +α₁получим не затухающий, а расходящийся процесс (рис. 5.1).

2. Комплексные корни.Комплексные корни бывают попарно сопряженными. При отрицательной вещественной части два корня, например₁и₂, будут иметь вид. В этом случае слагаемые, определяемые этими корнями в уравнении (5.8), могут быть представлены в виде:

, (5.9)

где A и – новые постоянные интегрирования.

Нетрудно увидеть, что мнимая часть корня представляет собой круговую частоту затухающих колебаний, а– показатель затухания огибающей к кривой переходного процесса (рис. 5.2,а). При положительной вещественной части два корня будут иметь види колебательный процесс будет не затухающим, а расходящимся (рис. 5.2,б).

3. Мнимые корни.В этом случае₁= +jи₂= –j. Слагаемые, определяемые этими корнями в (5.8), будут представлять собой незатухающие колебания, то есть колебания с постоянной амплитудой

. (5.10)

Такой процесс изображён на рис. 5.2, в.

Из анализа переходных процессов от корней различного вида можно сделать вывод, что для затухания переходного процесса необходимо, чтобы вещественные части корней были отрицательными. Это относится как к вещественным, так и к комплексным корням. Если хотя бы один корень характеристического уравнения будет иметь положительную вещественную часть, то переходный процесс в САР в целом будет расходиться, то есть система окажется неустойчивой.

К

Рис. 5.3. Граница устойчивости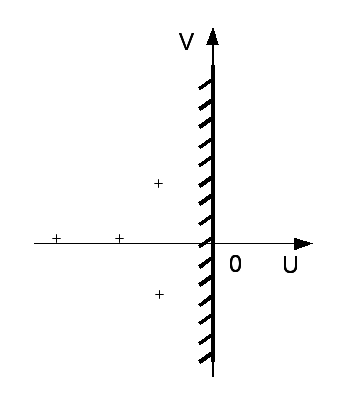

орни характеристического уравнения можно представить в виде точек на комплексной плоскости (рис. 5.3).

Для устойчивости линейной системы необходимо и достаточно, чтобы все корни лежали слева от мнимой оси плоскости корней. Если хотя бы один корень окажется справа от мнимой оси, то система будет неустойчивой.Таким образом, мнимая ось представляет собойграницу устойчивостив плоскости корней, за которую не должны переходить корни характеристического уравнения. Вся левая полуплоскость представляет собой при этомобласть устойчивости.

Превращение устойчивой системы в неустойчивую произойдет в том случае, если хотя бы один вещественный или пара комплексных корней перейдет из левой полуплоскости в правую. На границе перехода будем иметь так называемую границу устойчивости системы. Различают три типа границы устойчивости:

1) наличие нулевого корня;

2) наличие пары чисто мнимых корней;

3) наличие бесконечного корня.

Во всех трех случаях предполагается, что все остальные корни имеют отрицательные вещественные части.

В первом случае вещественный корень попадает на границу устойчивости (ось мнимых) в начале координат, то есть выполняется условие = 0. Это означает, что в характеристическом уравнении будет отсутствовать свободный член а_n= 0. Дифференциальное уравнение (5.1) в этом случае может быть записано в виде:

(5.11)

и система будет устойчивой не относительно регулируемой величины Х, а относительно скорости ее изменения рХ. Величина же отклонения регулируемой величины может принимать произвольные значения. Такую систему называют нейтрально устойчивой, имея в виду её безразличие к значению самой регулируемой величины.

На границе устойчивости второго типа, которая называется колебательной границей устойчивости, два корня попадают на мнимую ось. Система в этом случае будет иметь незатухающие гармонические колебания с постоянной амплитудой (рис. 5.2, в).

Наконец вещественный корень может попасть из левой полуплоскости в правую, проходя через бесконечность. В этом случае слагаемое в выражении (5.8) обращается в нуль, что соответствует понижению порядка дифференциального уравнения на единицу. Это будет при а₀= 0. Граница устойчивости третьего типа встречается очень редко.

Как было показано выше, ни одна реальная система автоматического регулирования не является строго линейной. Линейные характеристики звеньев и линейные дифференциальные уравнения можно получить путем линеаризации реальных характеристик и уравнений. При разложении в ряд Тейлора ограничиваемся линейными членами, отбрасывая члены высших порядков, которые для малых отклонений считали также малыми.

Обоснование законности такой линеаризации содержится в теоремах Ляпунова, которые даны без доказательства.

1. Если характеристическое уравнение линеаризованной системы имеет все корни с отрицательными вещественными частями, то реальная система будет также устойчивой, то есть малые нелинейные члены не могут в этом случае нарушить устойчивость системы.

2. Если характеристическое уравнение линеаризованной системы имеет хотя бы один корень с положительной вещественной частью, то реальная система будет также неустойчивой, то есть малые нелинейные члены не могут сделать её устойчивой.

3. При наличии нулевых и чисто мнимых корней поведение реальной системы не всегда даже качественно определяется её линеаризованными уравнениями. При этом даже малые нелинейные члены могут коренным образом изменить вид переходного процесса, сделав систему устойчивой или неустойчивой.

Опираясь в своих линейных расчетах на эти теоремы Ляпунова, всегда следует иметь в виду, что они, во-первых, относятся к исследованию устойчивости «в малом», то есть в малой окрестности данного состояния равновесия, когда кривая мало отличается от прямой и соответственно отбрасываемые в формуле (2.3) слагаемые малы. Во-вторых, всё это относится только к описанному выше способу линеаризации уравнений – разложению нелинейных функций в степенные ряды, что геометрически соответствует замене кривой отрезком касательной, а не какому-либо другому способу линеаризации.

К сильно выраженным нелинейностям на больших участках, в том числе и к нелинейностям релейного типа, эти теоремы вообще неприменимы. Для исследования устойчивости нелинейных систем общего вида имеются другие методы, например, так называемый прямой метод Ляпунова.

Далеко не всегда бывает удобно вычислять корни характеристического уравнения. Поэтому желательно иметь такие методики, с помощью которых можно было судить об устойчивости системы непосредственно по коэффициентам характеристического уравнения без вычисления корней. Эти методики называются критериями устойчивости.