3. Уравнение третьего порядка

. (5.21)

Для этого уравнения имеем:

; (5.22)

. (5.23)

Последний определитель даёт условие а₃> 0. Условие Δ₂> 0, при а₀> 0, а₁> 0 и а₃> 0 может выполняться только при а₂> 0.

Следовательно, для уравнения третьего порядка уже недостаточно положительности всех коэффициентов характеристического уравнения. Требуется ещё выполнение определенного соотношения между коэффициентами а₁а₂> а₀а₃.

4. Уравнение четвертого порядка

. (5.24)

Подобно проделанному выше можно получить, что для уравнения четвёртого порядка кроме положительности всех коэффициентов требуется выполнение условия

. (5.25)

Существенным недостатком алгебраических критериев и, в том числе критериев Гурвица, является также то, что для уравнений высоких порядков в лучшем случае можно получить ответ о том, устойчива или не устойчива система автоматического регулирования. При этом в случае неустойчивой системы критерий не дает ответа на то, каким образом надо изменить параметры системы, чтобы сделать её устойчивой. Это обстоятельство привело к поискам других критериев, которые были бы более удобными в инженерной практике.

5.3. Критерий устойчивости Михайлова

Рассмотрим отдельно левую часть характеристического уравнения (5.7), которая представляет собой характеристический полином

. (5.26)

Подставим в этот полином чисто мнимое значение p = j, гдепредставляет собой угловую частоту колебаний, соответствующих чисто мнимому корню характеристического решения. В этом случае получим характеристический комплекс

, (5.27)

где вещественная часть будет содержать четные степени частоты

, (5.28)

а мнимая – нечетные степени частоты

. (5.29)

Е

Рис. 5.4. Годограф Михайлова

сли заданы все коэффициенты и определенное значение частоты, то величина D(j) изобразится на комплексной плоскости в виде точки с координатами U и V или в виде вектора, соединяющего эту точку с началом координат. Если же значение частотыменять непрерывно от нуля до бесконечности, то вектор будет изменяться по величине и направлению, описывая своим концом некоторую кривую (годограф), которая называетсякривой Михайлова(рис. 5.4).

Практически кривая Михайлова строится по точкам, причем задаются различные значения частоты и по формулам (5.28), (5.29) вычисляются U() и V(). Результаты расчетов сводятся в табл. 5.1.

Таблица 5.1

Построение кривой Михайлова

	0	…	∞
U	an	…	∞
V	0	…	∞

По этой таблице строится сама кривая (рис. 5.4).

Определим, чему должен равняться угол поворота вектора D(j) при изменении частотыот нуля до бесконечности. Для этого запишем характеристический полином в виде произведения сомножителей

, (5.30)

где ₁–_n– корни характеристического уравнения.

Характеристический вектор можно тогда представить в следующем виде:

. (5.31)

Каждая из скобок представляет собой комплексное число. Следовательно, D(j) представляет собой произведениеnкомплексных чисел. При перемножении аргументы комплексных чисел складываются. Поэтому результирующий угол поворота вектораD(j) будет равен сумме углов поворота отдельных сомножителей (5.31) при изменении частотыот нуля до бесконечности

. (5.32)

Определим каждое слагаемое в (5.31) по отдельности. Для обобщения задачи рассмотрим различные виды корней.

1. Пусть какой-либо корень, например ₁, являетсявещественным и отрицательным, то есть₁= –₁. Сомножитель в выражении (5.31), определяемый этим корнем, будет иметь вид (₁+ j). Построим годограф этого вектора на комплексной плоскости при изменении частотыот нуля до бесконечности (рис. 5.5,а). При= 0 вещественная частьU=₁, а мнимаяV= 0. Этому соответствует точка А, лежащая на вещественной оси. При0 вектор будет так изменяться, что его вещественная часть будет по-прежнему равна, а мнимая V =(точка В на графике). При увеличении частоты до бесконечности вектор уходит в бесконечность, причем конец вектора все время остается на вертикальной прямой, проходящей через точку А, а вектор поворачивается против часовой стрелки.

Рис. 5.5. Вещественные корни

Результирующий угол поворота вектора ₁ = +( / 2).

2. Пусть теперь корень ₁являетсявещественным и положительным, то есть₁= +₁.Тогда сомножитель в (5.31), определяемый этим корнем будет иметь вид (–₁+ j). Аналогичные построения (рис. 5.5, б) показывают, что результирующий угол поворота будет₁ = –( / 2). Знак минус показывает, что вектор поворачивается по часовой стрелке.

3. Пусть два сопряженных корня, например ₂и₃, являютсякомплексными с отрицательной вещественной частью, то есть_2;3= –±j. Аналогично сомножители в выражении (5.31), определяемые этими корнями, будут иметь вид (–j + j)( + j + j).

При = 0 начальные положения двух векторов определяются точками А₁ и А₂(рис. 5.6,а). Первый вектор повернут относительно вещественной оси по часовой стрелке на угол, равныйarctg( / ), а второй вектор – на тот же угол против часовой стрелки. При постепенном увеличенииот нуля до бесконечности концы обоих векторов уходят вверх в бесконечность и оба вектора в пределе сливаются с мнимой осью.

Результирующий угол поворота первого вектора ₂ = ( / 2) + . Результирующий угол поворота второго вектора₃ = ( / 2) –. Вектор, соответствующий произведению (–j + j)( + j + j) повернется на угол₂ + ₃= 2 / 2 =.

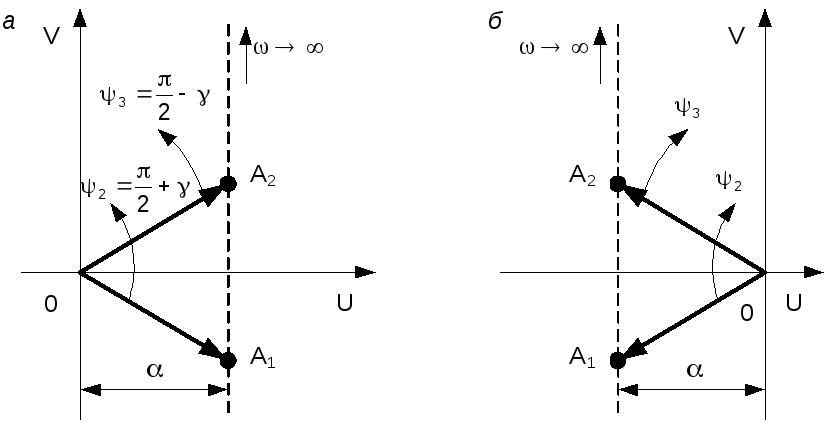
Рис. 5.6. Комплексные корни

4. Пусть те же комплексные корни имеют положительную вещественную часть, то есть_2;3= +±j.

Проводя построение аналогично рассмотренному ранее случаю (рис 5.6, б), получим результирующий угол поворота₂ + ₃= –2 / 2 = –.

Таким образом, если характеристическое уравнение будет иметь fкорней с положительной вещественной частью, то, каковы бы ни были эти корни (вещественные или комплексные), им будет соответствовать сумма углов поворотов, равная –f( / 2). Всем же остальным (n – f) корням характеристического уравнения, имеющим отрицательные вещественные части, будет соответствовать сумма углов поворотов, равная +(n – f)( / 2). В результате общий угол поворота вектора D(j) при изменении частотыот нуля до бесконечности по формуле (5.32) будет иметь вид

 = (n – f)( / 2) –f( / 2) = n ( / 2) –f . (5.33)

Этим выражением и определяется искомая связь между формой кривой Михайлова и знаками вещественных частей корней характеристического уравнения. В 1936 г. А.В. Михайловым был сформулирован следующий критерий устойчивости для линейных систем любого порядка.

Для устойчивости системы n-го порядка необходимо и достаточно, чтобы вектор D(j), описывающий кривую Михайлова, при изменении  от нуля до бесконечности имел угол поворота  =n ( / 2).

Эта формулировка непосредственно вытекает из (5.33). Для устойчивости системы необходимо, чтобы все корни лежали в левой полуплоскости.Отсюда определяется требуемый результирующий угол поворота вектора.

Критерий устойчивости Михайлова формулируется следующим образом: для устойчивости линейной САР необходимо и достаточно, чтобы годограф Михайлова при изменении частоты от нуля до бесконечности, начавшись на положительной полуплоскости и не пересекая начала координат, последовательно пересек столько квадрантов комплексной плоскости, какой порядок имеет полином характеристического уравнения системы.

О

Рис. 5.7. Устойчивые САР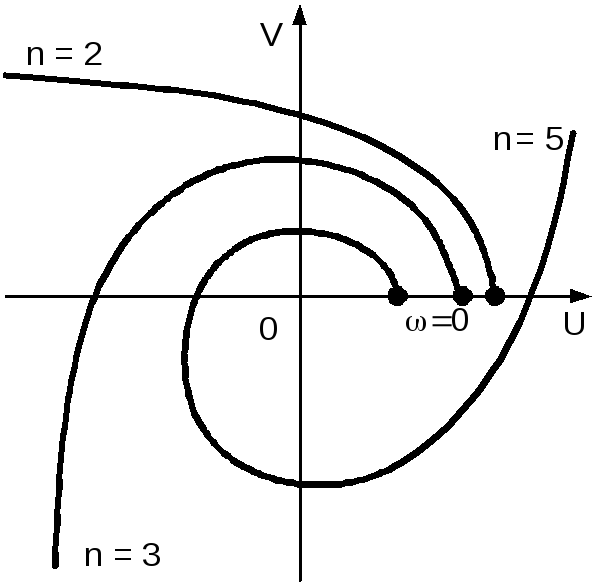

казывается, что кривая Михайлова для устойчивых систем всегда имеет плавную спиральную форму, причем конец ее уходит в бесконечность в том квадранте комплексной плоскости, номер которого равен степени характеристического уравнения (рис. 5.7). Больше чемnчисло квадрантов кривая Михайлова вообще не может пройти. Поэтому неустойчивость системы всегда связана с тем, что в кривой Михайлова нарушается последовательность прохождения квадрантов, вследствие чего угол поворота вектораD(j) оказывается меньше, чемn ( / 2) (рис. 5.8).

Для устойчивой системы кривая Михайлова проходит последовательно nквадрантов комплексной плоскости.

Наличие границы устойчивости всех трех типов может быть определено по кривой Михайлова следующим образом.

При наличии границы устойчивости первого типа(нулевой корень) отсутствует свободный член характеристического полиномаa_n= 0, и кривая Михайлова выходит из начала координат (рис. 5.9, кривая 1)

Рис. 5.8. Неустойчивая САР

Рис. 5.9. Границы устойчивости

При границе устойчивости второго типа(колебательная граница устойчивости) левая часть характеристического уравнения, то есть характеристический полином, обращается в нуль при подстановке p = j₀

D(j₀) = X(₀) + Y(₀) = 0. (5.34)

Откуда вытекают два равенства: X(₀) = 0;  Y(₀) = 0. Это значит, что точка  = ₀ на кривой Михайлова попадает в начало координат (рис. 5.9, кривая 2). При этом величина ₀ есть частота незатухающих колебаний системы.

Для границы устойчивости третьего типа(бесконечный корень) конец кривой Михайлова перебрасывается (рис. 5.9, кривая 3) из одного квадранта в другой через бесконечность. При этом коэффициент а₀характеристического полинома (5.7) будет проходить через нулевое значение, меняя знак с плюса на минус.