5.3. Планирование эксперимента для применения регрессионного анализа

5.3.1. Некоторые общие положения регрессионного анализа

Регрессионный анализ (РА) - метод математической статистики, который позволяет выявить приближенную количественную зависимость (f) свойства объекта yот значений факторовx_j, оказывающих влияние на это свойство. Эта приближенная зависимость, выраженная в виде конкретной математической функции, называется уравнением регрессии:

.

Проводить РА можно только для количественных значений y и x_j.

При РА решают две основные задачи:

1. Ищут с помощью метода приближения уравнение регрессии, наиболее точно описывающее истинную зависимость y = (x_j)по результатам измерения свойств объекта при различных значениях факторов:

y = (x₁, x₂, ..., x_j, ...x_k )+= f(x₁, x₂, ..., x_j, ...x_k )+ + .

2. Оценивают ошибки (+), допускаемые при описании истинной зависимостис помощью найденного уравнения регрессии.

Порядок проведения РА (его тип) зависит от плана эксперимента. Различают классический РА (КРА) и РА при математическом планировании эксперимента (РАМПЭ).

5.3.2. Составление планов эксперимента для проведения регрессионного анализа

5.3.2.1. Составление планов эксперимента для проведения классического регрессионного анализа

Общим требованием к планированию любого эксперимента для проведения КРА является выполнение условия m_j > 2.Другие рекомендации аналогичны планированию эксперимента для проведения дисперсионного анализа.

После планирования и завершения эксперимента проведение КРА его результатов проводят в такой последовательности:

1. Выбираютсемейство математических функций, в котором предполагается найти уравнение регрессии (семейство прямых, парабол, гипербол и др.).

2. Выбираютметод приближения.

3. Для выбранного семейства функций с помощью метода приближения рассчитывают параметры функции (коэффициенты уравнения регрессии).

4. Проверяют рассчитанные коэффициенты уравнения регрессии на значимость (равенство нулю).

5. Корректируют вид исходной функции, исключая из нее незначимые коэффициенты и другие составляющие.

6. Рассчитывают параметры скорректированной функции (скоррек­тированные коэффициенты уравнения регрессии) и возвращаются к выполнению пунктов 4,5. Пункт 6 выполняют до тех пор, пока в уравнении регрессии останутся только значимые коэффициенты (значения коэффициентов могут изменяться после каждого пересчета)

7. Оценивают ошибки ( + ), допускаемые при описании истинной зависимостис помощью найденного уравнения регрессии: проверяют адекватность уравнения регрессии с помощью закона распределения Фишера или рассчитывают вероятность описания зависимостифункциейf.

8. Выбираютдругое семейство математических функций и (или) метод приближения и с ними последовательно выполняют пункты 3-7.

9. Из группы найденных уравнений регрессии в ряду разных семейств функций выбираютокончательное уравнение регрессии по следующим соображениям:

а) вид данного уравнения регрессии совпадает с теоретическими законами поведения объекта;

б) данное уравнение регрессии описывает поведение объекта с наибольшей вероятностью;

в) при одной вероятности для данного уравнения регрессии наблюдается наибольшее значение соотношения факторной и остаточной дисперсий (F-соотношения).

При выборе семейства функций (пункты 1 и 8), если нет сведений или теоретических предположений о типе зависимости , обычно действуют по принципу "от простого к сложному". При этом начинают с семейства прямых ("линейная регрессия") или трансцендентных функций, которые легко преобразуются в линейную форму ("трансцендентная регрессия").

При неадекватности найденного линейного уравнения регрессии или неудовлетворенности его точностью можно переходить к семейству полиномов с постепенным увеличением их степени (полиномы второго, третьего и др. порядков) до тех пор, пока не начнет уменьшаться F-соот­ношение. Вид функции также зависит от числа одновременно изменяемых факторов при эксперименте.

Наиболее часто при выполнении РА в качестве метода приближения используют метод наименьших квадратов (МНК). Однако применение МНК является корректным при выполнении следующих требований:

а) единичные результаты измерения свойств y должны быть независимыми случайными величинами;

б) выборочные дисперсии y_zдолжны быть однородными (одинаковыми).

При невыполнении этих условий используют другие методы приближения (непараметрические методы регрессии).

Алгоритмы всех необходимых при КРА расчетов (пункты 3,4,6,7) зависят от выбранного семейства функций, метода приближения, наличия повторных опытов, количества исследуемых факторов (изучить самостоятельно [6,7,8,11]).Многие из этих алгоритмов реализованы в статистических программных продуктах, математических пакетах (MathCAD и др.), электронных таблицах (Excel и др.).

Следует отметить, что выполнение пункта 9 носит субъективный характер и для него пока еще нет общепризнанных рекомендаций.

Пример проведения классического регрессионного анализа.Воспользуемся для примера данными эксперимента, приведенными в табл. 7.

По полю корреляции (см. рис. 4) можно предположить линейный характер зависимости y от х, поэтому начнем проведение КРА с выбора семейства прямых и представления искомого уравнения регрессии в виде

= а +bx.

Так как в этом эксперименте не проводились повторные опыты, то невозможно оценить однородность дисперсий при различных уровнях фактора хи установить закон распределенияy.Поэтому делаем допущение о нормальном законе распределенияyи равенстве дисперсий (одинаковой случайной ошибке при любом значении х). Тогда в качестве метода приближения можно взять МНК.

Используя метод МНК и учитывая отсутствие повторных опытов, выполним расчеты коэффициентов уравнения регрессии а и b[1]:

b = 1,3 (мас. %/мин);a = y - bx = 42,5 - 1,3115;

а = - 107 (мас. %).

Так как дисперсия воспроизводимости эксперимента неизвестна и ее невозможно определить (из-за отсутствия повторных опытов), то проверку коэффициентов а иbна значимость не проводим. Делаем допущение, что эти коэффициенты "значимы", т.е. не равны нулю.

Найденное линейное уравнение регрессии имеет следующий вид:

= - 107 + 1,3х.

Для оценки ошибки, допускаемой при описании истинной зависимости с помощью найденного уравнения регрессии при отсутствии повторных опытов и дисперсии воспроизводимости, составимF-соотно­шение(F_p) между дисперсией относительноy() и остаточной дисперсией () в соответствии со следующими формулами:

; ; ,

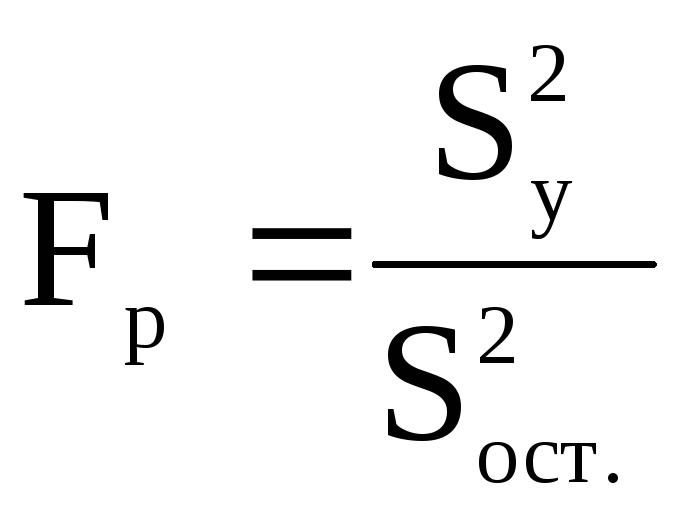где L -число значимых коэффициентов в скорректированном уравнении регрессии (L = 2).

Выполним необходимые расчеты:

,

 290 (мас. %)²;

,

15 (мас. %)²;

;

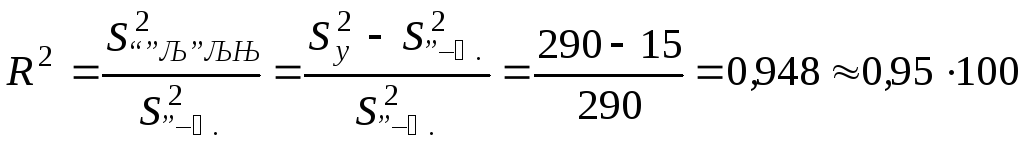% = 95 %;

(гдеR -выборочный корреляционный коэффициент Пирсона,R² - коэффициент детерминации).

Найденное линейное уравнение регрессии (= - 107 + 1,3х) с вероятностью, большей 0,95,адекватноописывает реальную зависимость выхода нитробензола от времени его синтеза, так как значение соотношенияF_p больше табличного значения квантиля распределения Фишера при=0,05 и степенях свободыf₁ = N-1 иf₂ = N-L (F_т= 19,2). Точность описания (коэффициент детерминацииR²) реальной зависимости найденным линейным уравнением регрессии составляет 95 %.

Подобные расчеты были выполнены на ПЭВМ с помощью статистического пакета STATGRAPHICS[7]не только для семейства прямых, но и некоторых других функций (табл. 15).

Данные табл. 15 показывают, что выход нитробензола зависит от времени его синтеза и эта зависимость с наибольшей вероятностью ( Р0,983) описывается линейным уравнением вида

= - 107 + 1,3х.

Оба коэффициента уравнения регрессии (а = - 107 и b= 1,3) с вероятностью Р>0,96 являются "значимыми" (т.е. не равными нулю), так как уровень их значимости равен соответственно_а = 0,033 и_b = 0,017.

Таблица 15

Результаты расчетов на ПЭВМ

Функ­ция	Коэф­фици­ент					F-	Адек-
	обо­з­на­­че­ние	значе­ние	S	tт		соот- но-ше- ни­	ват-­ но­сть ()
y = a + bx	a b	- 107 1,3	20,013 0,173	- 5,347 7,506	0,033 0,017	56,33	0,017
y = e^(a+b^x^)	a b	- 0,3741 0,03519	0,9969 0,0086	-0,375 4,078	0,744 0,055	25,88	0,055
1/y = a + bx	a b	0,14867 -0,00105	0,0423 0,0004	3,5128 -2,867	0,072 0,103	11,07	0,103

Более подробно с проведением классического регрессионного анализа для практических целей можно ознакомиться в [11].