2.4. Таблицы истинности сложных высказываний
Рассмотрим более сложные высказывания, или формулы алгебры логики, которые получаются из простейших высказываний.
Построение таблиц истинности для таких формул производится следующим образом. Вначале выписываются значения, которые могут принимать наборы переменных в этой формулы. В общем случае, если переменных n, то различных n-мерных наборов переменных существует 2n.
Затем вычисляется значение формулы на каждом наборе. Любая рассматриваемая логическая формула представляет собой суперпозицию (подстановку) элементарных высказываний и может быть вычислена последовательно, при помощи подстановок определенных ранее значений.
Задача 2.2. Построить таблицу истинности для формулы
F(x1, x2, x3) = (x1 → x2)→ x3 .
Решение. Определим значение наборов переменных. Их восемь
– 000, 001, 010, 011, 100, 101, 110, 111. Каждому из них можно по-
ставить в соответствие десятичный эквивалент (0, 1, …, 7). Построим таблицу истинности рассматриваемой функции. На
первом шаге выписываем значение наборов переменных:
x1 x2 x3
0 0 0
0 0 1
0 1 0
0 1 1
1 0 0
1 0 1
1 1 0
1 1 1
На втором шаге, определяем порядок выполнения элементарных высказываний и заполняем ими заголовки столбцов.
На третьем шаге вычисляем значение x1→ x2. На четвертом шаге вычисляем значение x3 .
53
На пятом шаге вычисляем значение (x1→ x2)→ x3 , зная значения x1→ x2 и x3 на каждом возможном наборе:
x1 x2 x3 |
x1→ x2 |
x3 |
(x1→ x2)→ x3 |
0 0 0 |
1 |
1 |
1 |
0 0 1 |
1 |
0 |
0 |
0 1 0 |
1 |
1 |
1 |
0 1 1 |
1 |
0 |
0 |
1 0 0 |
0 |
1 |
1 |
1 0 1 |
0 |
0 |
1 |
1 1 0 |
1 |
1 |
1 |
1 1 1 |
1 |
0 |
0 |
Таблица истинности построена.
Задача 2.3. Построить таблицу истинности для формулы: (a b)& c.
Решение. Таблица истинности будет выглядеть следующим образом:
a b c |
|
|
|
|
|
|
(a |
|
) & c |
|
b |
|
a |
b |
|
b |
|||
|
|
|
|
|
|
0 |
|
|
|
0 0 0 |
1 |
|
1 |
|
|
|
|
||
0 0 1 |
1 |
|
1 |
|
|
1 |
|
|
|
0 1 0 |
0 |
|
0 |
|
|
0 |
|
|
|
0 1 1 |
0 |
|
0 |
|
|
0 |
|
|
|
1 0 0 |
1 |
|
0 |
|
|
0 |
|
|
|
1 0 1 |
1 |
|
0 |
|
|
0 |
|
|
|
1 1 0 |
0 |
|
1 |
|
|
0 |
|
|
|
1 1 1 |
0 |
|
1 |
|
|
1 |
|
|
|
Задача 2.4. Построить таблицу истинности для формулы:
( a →b) →c .
Решение. Таблица истинности будет выглядеть следующим образом:
54
a b c |
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
→ b |
( |
a |
→b) |
( |
a |
→b) → c |
||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 0 0 |
0 |
|
|
1 |
|
|
|
0 |
|
|
|
|||
0 0 1 |
1 |
1 |
|
|
0 |
|
|
|
1 |
|
|
|
||
0 1 0 |
1 |
0 |
|
|
1 |
|
|
|
0 |
|
|
|
||
0 1 1 |
1 |
1 |
|
|
0 |
|
|
|
1 |
|
|
|
||
1 0 0 |
0 |
1 |
|
|
0 |
|
|
|
1 |
|
|
|
||
1 0 1 |
0 |
1 |
|
|
0 |
|
|
|
1 |
|
|
|
||
1 1 0 |
0 |
1 |
|
|
0 |
|
|
|
1 |
|
|
|
||
1 1 1 |
0 |
1 |
|
|
0 |
|
|
|
1 |
|
|
|
||
Две формулы A и B называются равносильными, если на одинаковых наборах переменных обе формулы принимают одинаковые значения (А=В).
Задача 2.5. Сравните следующие логические формулы и определите, являются ли они равносильными f1 = (x1 x2) x3 и f2 = (x1
→x2) → x3 .
Решение. Определим значение наборов переменных. Последова-
тельно вычислим значение первой операции (сложения по Жегалкину x1 и x2). Затем вычислим значение операции (x1 x2) x3. Построим таблицу истинности для f1:
x1 x2 x3 |
x1 x2 |
(x1 x2) x3 |
0 0 0 |
0 |
0 |
0 0 1 |
0 |
0 |
0 1 0 |
1 |
0 |
0 1 1 |
1 |
1 |
1 0 0 |
1 |
0 |
1 0 1 |
1 |
1 |
1 1 0 |
0 |
0 |
1 1 1 |
0 |
0 |
Теперь надо сравнить полученные значения со значениями функции f2 на этих же наборах переменных. Построим таблицу истинности для f2:
55
x1 x2 x3 |
x1 x2 |
|
x3 |
|
(x1 x2) |
x3 |
|
0 0 0 |
1 |
1 |
|
1 |
|
|
|
0 0 1 |
1 |
0 |
|
0 |
|
|
|
0 1 0 |
1 |
1 |
|
1 |
|
|
|
0 1 1 |
1 |
0 |
|
0 |
|
|
|
1 0 0 |
0 |
1 |
|
1 |
|
|
|
1 0 1 |
0 |
0 |
|
1 |
|
|
|
1 1 0 |
1 |
1 |
|
1 |
|
|
|
1 1 1 |
1 |
0 |
|
0 |
|
|
|
Функции f1 и f2 не являются равносильными, так как их значения различны на наборах 0, 2, 3, 4 и 6.
2.5. Равносильности алгебры высказываний
Важнейшие равносильности алгебры высказываний можно разбить на три группы:
основные равносильности;
равносильности, выражающие одни операции через другие;
равносильности, выражающие основные законы алгебры высказываний.
Основные равносильности:
x&x = x |
x x=x |
||||
x&1= x |
x 1=1 |
||||
x&0 = 0 |
x 0= x |
||||
x& |
|
|
=0 |
|
|
x |
|
||||
x |
|
= 1 |
|
||
x |
|
||||
x=x
x& (x y) = x, x (x & y) = x
–законы идемпотентности;
–законы работы с 0 и 1;
–закон противоречия;
–закон исключения третьего;
–закон снятия двойного отрицания;
–законы поглощения.
Равносильности, выражающие одни операции через другие: x y= (x y)&(y x);
56
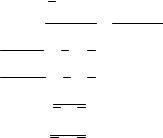
x y = x y;
x y =(x y) (y x);
(x y) x & y ;
(x & y) x y ;
x& y x y;
x y x& y.
Равносильности, выражающие основные законы алгебры вы-
сказываний:
x & y= y & x
x y = y x
(x & y) & z = x & (y & z) (x y) z = x (y z) x &(y z)= x & y x & z
x (y & z)= (x y) & (x z)
–коммутативность конъюнкции;
–коммутативность дизъюнкции;
–ассоциативность конъюнкции;
–ассоциативность дизъюнкции;
–дистрибутивность конъюнкции относительно дизъюнкции;
–дистрибутивность дизъюнкции относительно конъюнкции.
Используя равносильности всех трех групп, можно часть формулы заменить равносильной ей формулой. Такие преобразования называются равносильными.
Операции дизъюнкция, конъюнкция, отрицание, импликация и эквивалентность составляют сигнатуру алгебры высказываний [1]:
А = < {0,1}, &, , ¯, , >.
Рассмотрим непустое множество М элементов любой природы {x, y, z,…}, которые могут быть в том числе и высказываниями. На множестве М определено отношение = «равно» и три операции: + («логическое сложение»), ∙ («логическое умножение»), ¯ («отрицание»), подчиняющиеся законам коммутативности, ассоциативности, дистрибутивности, идемпотентности, двойного отрицания, де Моргана, поглощения.
57