Приведенная задача демонстрирует необходимость дополнительной проверки: следует убедиться, что информация дана про все вершины или обозначить как неизвестные переменные степени остальных вершин и решать задачу уже исходя из этого. Уменьшенная ровно в 2 раза суммарная степень однозначно определяет количество ребер в графе.
Итак, первое условие – четность суммарной степени вершин графа. Далее можно попробовать проверить выполнение ограничений на минимальное и максимальное число ребер в графе.
6.10.3. Оценка количества ребер сверху и снизу
Оценка количества ребер сверху и снизу проводится на основе нескольких фактов.
1.Степень каждой вершины полного графа на единицу меньше числа его вершин, полный граф на n вершинах всегда является регулярным графом степени (n – 1), суммарная степень его вершин равна n(n + 1), а значит, количество ребер в полном графе равно n(n+1)/2. Это и есть ограничение количества ребер сверху – построить больше на n вершинах нельзя. Например, у графа на 7 вершинах максимально может быть 21 ребро.
2.Максимальное число ребер на n вершинах можно построить именно в случае, когда граф связный. Иначе их будет еще меньше, например, у несвязного графа на n вершинах в лучшем случае количество ребер равно (n–1)·(n – 2)/2 (лучший случай попытки разместить максимальное число ребер – это отделить одну изолированную вершину и построить полный граф на оставшихся (n – 1) вершине). Например, у несвязного графа на 7 вершинах максимально может быть 15 ребер.
3.Оценка снизу чаще всего сводится к оценке количества ребер, необходимых для образования именно связного графа. Минимальная с точки зрения расхода ребер конфигурация состоит именно в построении дерева. В дереве на n вершинах содержится всегда
(n – 1) ребро.
4.Если помимо условия ацикличности поставлено также требование обеспечить несвязность графа, то ребер удастся разместить
216
еще меньше. Их будет столько же, сколько ребер в остовном лесе: на n вершинах при k компонентах связности ациклический граф содержит в общем случае (n – k) ребер.
5. Если речь идет о двудольных графах, полезно помнить, что число ребер в полном двудольном графе с n1 и n2 вершинами в соответствующих долях равно n1·n2
В ряде случаев эти факты позволяют либо доказать невозможность построения графа с заданными характеристиками, либо помогают сформировать представление о свойствах графа.
Задача 6.20. Построить или обосновать невозможность построения несвязного графа на 12 вершинах, имеющего 56 ребер.
Решение. Несвязный граф состоит минимум из двух компонент, при этом наиболее экономичный в плане потенциально наибольшего количества ребер способ распределения вершин это 1 вершина в первой компоненте и остальные 11 – во второй. На 11 вершинах можно построить максимально 11·10/2=55 ребер, таким образом ,получим полный граф на 11 вершинах. Следовательно, графа, соответствующего условию задачи, не существует.
Задача 6.21. Построить или обосновать невозможность построения связного графа на 11 вершинах, имеющего следующее распределение степеней вершин: две вершины степени 3, три вершины степени 2, шесть вершин степени 1.
Решение. Суммарная степень всех вершин равна 2·3+3·2+6·1=18, следовательно, в графе должно быть 18/2=9 ребер. Однако для построения связного графа на 11 вершинах необходимо как минимум 10 ребер. Следовательно, графа, соответствующего условию задачи, не существует.
Задача 6.22. Построить или обосновать невозможность построения бихроматического графа на 13 вершинах, имеющего 41 ребро.
Решение. Бихроматическими являются двудольные графы, значит, имеющиеся 13 вершин нужно распределить на 2 доли так, чтобы удалось провести максимальное количество ребер. Самое выгодное разбиение – это соотношение по 50%, в данном случае это 6 и 7 вершин соответственно. При таком разбиении можно максимально построить 6·7=42 ребра. Нам нужно 41, значит, ответом яв-
217
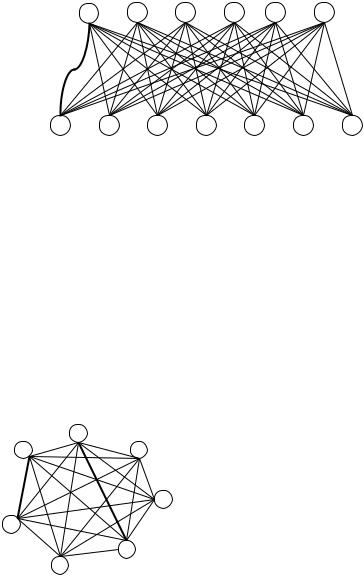
ляется полный граф K6,7, у которого удалили одно ребро. Граф, являющийся ответом на задачу 6.22, представлен на рис. 6.62.
Рис. 6.62
6.10.4. Получение недостающих данных на основе формул
Вряде задач на построение дополнительную информацию о структуре графа можно получить на основе численных характеристик, таких, как цикломатическое число, ранг, хроматическое число графа, числа внешней и внутренней устойчивости и другие характеристики. Во всех этих случаях из приведенных в условии задачи данных желательно извлечь дополнительные сведения, которые могут помочь в непосредственном построении графа.
Вкачестве примера приведем несколько типовых задач.
Задача 6.23. Построить или обосновать невозможность построения связного графа на 7 вершинах, цикломатическое число
|
которого равно 13. |
|
Решение. В силу того, что граф |
|
связный, k = 1, по условию n = 1. Из |
|
формулы (5.1) получим: 13 = m – 7 + 1, |
|
откуда m = 19. В графе на 7 вершинах |
|
максимально можно построить 7·6/2 = |
|
= 21 ребро. Значит, искомый граф |
|
представляет собой полный граф на 7 |
|
вершинах, в котором удалено два реб- |
Рис. 6.63 |
ра. Граф, являющийся ответом на за- |
дачу 6.23, представлен на рис. 6.63. |
218
Задача 6.24. Построить или обосновать невозможность построения бихроматического связного графа, у которого ранг равен 12, а цикломатическое число равно 28.
Решение. Согласно формулам вычисления цикломатического числа и ранга получим:
χ(G) = n – k =12;
γ(G)= m – n + k = m –(n – k) = 28.
Решив систему уравнений, получим 28 = m–12, откуда m = 40. Поскольку граф связный, k = 1 и, значит, n = 13. Бихроматическими являются двудольные графы, значит, нужно разбить множество из 13 вершин на два подмножества так, чтобы удалось построить нужное количество ребер. Наиболее рациональный способ такого разбиения – пополам, что в данном случае соответствует 6 и 7 вершинам в каждой доле двудольного графа. При этом максимальное число ребер в полном двудольном графе K6,7 равно 6·7 = 42, а значит 40 ребер можно построить на данном количестве вершин. Граф, являющийся ответом на задачу 6.24, представлен на рис. 6.64.
Рис. 6.64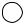 
Задача 6.25. Построить или обосновать невозможность построения двухкомпонентного графа на 18 вершинах, имеющего 15 ребер.
Решение. Исходя из условия задачи k = 2, n = 18, m = 15. Применим формулу нахождения цкломатического числа:
γ(G)= m – n + k =15 – 18 + 2 = –1.
Однако цикломатическое число не может быть отрицательным. Следовательно, графа, соответствующего условию задачи, не существует.
219