Загребаев Методы обработки статистической информации в задачах контроля 2008

Свойства математического ожидания

1. Математическое ожидание постоянной неслучайной величины равно самой этой величине:

M [c]= c .

(1.1.17)

2. Математическое ожидание от произведения постоянной величины с на случайную величину X равно произведению постоянной на математическое ожидание случайной величины:

M [cX ]= cM [X ].

(1.1.18)

Модой дискретной случайной величины X называется ее наиболее вероятное значение – μ.

Модой непрерывной случайной величины X называется то её значение, при котором плотность вероятности максимальна – обо-

значается также – μ. Для непрерывной случайной величины нельзя говорить о наиболее вероятном значении, так как вероятность любого конкретного значения одинакова и равна нулю.

Медианой случайной величины X называется такое её значение,

для которого выполняется равенство								P(X > μe ) = P(X < μe ) , где
μe – медиана,				т.е. есть прямая x = μe				делит площадь под кривой
функции f (x)				на две равные части.

μe m μ

Рис. 1.4. Геометрическая иллюстрация числовых характеристик

21

Если многоугольник (плотность) распределения имеют один максимум, то такое распределение называется унимодальным, более одного – полимодальным. Если имеет один минимум, то антимодальным. Геометрический смысл числовых характеристик показан на рис. 1.4 для непрерывной случайной величины.

Моменты случайной величины

Начальным моментом k-го порядка дискретной случайной величины называется сумма

n
αk [X ]= ∑xik pi .	(1.1.19)

i=1

Начальным моментом k-го порядка непрерывной случайной величины называется интеграл

αk [X ]= +∞∫ xik f (x)dx .	(1.1.20)
−∞

Здесь возможные значения случайной величины возводятся в степень k.

Таким образом, введенная ранее величина – математическое ожидание – есть не что иное, как первый ( k =1) начальный момент случайной величины X.

Обобщая формулы (1.1.19) и (1.1.20), можно записать:

	k	(1.1.21)
αk [X ]= M X	.

Центрированной случайной величиной называется случайная величина, представляющая собой отклонение от математического

ожидания X = X − mx = X − M [X ].

Центрирование случайной величины означает перенос начала отсчета в точку с координатой, равной математическому ожиданию. Действительно, очевидны следующие соотношения как для дискретной, так и для непрерывной случайной величины:

	n	n	n	n
M X	=∑(xi −mx)pi =∑xi pi −∑mx pi =mx −mx∑pi =mx −mx =0;
	i=1	i=1	i=1	i=1

22

		+∞	+∞	+∞
		= ∫ (x −mx )f (x)dx = ∫ xf (x)dx −mx ∫ f (x)dx =mx −mx =0.
	M X
		−∞	−∞	−∞

Моменты центрированной случайной величины носят название центральных моментов. Центральный момент k-го порядка по определению есть:

μ	k	= M ( X − m)k		= M ( X )k .		(1.1.22)
Для дискретной случайной величины в явном виде
			n
		μk	= ∑(xi − m)k pi .			(1.1.23)
			i=1
Для непрерывной случайной величины в явном виде
			+∞
		μk = ∫ (x − mx )k f (x)dx .				(1.1.24)

−∞

Наиболее важной характеристикой, наряду с математическим ожиданием, является второй центральный момент μ2 , называемый дисперсией. Введем для этой величины специальное обозначение Dx или, понимая под символом D операцию нахождения диспер-

сии, D[X ]. В явном виде эта величина имеет следующие выраже-

ния:

для дискретной случайной величины

n	− m)2 pi ;
D[X ]= Dx = μ2 = ∑(xi		(1.1.25)
i=1
для непрерывной случайной величины
+∞
D[X ]= Dx = μ2 = ∫ (x − mx )2 f (x)dx .		(1.1.26)

−∞

Дисперсия есть мера рассеянности, разбросанности случайной величины около ее математического ожидания.

Между центральными и начальными моментами существует однозначная связь. Например, для момента второго порядка – дисперсии – получим:

23

Dx = M [( X − mx )]= M

2

2

=

X

− 2 Xmx + mx

= M X 2

− 2m

m

x

+ m2

= α

2

− m2 .

(1.1.27)

x

x

x

Дисперсия имеет размерность квадрата соответствующей случайной величины. Для наглядной характеристики рассеивания удобнее пользоваться величиной, размерность которой совпадает с размерностью случайной величины. Для этого из дисперсии извлекают квадратный корень. Полученная величина называет средним

квадратическим отклонением случайной величины: σx = Dx . На

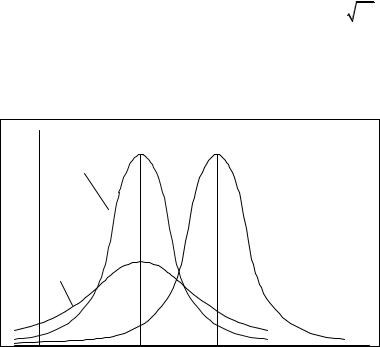
рис. 1.5 показан пример вида функции плотности распределения двух случайных величин, имеющих одно и то же математическое ожидание, но разные дисперсии и имеющих одну и ту же дисперсию, но различные математические ожидания.

D2	D1 > D2
	m2 > m1
D1
m1	m2
Рис. 1.5. Графическая иллюстрация моментов случайной величины

24

Законы распределения случайной величины

Закон равномерной плотности

Если известно, что значение случайной величины находится в пределах некоторого интервала, а плотность вероятности распределения в пределах этого интервала постоянна, то говорят, что случайная величина подчинена закону равномерной плотности.

Закон равномерной плотности или равномерный закон распределения непрерывной случайной величины имеет функцию плотности распределения вида

0,

x ≤ α;

α < x ≤ β;

(1.1.28)

f (x) = c,

x >β.

0,

+∞

β

1

Из условия ∫

f (x)dx = ∫ f (x)dx =1 следует, что

c =

. На

β − α

−∞

α

рис. 1.6 показана функция плотности распределения f (x) ,

а на

рис. 1.7 – функция распределения

F (x) для закона равномерной

плотности.

f (x)

c

P(α < X < β)

α

a

b β

Рис. 1.6. Функция плотности распределения в законе равномерной плотности

25

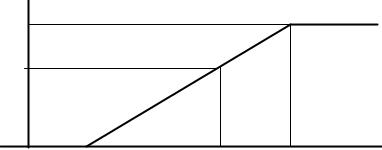
F (x)
1
	P(α < X < x)
α	x	β	X
Рис. 1.7. Функция распределения в законе равномерной плотности

Используя связь между плотностью распределения и функцией распределения, получим

x

x

F(x) = ∫ f (x)dx = ∫ f (x)dx .

Тогда

−∞

α

x

x − α

∫ f (x)dx =

,

α < x ≤ β;

β − α

F(x) =

α

(1.1.29)

β

1

∫

dx =1,

x > β.

β − α

α

Числовые характеристики

равномерно распределенной случайной величины

Математическое ожидание

+∞

β

1

dx = β+ α .

mx = ∫

xf (x)dx = ∫ x

(1.1.30)

β −α

−∞

α

2

Дисперсия

+∞

Dx = ∫ (x − mx )2 f (x)dx =

−∞

β

β+ α 2

1

(β − α)2

.

(1.1.31)

= ∫ x

−

dx =

2

β − α

12

α

26

В силу симметрии медиана совпадает с математическим ожида-
нием, а так как функция плотности распределения не имеет макси-
мума, то мода отсутствует.
Для получения вероятности попадания случайной величины в
интервал (a, b) можно воспользоваться явным видом функции рас-
пределения (1.29):
		P(a < X < b) = F(b) − F(a) = b − a .										(1.1.32)
										β − α
Из выражения (1.1.32) видно, что вероятность попадания в интер-
вал (a, b) равна отношению длины интервала ко всей длине участка
(α, β) и не зависит от его месторасположения на этом участке.
				Закон Пуассона
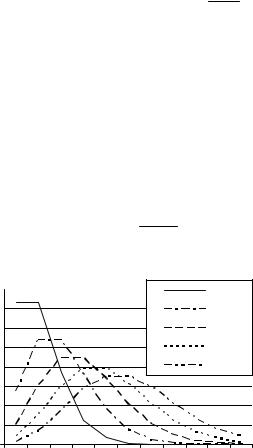
Частным случаем биномиального распределения является закон
Пуассона (рис. 18). Можно показать, что если в биномиальном за-
коне число испытаний увеличивать ( n →∞ ), а вероятность собы-
тия при этом уменьшать ( p → 0 ), но так, чтобы np = a , то биноми-
альный закон превращается в закон Пуассона:
					P(m) =		a ml−a					(1.1.33)
							m!	.
	0,4									np=1
	0,35									np=2
	0,3									np=3
вероятность	0,25									np=4
	0,2									np=5
	0,15
	0,1
	0,05
	0
	1	2	3	4	5	6	7	8	9	10	11
					число событий

Рис. 1.8. Закон Пуассона

27

Параметр a в законе Пуассона есть математическое ожидание числа появлений редких (т.е. вероятность каждого отдельного события мала), но массовых (т.е. опытов может быть много) случайных событий. Оказывается, что дисперсия случайной величины тоже равна a:

∞	∞		a	m	−a
D = ∑	(m − λ)2 P(m) = ∑	(m − a)2		l		= a . (1.1.34)
				m!
m=0	m=0

Показательный закон распределения

Показательным называется закон распределения случайной величины, в данном случае обозначим ее T, имеющий плотность вероятности вида:

	−λ t	, t ≥ 0;
λe			(1.1.35)
f (t) =	t < 0.
0,

Показательным распределением описывается довольно большой круг задач, начиная от задач надежности до задач ядерной физики.

	+∞	+∞			1
	M [T ]= mt = ∫ t f (t)dt = ∫ t λ l−λ t dt =					.	(1.1.36)
	−∞	0			λ
	Легко показать, что дисперсия случайной величины T есть
	D[T ]= ∞∫	(t − mt )2 f (t)dt =	1	.			(1.1.37)
	0		λ2

Геометрическая интерпретация показательного закона распределения приведена на рис. 1.9.

Нормальный (гауссов) закон распределения случайных величин играет особую роль. Во-первых, это наиболее часто встречающийся на практике закон распределения. Это обстоятельство объясняется тем, что большинство случайных величин представляют собой сумму большого числа независимых случайных величин, влияние каждой из которых мало. Предельные теоремы теории вероятностей, о которых мы будем говорить ниже, доказывают, что вне зависимости от того, по какому закону распределено каждое из слагаемых, закон распределения суммы будет близок к нормальному.

28

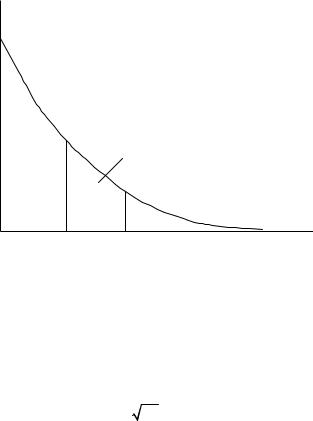
Это приводит, например, к тому, что ошибки измерения подчиня-
ются нормальному закону
f (t)
	P(t1 < T < t2 )
t1	t2
Рис. 1.9. Плотность распределения в показательном законе

Нормальный закон распределения

Нормальный закон распределения характеризуется функцией плотности распределения вида:

	1		−(x−mx )2
f (x) =		e		2σ2x	.	(1.1.38)
	σx 2π

Можно показать, что mx есть ни что иное, как математическое ожидание, а σx – среднее квадратическое отклонение случайной

величины X.

Поведение плотности распределения в зависимости от параметров mx и σx показано на рис. 1.10.

Изменение математического ожидания приводит к сдвигу максимума функции, а изменение дисперсии к ее «уширению» либо «сужению», соответственно, при росте или уменьшении σ.

29

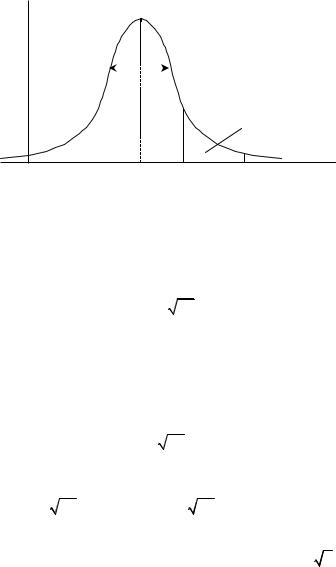
f (x)
σx
		P(α < X <β)
mx	α	β	x
Рис. 1.10. Плотность распределения в нормальном законе

Функция распределения случайной величины X, распределенной по нормальному закону, есть

x		1		x	−	(x−mx )
						2σ2
F(x) = ∫	f (x)dx =			∫ l			dx .	(1.1.39)
						x
		σx
−∞			2π −∞

Найдем вероятность попадания случайной величины X на участок от α до β. Согласно формуле:

P(α < X < β) = F (β) − F (α) ;

1

β

−(x−mx )

F(α) − F(β) =

∫ l

2σ2x

dx −

σx

2π

−∞

1

α

−(x−mx )

1

β

−(x−mx )

−

∫ l

2σ2x

dx =

∫l

2σ2x

dx .

(1.1.40)

σx

σx

2π −∞

2π α

После замены переменных в выражении (1.1.40)

t =

x − mx

лег-

σx

2

ко показать, что

30