
Кулик Введение в теорию квантовых вычислений Книга 2 2008
.pdf
получим, что амплитуда bω |
состояния |
|
ω |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
||||||||||||
bω =2< a >−aω = |
2 |
|
− |
2 |
+ |
1 |
= |
|
1 |
|
− |
4 |
> |
1 |
|
||||
|
1 |
|
|
|
|
|
|
3 |
|
|
|
(3.32) |
|||||||
|
|
N |
|
|
N |
||||||||||||||
|
N |
|
N |
|
|
|
|
N |
|
|
N |
|
|
||||||
возрастает по сравнению с начальным значением 1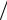 N , если, конечно, N > 2 .
N , если, конечно, N > 2 .
Таким образом, применение оператора G к начальному состоянию (3.21) «поворачивает» вектор этого состояния в направлении к
искомому состоянию ω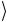 . Уже из результата (3.32) первой итера-
. Уже из результата (3.32) первой итера-
ции Гровера можно понять, что амплитуда состояния ω возрастает пропорционально числу итераций. Поэтому после числа шагов порядка N состояние ω
возрастает пропорционально числу итераций. Поэтому после числа шагов порядка N состояние ω будет входить с коэффициентом,
будет входить с коэффициентом,
близким к единице, а амплитуды остальных состояний будут стремиться к нулю. После этого надо только измерить состояние регистра и получить двоичную запись числа ω . На этом процедура квантового поиска заканчивается.
Приведенные здесь качественные рассуждения по поводу возрастания амплитуды вероятности искомого состояния ω и оцен-
и оцен-
ка числа шагов как N показывают, что алгоритм квантового поиска в неупорядоченной базе данных дает полиномиальное ускорение по сравнению с классическим вычислением.
Алгоритм Гровера допускает точное описание для произвольного числа итераций, к которому мы сейчас перейдем.
Многократная итерационная процедура
Рассмотрим процедуру многократного применения оператора Гровера G =U sU ω . В начальном состоянии Ψ0 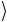 (3.21) все коэф-
(3.21) все коэф-
фициенты одинаковые. Каждое последующее состояние Ψk +1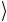
231

получается из предыдущего Ψk  под действием оператора G :
под действием оператора G :
|
|
|
|
|
|
|
Ψk +1 = G |
|
Ψk |
, |
k = 0,1,2,… |
|
|
(3.33) |
|||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Напомним результат первой итерации |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
∑ |
|
|
|
1 |
|
|
|
|||
|
Ψ1 = G |
Ψ0 =U sU ω |
Ψ0 |
=U s |
|
|
x − |
|
|
ω |
= |
||||||||||||
|
|
|
|
||||||||||||||||||||
= ∑bx |
|
x +bω |
|
ω , |
|
|
|
N x≠ω |
|
|
|
N |
|
|
(3.34) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
x≠ω |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
где, согласно (3.24) – (3.32), |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
b |
= 2 < a > − |
|
, |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
x≠ω |
|
|
|
|
|
|
|
|
N |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
b = 2 < a > + |
|
1 |
|
, |
|
|
|
|
(3.35) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
ω |
|
|
|
|
|
|
|
N |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
< a |
>= |
1 |
|
|
− |
2 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
. |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
N |
|
N |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Отметим, что все коэффициенты bx≠ω одинаковые, т.е. не зависят
от x. Это свойство будет иметь место и при всех последующих итерациях, т.е. на каждом шаге будет своя, но одинаковая для всех x ≠ ω амплитуда состояний. Кроме того, все амплитуды являются действительными, так как рассматриваемые унитарные преобразования описываются действительными матрицами и начальные значения амплитуд тоже действительные. Для k-ой итерации обозначим одинаковые действительные амплитуды всех состояний с
x ≠ ω как αk , а действительную амплитуду состояния с x =ω как
βk , т.е.
Ψk = αk ∑ |
|
x +βk |
|
ω . |
(3.36) |
|
|
x≠ω
232

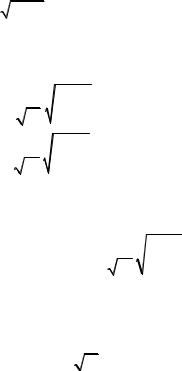
ные коэффициенты αk и βk для любого k подчиняются условию
(N −1)αk2 +βk2 =1. |
(3.41) |
Сделаем подстановку
αk = |
1 |
cosθk , βk = sin θk |
(3.42) |
|
N −1 |
||||
|
|
|
и выразим рекуррентные соотношения (3.39) через углы θk и θk +1 :
|
|
|
2 |
|
2 |
|
|
|
|
1 |
|
sin θk ≡ cos(θk + 2θ), |
||
cosθk +1 |
= 1 |
− |
|
cosθk − |
|
|
1 |
− |
|
|
|
|||
|
N |
|
N |
|||||||||||
|
|
|
N |
|
|
|
|
(3.43) |
||||||
|
|
|
2 |
|
2 |
|
|
|
|
1 |
|
|||
|
|
|
|
|
|
|
cosθk ≡ sin (θk + 2θ), |
|||||||
sin θk +1 |
= 1 |
− |
|
sin θk + |
|
|
|
1 |
− |
|
|
|
||
|
|
N |
N |
|||||||||||
|
|
|
N |
|
|
|
|
|||||||
где
cos 2θ =1− |
2 |
, |
sin 2θ = |
2 |
1− |
1 |
, |
(3.44) |
|
N |
N |
N |
|||||||
|
|
|
|
|
|
т.е.
sin θ = |
1 |
. |
(3.45) |
|
|||
|
N |
|
|
Из соотношений (3.43) следует, что углы θk образуют арифметическую прогрессию
θk +1 = θk + 2θ. |
(3.46) |
234

При k = 0 имеем α0 = β0 = |
|
|
1 |
(3.40). Тогда из (3.42) получаем |
|
|
|
N |
|||
|
|
|
|
|
|
cosθ0 |
= |
N −1α0 = |
1−1 N, |
||
sin θ0 |
= |
β0 |
=1 N . |
(3.47) |
|
|
|||||
Из сопоставления с (3.45) видим, что |
|
||||
|
|
|
|
θ = θ0 . |
(3.48) |
Следовательно, решение рекуррентных соотношений для величин θk имеет вид:
θk = (2k +1)θ, k = 0,1,2,… |
(3.49) |
Поэтому амплитуды
|
k |
|
1 |
( |
) |
|
k |
( |
) |
|
α |
|
= |
N −1 |
cos |
2k +1 θ , |
β |
|
= sin |
2k +1 θ |
(3.50) |
|
|
|
|
|
|
|
|
|
|
описываются тригонометрическими функциями, аргумент которых линейно растет с увеличением числа итераций. Наличие фактора
1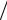 N −1 в коэффициенте αk связано с тем, что N −1 состояний x ≠ ω
N −1 в коэффициенте αk связано с тем, что N −1 состояний x ≠ ω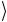 имеют одинаковую амплитуду. При большой базе данных
имеют одинаковую амплитуду. При большой базе данных
N начальный угол θ0 ≈ θ ≈1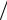 N маленький, и все амплитуды малы. Амплитуда βk искомого состояния ω
N маленький, и все амплитуды малы. Амплитуда βk искомого состояния ω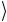 возрастает с каждой итерацией и достигает максимального значения βk =1 при условии (2k +1)θ = π
возрастает с каждой итерацией и достигает максимального значения βk =1 при условии (2k +1)θ = π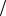 2 , т.е. на «шаге» с номером
2 , т.е. на «шаге» с номером
k = |
π |
θ− |
1 |
, |
(3.51) |
|
4 |
|
2 |
|
|
235 |
|
|
|
|
|

где sin θ = |
1 |
. |
|
||
|
N |
|
Наибольший интерес, конечно, представляет случай большой базы данных, когда N 1. При этом число шагов, необходимое для достижения максимальной, т.е. близкой к единице, амплитуды искомого состояния, определяется выражением
k = |
π |
N − |
1 |
|
N . |
(3.52) |
|
4 |
|
2 |
|
|
|
Таким образом, если повторить итерации ближайшее к величине (3.52) целое число раз, а потом измерить получившееся состояние, то можно с высокой и не зависящей от N вероятностью найти со-
стояние ω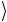 .
.
Принципиальный результат состоит в том, что квантовый поиск требует числа шагов, которое пропорционально квадратному корню из размера базы.
Поскольку в процессе вычислений все амплитуды остаются действительными, всю процедуру квантового поиска можно непосредственно проиллюстрировать с помощью последовательности картинок, изображенных на рис. 3.3.
Они показывают поиск «квантовой иголки в квантовом стоге сена» из шести элементов. Изображены результаты преобразования
амплитуд шести состояний x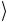 .
.
Первый оператор U ω каждой итерации Гровера меняет знак амплитуды искомого состояния ω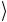 , в данном случае – четвертого
, в данном случае – четвертого
слева. Второй оператор U s осуществляет инверсию амплитуд относительно среднего значения. Здесь N = 6 , поэтому из формулы (3.51) следует, что k 1, 4 . На рисунке отчетливо видно значи-
тельное возрастание амплитуды искомого состояния уже после двух итераций, т.е. после двукратного применения оператора Гровера.
236
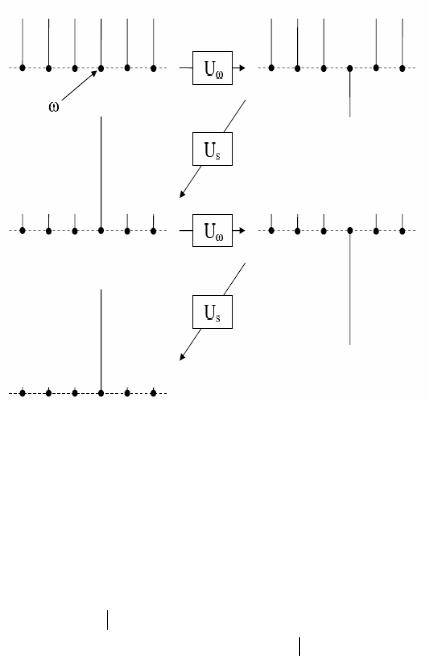
Рис. 3.3
Квантовая схема алгоритма Гровера
Сконструируем квантовую схему, реализующую алгоритм квантового поиска Гровера. Для этого рассмотрим достаточно простой, но, тем не менее, вполне содержательный случай, когда база данных содержит четыре числа 0, 1, 2 и 3, которые в двоичном коде имеют вид x = 00, 01, 10 и 11. Этим числам отвечают четыре базо-
вых состояния x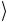 двухкубитового регистра. К этому регистру добавляется еще один вспомогательный кубит y
двухкубитового регистра. К этому регистру добавляется еще один вспомогательный кубит y .
.
237
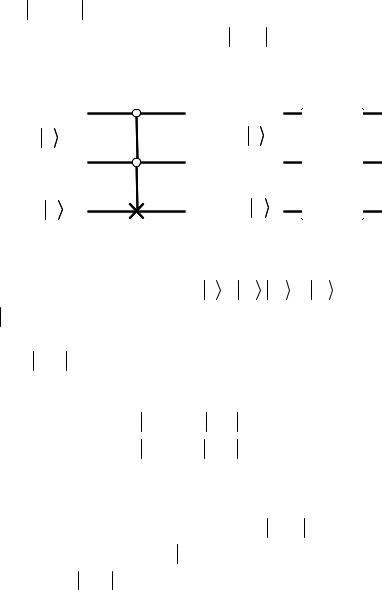
Прежде всего, построим квантовую схему, описывающую действие оператора U fω квантового «оракула» (3.14), т.е.
U fω x
 y
y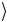 = x
= x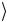
 y f (x)
y f (x)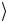 .
.
Если искомое число ω = 0 , т.е. ω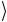 = 00
= 00 , то квантовая схема «оракула» имеет вид модифицированного элемента Тоффоли:
, то квантовая схема «оракула» имеет вид модифицированного элемента Тоффоли:
|
|
|
|
|
x |
|
x |
|
|
|
|
ˆ |
||
|
|
≡ |
|
|
|
|
|
U fω |
|
y |
|
y |
|
|
|
Рис. 3.4 |
|
|
|
Действительно, если x ≠ 0 , т.е. |
x = 01 , 10 |
и 11 , то состояние |
||
y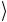 вспомогательного кубита не меняется. Если x = 0, т.е. совпадает с искомым числом, то состояние двухкубитового регистра есть x
вспомогательного кубита не меняется. Если x = 0, т.е. совпадает с искомым числом, то состояние двухкубитового регистра есть x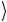 = 00
= 00 , и состояние вспомогательного регистра проходит через операцию NOT:
, и состояние вспомогательного регистра проходит через операцию NOT:
y = 0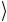 → 1
→ 1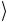 ≡ 0 1
≡ 0 1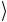 , y =1
, y =1 → 0
→ 0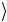 ≡ 1 1
≡ 1 1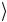 .
.
Квантовые схемы «оракулов» для других значений искомого числа ω строятся аналогичным образом и показаны на рис. 3.5.
Схема (а) отвечает случаю ω =1, т.е. ω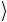 = 01
= 01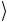 . Управляемый
. Управляемый
(вспомогательный) кубит y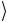 проходит через операцию NOT,
проходит через операцию NOT,
только если x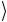 = 01
= 01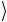 .
.
238

Рис. 3.5 |
|
|
|
|
|
|
|
|
|
|
||
Схемы (б) и (в) отвечают, соответственно, значениям |
ω = 2 и |
|||||||||||
ω = 3, т.е. базисным состояниям регистра данных |
|
10 |
и |
|
11 . В |
|||||||
|
|
|||||||||||
дальнейшем каждая из этих схем изображается |
|
в виде |
|
блока |
||||||||
(«черного ящика»), как показано справа на рис. 3.4 и рис. 3.5. |
||||||||||||
На вход «оракула» подается состояние |
|
Ψ0 |
1 |
|
( |
|
0 − |
|
1 ), ко- |
|||
|
|
|
|
|||||||||
|
2 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
торое описывается выражениями (3.21), (3.15) и приготавливается с помощью однокубитовых операций, показанных на рис. 3.6.
0 |
H |
|
|
|
1 |
|
|
|
|
|
|
Ψ0 |
= |
( 00 |
+ 01 + 10 |
+ 11 ) |
|
|
|
|
2 |
|||||
0 |
H |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
0 |
|
H |
1 |
( 0 |
− 1 ) |
|
|
|
|
2 |
|
|
|||||
|
|
|
|
|
|
|
||
Рис. 3.6
Теперь отдельно обсудим квантовую схему, реализующую оператор U s (3.23) инверсии относительно среднего. В общем случае n-кубитового регистра данных состояние s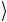 (3.21) получается из
(3.21) получается из
вектора 00…0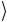 применением оператора H n (см. формулу
применением оператора H n (см. формулу
239
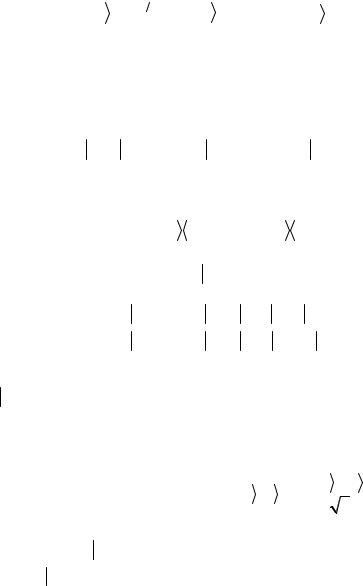
(3.143)), т.е.
|
2n −1 |
|
|
|
||
|
s = 2−n 2 ∑ |
|
x = H n |
|
00…0 . |
|
|
|
|
||||
|
x=0 |
|
|
|
|
|
Подставляя это соотношение в |
(3.23) и учитывая, что |
|||||
H + = H = H −1 , получаем следующее |
выражение для оператора |
|||||
U s :
U s = 2 s
 s −1 = H n (2 00…0
s −1 = H n (2 00…0
 00…0 −1)H n . (3.53)
00…0 −1)H n . (3.53)
Стоящий в круглых скобках оператор
2 |
|
00 0 00 0 |
|
−1 ≡ 2 |
|
0 0 |
|
−1 |
(3.54) |
|
|
|
|
действует на базисные векторы x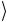 следующим образом:
следующим образом:
x = 0 → 2 0
→ 2 0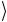
 0 0
0 0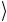 − 0
− 0 = 0
= 0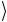 , x ≠ 0
, x ≠ 0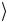 → 2 0
→ 2 0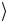
 0 x
0 x − x
− x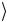 = − x
= − x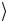 ,
,
т.е. он меняет на противоположную фазу всех состояний, кроме 0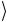 . Другими словами, это оператор условного фазового сдвига. Наглядная интерпретация результата (3.53) достаточно проста. Как
. Другими словами, это оператор условного фазового сдвига. Наглядная интерпретация результата (3.53) достаточно проста. Как
мы знаем, оператор U s осуществляет отражение относительно среднего. Операторы Адамара одинаковым образом поворачивают
|
|
|
|
|
0 ± |
|
1 |
||
|
|
|
|
|
|||||
базисные векторы каждого кубита { |
0 , |
|
1 }→ |
|
|
|
|
|
. После |
|
|
|
|
||||||
|
|
2 |
|
||||||
|
|
|
|
|
|
||||
|
|
||||||||
такого поворота в гильбертовом пространстве операция инверсии относительно s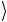 становится преобразованием инверсии относи-
становится преобразованием инверсии относи-
тельно 0 .
.
240

 является нормированным, поэтому действитель-
является нормированным, поэтому действитель-