
Кулик Введение в теорию квантовых вычислений Книга 2 2008
.pdf
2.6. Мультикубитовые гейты
Детальное обсуждение двухкубитовых преобразований, проведенное в предыдущем разделе, содержит все необходимое для понимания того, как сделать заключительный шаг и перейти к общему случаю унитарных преобразований в пространстве состояний произвольного n-кубитового регистра. Эти вопросы составляют содержание данного раздела.
Сначала для наглядности рассматриваются некоторые конкретные трехкубитовые и более сложные гейты. Они представляют в том числе и самостоятельный интерес, поскольку используются как готовые блоки в архитектуре сложных квантовых схем. Демонстрируется также, каким образом эти гейты можно представить с помощью простейших логических элементов, рассмотренных ранее. Затем формулируется окончательное утверждение об универсальном наборе квантовых гейтов.
Трехкубитовые условные операции
Результаты предыдущего раздела показали, насколько полезной оказывается операция Controlled U (обозначим ее, для краткости, с помощью аббревиатуры CU) для конструирования произвольных двухкубитовых преобразований. Обобщением этой условной операции на случай трехкубитовых систем является гейт Controlled
Controlled U ( C2U ), показанный на рис. 2.20.
a

 a
a
b
 b
b
c
 U
U 
 c′
c′
Рис. 2.20
191
Теперь есть два управляющих кубита, которым отвечают две верхние линии с темными кружками, и один управляемый кубит, представленный нижней линией с изображением однокубитовой уни-
тарной операции ˆ
U .
Гейт C2U действует таким образом, что управляемый кубит

 подвергается унитарному преобразованию ˆ в том и только c U
подвергается унитарному преобразованию ˆ в том и только c U
том случае, когда оба управляющих кубита находятся в базисном состоянии 1 , т.е. a
, т.е. a = 1
= 1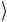 и b
и b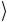 = 1
= 1 . Если хотя бы один из
. Если хотя бы один из
управляющих кубитов находится в состоянии 0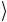 , то управляемый
, то управляемый
кубит остается в исходном состоянии. Как обычно, состояния управляющих кубитов во всех случаях остаются неизменными. Из
восьми ( 23 = 8 ) базисных векторов трехкубитовой системы операция C2U перемешивает только два, 110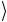 и 111
и 111 . Остальные базисные кэт-векторы не меняются. Мы не будем выписывать в
. Остальные базисные кэт-векторы не меняются. Мы не будем выписывать в
явном виде довольно громоздкую 8×8 матрицу гейта C2U , а просто дадим ее словесное описание. В этой матрице в правом нижнем
ˆ |
u w |
. Что касается ос- |
|
углу стоит унитарная подматрица U = |
|
||
|
v |
z |
|
тальных элементов, то диагональные равны единице, а недиагональные – нулю.
Покажем, что трехкубитовая условная операция C2U может быть выражена через несколько двухкубитовых условных гейтов.
Для этого представим ˆ в виде
U
ˆ ˆ 2 |
(2.225) |
U =V |
квадрата некоторого унитарного оператора ˆ . Последний, тем
V
самым, равен квадратному корню из ˆ и может быть найден в
U
общем виде. Действительно, воспользуемся формулой (2.67), кото-
рая выражает произвольный унитарный оператор ˆ через матрицу
U
192
|
|
ˆ |
|
|
|
|
|
|
|
|
|
|
|
|
|
конечных вращений R(Φ, n) , т.е. |
|
|
|
|
|
|
|
|
|||||||
|
ˆ |
|
iα ˆ |
|
|
|
|
|
iα i |
Φ |
|
|
|
|
|
|
= e |
(Φ, n) = e |
2 nσ |
. |
|
|
|||||||||
|
U |
R |
|
e |
|
|
|
|
|||||||
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
α |
Φ |
|
|
α |
|
|
|
|
|
|
ˆ |
ˆ |
1 2 |
= e |
i |
|
e |
i 4 nσ |
= e |
i 2 |
ˆ |
Φ |
|
|
||
2 |
(2.226) |
||||||||||||||
V |
= (U ) |
|
|
|
|
R |
|
, n . |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
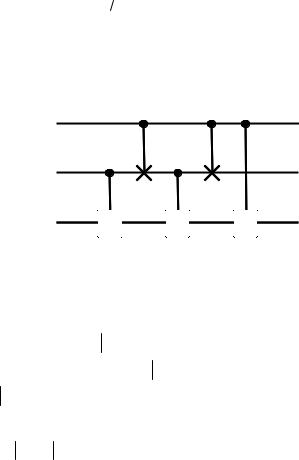
С помощью двухкубитовых условных операций CNOT, CV и CV + квантовая схема гейта C2U может быть представлена в виде
V |
V + |
V |
Рис. 2.21
Проверим, что это схема действительно описывает операцию C2U и эквивалентна той, что изображена на рис. 2.20. Пусть состояние
на входе имеет вид 1
 1
1
 c
c , т.е. оба управляющих кубита нахо-
, т.е. оба управляющих кубита нахо-
дятся в базисном состоянии 1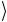 , а состояние управляемого кубита есть c
, а состояние управляемого кубита есть c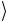 . Сначала CV переводит управляемый кубит в состояние
. Сначала CV переводит управляемый кубит в состояние
ˆ 
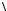 . Последующая операция CNOT меняет состояние второго
. Последующая операция CNOT меняет состояние второго
V c
кубита 1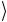 → 0
→ 0 , и он не воздействует на управляемый кубит, т.е.
, и он не воздействует на управляемый кубит, т.е.
операции ˆ + нет. Следующий гейт CNOT возвращает второй ку-
V
193
бит в исходное состояние 1 , а CV переводит управляемый кубит
, а CV переводит управляемый кубит
|
ˆ |
|
c в |
ˆ |
2 |
|
|
c |
|
|
ˆ |
|
|
|
c . Таким образом, |
цепочка пре- |
|||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
из состояния V |
|
V |
|
|
|
|
=U |
|
|
|
|||||||||||||||||||||||||||
образований |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
11 |
|
c → |
|
|
|
|
|
ˆ |
|
c )→ |
|
|
|
ˆ |
|
c |
)→ |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
11 (V |
|
10 (V |
|
|
|
|
|
|
(2.227) |
||||||||||||||||||||||||||
|
|
|
→ |
|
11 |
( |
ˆ |
|
|
c |
) |
→ |
|
|
11 |
( |
ˆ 2 |
|
c |
) |
= |
|
11 |
( |
ˆ |
|
c |
) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
V |
|
|
|
|
V |
|
|
|
|
U |
|
|
|
||||||||||||||||||||
дает результат действия операции C2U . Проведем еще одну контрольную проверку, например, для начального состояния 10
 c
c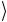 .
.
Поскольку второй кубит в состоянии 
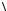 , то первый оператор ˆ
, то первый оператор ˆ
0 V
на управляемый кубит не действует. Гейт CNOT меняет состояние второго кубита 0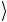 → 1
→ 1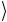 , и на управляемый кубит действует опе-
, и на управляемый кубит действует опе-
ˆ + |
, т.е. |
|
ˆ + |
|
c . Еще один гейт CNOT возвращает |
|
|
||||
ратор V |
|
c →V |
|
второй кубит в исходное состояние 0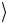 , а операция CV подвергает
, а операция CV подвергает
состояние |
управляемого |
|
кубита |
|
|
|
|
|
ˆ |
||||||||||||||||||||
|
|
преобразованию V , т.е. |
|||||||||||||||||||||||||||
ˆ + |
|
c |
|
ˆ ˆ + |
|
c = |
|
c . Поэтому данная цепочка преобразований |
|||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||
V |
|
→VV |
|
|
|
||||||||||||||||||||||||
|
|
|
|
10 |
|
c → |
|
11 |
|
c → |
|
ˆ + |
|
|
c )→ |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
11 (V |
|
|
|
|
|
(2.228) |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
( |
ˆ + |
|
) |
|
|
|
|
( |
ˆ ˆ + |
) |
|
|
|||||
|
|
|
|
|
|
|
|
|
→ |
10 |
c |
|
→ |
10 |
|
c = |
10 |
c |
|
||||||||||
|
|
|
|
|
|
|
|
|
V |
|
|
VV |
|
||||||||||||||||
не меняет состояние системы, как и должно быть согласно операции C2U в том случае, когда один из управляющих кубитов сначала был в состоянии 0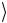 . Аналогичным образом проверяются и
. Аналогичным образом проверяются и
все остальные варианты начального состояния системы.
Как было показано в предыдущем разделе, все двухкубитовые операции могут быть представлены с помощью однокубитовых преобразований и фундаментального гейта CNOT. С учетом квантовой схемы, представленной на рис. 2.21, данное утверждение справедливо и для трехкубитового гейта Controlled Controlled U.
194

Гейт Тоффоли
Рассмотрим специальный случай преобразования C2U , когда
ˆ |
является однокубитовым гейтом NOT. Преобразование |
U =σ1 |
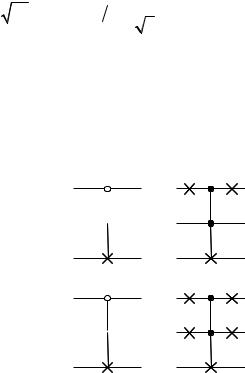
Controlled Controlled NOT ( C2 NOT ) называется Тоффоли-гейтом
и изображается схемой, представленной на рис. 2.22.
a
 a
a
b
 b
b
c
 c′
c′ = c (a b)
= c (a b)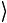
Рис. 2.22
Эта операция действует таким образом, что управляемый кубит c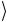 испытывает операцию NOT только в том случае, когда оба управляющих кубита a
испытывает операцию NOT только в том случае, когда оба управляющих кубита a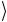 и b
и b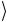 находятся в состоянии 1
находятся в состоянии 1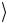 . В остальных
. В остальных
случаях состояние c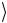 не меняется.
не меняется.
С точки зрения квантовых вычислений, гейт Тоффоли осуществляет с битами a, b и c операцию
c (a b), |
(2.229) |
результат которой записан в выходном состоянии управляемого регистра c′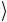 = c (a b)
= c (a b)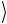 . Символ , как уже говорилось, озна-
. Символ , как уже говорилось, озна-
чает сложение по модулю 2. Это классический логический элемент (см. книгу 1) XOR (исключающее ИЛИ). Символ a b обозначает произведение битов a и b и соответствует классическому логическому элементу AND (И). Из (2.229) видно, что если либо a, либо b,
195
либо оба бита равны нулю, то c (a b)= c . Если же a = b =1, то c (a b) = c 1 = c , где c есть НЕ с, т.е. c =1 для c = 0 и
c = 0 для c =1.
Заметим, что в классических вычислениях элемент Тоффоли является универсальным обратимым гейтом, с помощью которого можно моделировать все необходимые логические элементы. Что же касается квантового гейта Тоффоли, то в соответствии с общей схемой, представленной на рис. 2.21, он сводится к некоторому
|
|
|
|
ˆ |
=σ1 , |
то в эту схему |
||||
набору двухкубитовых операций. Так как U |
||||||||||
входит оператор |
|
|
|
|
|
|
|
|
||
ˆ |
|
|
1+iσ1 |
|
π |
|
|
|
|
|
V = |
σ1 = exp(−iπ 4) |
2 |
= exp i |
4 |
(σ1 |
−1) . |
(2.230) |
|||
|
|
|
|
|
|
ˆ 2 |
|
|||
Непосредственным |
умножением можно убедиться, что |
=σ1 |
||||||||
V |
||||||||||
(см. также задачу 13 в конце раздела 2.2).
Трехкубитовый гейт Тоффоли оказывается очень полезным и удобным элементом при конструировании квантовых схем. При этом используются и модифицированные формы гейта Тоффоли, например такие, которые показаны на рис. 2.23 вместе с эквивалентными схемами.
(a)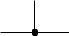 =
=
(б) 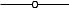 =
=
Рис. 2.23
196
Для схемы (а) управляемый кубит проходит через операцию NOT, когда управляющие кубиты находятся в состоянии 10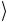 , а в случае
, а в случае
(б) это происходит для управляющих кубитов в состоянии 00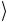 .
.
Приведем два примера использования гейта Тоффоли как элемента квантовых схем.
Рассмотрим трехкубитовое унитарное преобразование, которое перемешивает с помощью подматрицы σ1 только два базисных
состояния системы, 101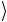 и 110
и 110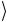 , а остальные базисные векторы
, а остальные базисные векторы
не меняются. Эта операция называется управляемым обменом, или элементом Фредкина. Квантовую схему такого преобразования будем изображать в виде
Соединенными между собой знаками на линиях второго и третьего кубитов обозначена операция обмена значениями битов, которая происходит, если первый (управляющий) кубит находится
в состоянии 1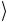 . Поскольку элемент Фредкина перемешивает толь-
. Поскольку элемент Фредкина перемешивает толь-
ко два базисных состояния, он представляет собой двухуровневое преобразование, о которых мы говорили в предыдущем разделе, и описывается двухуровневой матрицей. В данном случае эта 8×8 матрица имеет вид
|
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
|
||||||||
|
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
|
|
|
||||||||
|
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
, |
|
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
|
|
|
||||||||
|
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
|
|
|
||||||||
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
|
|
|
||||||||
|
|
|
|
197 |
|
|
|
|
|
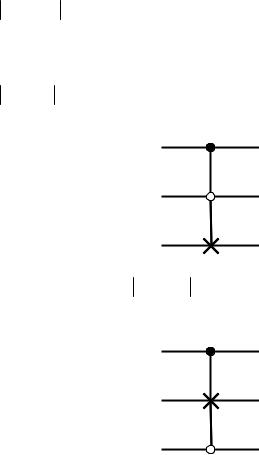
а пунктиром выделена подматрица σ1 . Явный вид столь громозд-
кой матрицы нам не нужен, а приведен он здесь только для полноты картины.
Идея конструктивного построения квантовой схемы уже была изложена в предыдущем разделе. Перемешиваемые состояния
101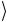 и 110
и 110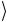 отличаются значениями двух битов – второго и третьего. Чтобы эффективно использовать подматрицу σ1 как од-
отличаются значениями двух битов – второго и третьего. Чтобы эффективно использовать подматрицу σ1 как од-
нокубитовый гейт, надо выровнять значения одного из этих битов, например третьего. С этой целью поменяем местами состояние
101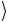 и 100
и 100 , что делается с помощью модифицированного Тоф- фоли-гейта
, что делается с помощью модифицированного Тоф- фоли-гейта
Далее в состояниях 100 и 110
и 110 применяем операцию NOT ко
применяем операцию NOT ко
второму кубиту при фиксированных состояниях первого и третьего кубитов. Это делается опять с помощью Тоффоли-гейта вида
Возвращение на место переставленных состояний осуществляется тем же Тоффоли-гейтом, который применялся на первом шаге, так как Тоффоли-гейт совпадает со своим обратным. Таким образом, вся схема элемента Фредкина можетбытьпредставленаспомощью
198
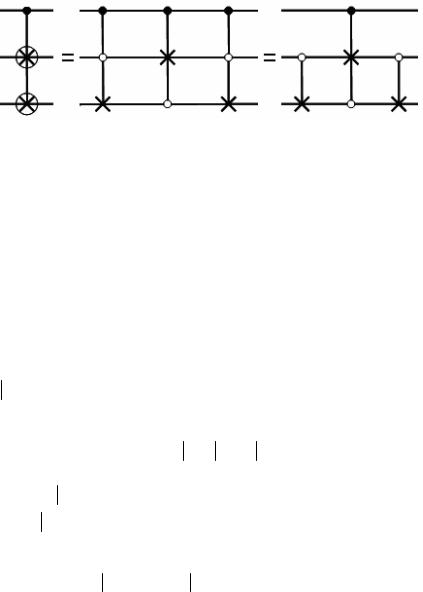
трех гейтов Тоффоли, как это было описано выше и показано в середине рис. 2.24.
Рис. 2.24
Справа на рис. 2.24 показана эквивалентная схема, в которой первый и третий Тоффоли-гейты заменены двухкубитовыми опера-
циями CNOT . Проверка правильности действия этих схем предоставляется читателю.
Второй пример демонстрирует применение Тоффоли-гейта для построения квантовой схемы условной операции U с произволь-
ным числом управляющих кубитов, т.е. гейта CnU .
Пусть, для простоты рассуждений, число управляющих кубитов n=3. Нас интересует условная операция такая, что управляемый кубит подвергается воздействию унитарного однокубитового опе-
ратора ˆ , когда все управляющие кубиты находятся в состоянии
U
1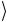 . В других случаях состояние управляемого кубита не меняется.
. В других случаях состояние управляемого кубита не меняется.
В квантовой схеме, показанной на рис. 2.25, три верхние линии отвечают управляющим кубитам, которые находятся в начальных
состояниях, соответственно a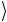 , b
, b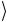 и c
и c . Далее нарисованы линии двух вспомогательных кубитов, находящихся сначала в состоянии 0
. Далее нарисованы линии двух вспомогательных кубитов, находящихся сначала в состоянии 0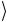 . Наконец, последняя линия изображает управляемый
. Наконец, последняя линия изображает управляемый
кубит d .
.
После первого гейта Тоффоли, согласно (2.229), состояние первого вспомогательного кубита, который является управляемым,
принимает вид 0 (a b) = a b
= a b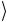 .
.
199
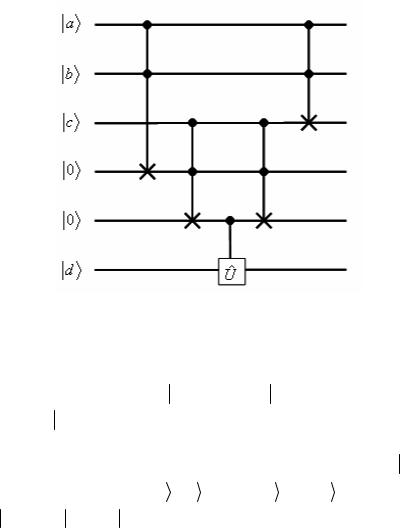
Рис. 2.25
Следующий Тоффоли гейт сделает состояние второго вспомогательного кубита равным 0 (a b c) = a b c
= a b c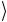 . Это будет со-
. Это будет со-
стояние 1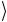 тогда и только тогда, когда a = b = c =1. Второй вспомогательный кубит является управляющим для двухкубитовой операции CU над интересующим нас управляемым кубитом d
тогда и только тогда, когда a = b = c =1. Второй вспомогательный кубит является управляющим для двухкубитовой операции CU над интересующим нас управляемым кубитом d .
.
Поэтому, если |
|
a b c = |
|
1 |
, то |
|
ˆ |
|
d . Если же |
|
|
|
|
||||||
|
|
|
d →U |
|
a b c = 0
= 0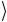 , то d
, то d не изменится. В этом и состоит операция
не изменится. В этом и состоит операция
C3U . Два Тоффоли-гейта в правой части схемы возвращают вспомогательные кубиты в исходное состояние. В принципе, это нужно делать, так как вспомогательные кубиты могут быть использованы для других действий до или после рассмотренной нами операции.
200
