
Кулик Введение в теорию квантовых вычислений Книга 2 2008
.pdf
Условные операции с несколькими управляемыми кубитами описываются схемами вида
≡
Рис. 2.26
Здесь операция CNOT применяется ко второму и третьему кубитам.
Универсальный набор гейтов
Вернемся к общей постановке вопроса об универсальном наборе гейтов, с помощью которых можно описать любую унитарную операцию в пространстве состояний n-кубитового регистра.
Как уже говорилось, любую унитарную матрицу можно представить в виде конечного произведения двухуровневых матриц. Формальное доказательство этого свойства приведено в задаче 4 в конце раздела 2.5. Поэтому достаточно рассмотреть произвольную
унитарную двухуровневую |
2 |
n |
×2 |
n |
|
|
|
|
|
ˆ |
|
||||||
|
|
матрицу M , которая сущест- |
|||||||||||||||
венно перемешивает только два базисных вектора |
|
||||||||||||||||
n-кубитовой |
|
s ≡ |
|
sn−1sn−2 ...s0 |
и |
|
t |
≡ |
|
tn−1tn−2 ...t0 |
(2.231) |
||||||
|
|
|
|
||||||||||||||
системы с |
помощью |
унитарной подматрицы |
|||||||||||||||
ˆ |
u |
w |
и не затрагивает остальную часть базиса. Как обычно, |
||||||||||||||
U = |
|
|
|||||||||||||||
|
v |
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(sn−1sn−2 ...s0 ) |
и (tn−1tn−2 ...t0 ) |
|
есть двоичные записи чисел s и t, |
||||||||||||||
которые нумеруют базисные векторы. Пусть, для определенности, s < t .
201

|
ˆ |
|
|
|
|
|
|
Тогда матрица M имеет вид |
|
|
|
|
|||
|
|
|
s |
|
t |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
0 |
0 |
|
|
|
|
|
|
|
|
||
|
|
1 |
0 |
|
0 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
||
|
s … … 0 u 0 |
0 w 0 |
|
|
|||
|
|
|
0 |
1 |
0 |
|
|
|
|
|
|
. (2.232) |
|||
ˆ |
|
|
|
0 |
|||
|
0 |
|
|
|
|||
M = |
|
0 |
|
|
|
||
|
|
|
|
1 0 |
|
|
|
|
t … … 0 v 0 |
0 z 0 … |
|
||||
|
|
|
|
|
0 1 |
|
|
|
|
0 |
|
0 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
Номера строк и столбцов, на которых располагаются элементы
× матрицы ˆ , отмечены числами ( ) и ( ). В общем случае со- s t
2 2 U
стояния s и t
и t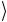 отличаются значениями нескольких битов. Для
отличаются значениями нескольких битов. Для
того чтобы применить оператор ˆ как однокубитовое преобразо-
U
вание, надо чтобы перемешиваемые состояния отличались значением только одного бита. Для этого можно последовательно пере-
ставлять вектор s с другими базисными векторами до тех пор,
с другими базисными векторами до тех пор,
пока все значения его битов, кроме одного, не выровняются с t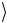 .
.
На каждом шаге последовательности перестановок меняется значение только одного бита. Поэтому такое преобразование реализу-
ется с помощью гейтов условных операций типа Ck NOT . Те кубиты, которые не меняются, являются управляющими. Тот кубит, значение которого надо изменить, является управляемым, и он проходит через операцию NOT. Цепочка преобразований, в ходе которых каждое следующее двоичное число отличается от преды-
202
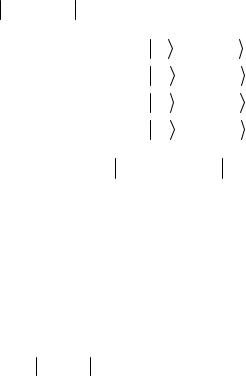
вид 000 → 001
→ 001 → 011
→ 011 и реализуется с помощью двух Тоф-
и реализуется с помощью двух Тоф-
фоли-гейтов. В результате состояния 011 и 111
и 111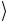 отличаются значением одного бита и могут быть перемешаны с помощью опе-
отличаются значением одного бита и могут быть перемешаны с помощью опе-
рации C2U . При этом второй и третий кубиты являются управляющими, а управляемый первый кубит подвергается однокубито-
ˆ |
u w |
. Квантовая схема |
|
вому унитарному преобразованию U = |
|
||
|
v |
z |
|
изображена на рис. 2.27
U |
Рис. 2.27
Мы видим, таким образом, что матрица ˆ может быть выраже-
M
на с помощью операций Ck NOT и CkU . Сами же эти операции могут быть записаны, как мы знаем из предыдущего раздела, с помощью однокубитовых преобразований и двухкубитового гейта CNOT, которые, тем самым, составляют универсальный набор гейтов (Ди Винченцо, 1995 г.). Тот факт, что нужен только один двухкубитовый гейт и не нужны никакие специальные многокубитовые гейты, очень важен. Формальные математические унитарные преобразования наполняются содержанием по мере их физической реализации на основе того или иного гамильтониана. Если были бы нужны сложные гамильтонианы с произвольными многочастичными взаимодействиями, то о перспективах квантовых вычислений даже с небольшим числом кубитов было бы вообще трудно говорить.
Оценим число универсальных логических гейтов – однокубитовых и CNOT элементов, необходимых для реализации унитарной операции общего вида в пространстве состояний n-кубитового регистра.
204
Напомним, что произвольную унитарную матрицу 2n ×2n мож-
но представить в виде произведения порядка 22n двухуровневых матриц (см. задачу 4 в конце раздела 2.5). Далее, двухуровневое унитарное преобразование осуществляется, как было показано вы-
ше, с помощью многокубитовых условных операций Ck NOT и
CkU . При k n требуется порядка 2n таких операций. Каждую указанную многокубитовую условную операцию можно осуществить с помощью порядка n однокубитовых преобразований и гейтов CNOT. Перемножая все эти числа, получаем окончательную оценку, что требуемое количество универсальных логических гей-
тов составляет величину порядка n2 22n . При больших n это экспоненциально большая величина. В принципе, есть задачи, которые могли бы потребовать столь большого ресурса, если их решать, идя «напролом». Преодоление этих трудностей есть проблема поиска быстрых квантовых алгоритмов.
Классические и квантовые вычисления
Употребляя термин «квантовая информация», мы фактически отождествляем ее с понятием квантового состояния n-кубитового регистра, которое описывается абстрактным кэт-вектором гильбертова пространства. Взаимодействие кубитов с внешними полями, либо между собой, либо с другой физической системой приводит к изменению квантового состояния, в результате чего квантовая информация модифицируется. В условиях унитарной эволюции квантовая информация не теряется. Поскольку в реальных физических системах есть много причин, нарушающих унитарную эволюцию, первостепенное значение имеет разработка методов, минимизирующих такие нарушения, а также способов контролировать и исправлять возникающие ошибки.
Основные логические операции над кубитами могут быть реализованы с помощью тех или иных физических механизмов. В разделе 2.2 мы обсудили этот вопрос применительно к однокубитовым операциям. Реализация гейта CNOT будет рассмотрена в главе 4.
Проанализированные выше примеры квантовых схем показывают, что с их помощью можно, в принципе, контролируемым
205

образом манипулировать квантовой информацией. О таких процессах принято говорить как о квантовых вычислениях, а устройство, их выполняющее, будем называть квантовым вычислителем.
По сравнению с классическими вычислениями процессы манипулирования квантовой информацией содержат в себе принципиально новое качество. Мы уже отмечали выше такие факторы как экспоненциально большую емкость многокубитового квантового регистра, возможность квантового параллельного вычисления, а также, например, несовместимую с классическими представлениями степень корреляции в перепутанных квантовых состояниях. При этом вполне естественным представляется желание, приобретая что-то новое, не потерять то лучшее, что было наработано в прежнем. Другими словами, нас интересует, могут ли квантовые схемы воспроизводить классические логические элементы.
Напомним элементарные логические элементы, которые используются в классических вычислительных схемах(см. книгу 1). Это однобитовый элемент NOT (НЕ), который инвертирует значение бита, a → a (НЕ а). Есть целый ряд нужных двухбитовых элементов, которые переводят два входных бита a и b в один выходной c. Вот некоторые из них. Элемент AND (И) выдает 1 тогда и только тогда, когда оба входных бита равны 1, т.е. a,b → c = a b .
Операция XOR (исключающее ИЛИ) складывает входные биты по модулю 2, что обозначается как a b , т.е. a,b → c = a b . Важ-
ную роль играет операция NAND (сокращении от NOT-AND, НЕ- И), которая сначала выполняет над входными битами преобразова-
ние AND, а потом инвертирует получившийся бит, т.е. a,b → a b . Таблица истинности для этой операции выглядит так
ВХОД |
|
|
|
AND |
ВЫХОД |
||
a |
b |
|
|
a b |
c′ = |
|
|
|
|
a b |
|||||
0 |
0 |
|
|
0 |
1 |
|
|
0 |
1 |
|
|
0 |
1 |
|
|
1 |
0 |
|
|
0 |
1 |
|
|
1 |
1 |
|
|
1 |
0 |
|
|
|
|
Рис. 2.28 |
|
|
|
||
|
|
206 |
|
|
|
||

Если один из входных битов равен 1, то результатом операции является обращение второго бита. Так, если a =1, то c′ = a b = b ,
если же b =1, то c′ = a b = a . В классике, конечно, можно получить копию бита. Операция копирования называется FANOUT.
Имеет место важное утверждение, что с помощью элементов NAND и с учетом возможности копирования можно реализовать любые классические логические элементы, т.е. выполнить вычисления любой функции битов.
Операция NOT является обратимой, так как по результату на выходе однозначно восстанавливается значение входного бита. Что же касается упомянутых выше двухбитовых операций AND, XOR, NAND, то они, очевидно, необратимые, поскольку по значению одного выходного бита нельзя восстановить значения двух входных битов. Какая-то информация оказалась утерянной. В этом смысле формальное свойство необратимости операций эквивалентно потере некоторой информации, которую нельзя восстановить, зная только результат операции. Аналогичная потеря информации происходит, например, если просто стереть значение бита. Такую операцию называют примитивным стиранием (примитивный ERASE-гейт).
Пусть одиночный бит представлен как пара равновероятных классических состояний некоторой частицы. Если информация о значении бита оказывается уничтоженной (стертой), то это означает, что объем фазового пространства состояний частицы уменьшился в 2 раза. С точки зрения термодинамики, уменьшение объема фазового пространства системы приводит к уменьшению ее
статистической энтропии на величину kБ ln 2 , где постоянная Больцмана kБ связана с единицами, в которых измеряется энтро-
пия1. Если в нашей системе, которая находится вместе с окружающей средой при температуре T, происходит адиабатический процесс возвращения объема фазового пространства к исходному значению, то это приведет к выделению в окружающую среду количе-
1В теоретической физике энтропия часто измеряется в единицах энергии,
икоэффициент kБ отсутствует.
207
ства теплоты kБT ln 2 . В более общем случае можно сказать, что при стирании компьютером одного бита информации энтропия окружающей среды возрастает не менее, чем на kБ ln 2 , т.е. в среду диссипирует энергия ≥ kБT ln 2 . Это утверждение называется
принципом Ландауэра и было сформулировано им в 1961 г. Приведенное выше максимально упрощенное рассуждение при-
звано лишь проиллюстрировать истоки связи между диссипацией энергии и информацией. С принципом Ландауэра связано современное понимание этого вопроса, который восходит к идее демона Максвелла, сформулированной в 1871 г.
Столь пространное обращение к вопросу о необратимости классических логических элементов объясняется тем фактом, что квантовые гейты представляют собой унитарные преобразования, которые безусловно обратимы. Поэтому применимость квантовых схем для воспроизведения классических операций требует дальнейшего анализа.
Ключевым моментом является тот факт, что любой классический элемент можно представить с помощью схемы, содержащей только обратимые операции (Тоффоли Т., 1980 г.). Другими словами, принципиально возможно проводить универсальные вычисления без потери информации. Для наших целей наиболее удобным способом построения обратимых операций является классический элемент Тоффоли.
Действие квантового элемента Тоффоли в системе трех кубитов подробно описано в этом разделе ранее. Поэтому сейчас достаточно кратко напомнить это описание, но уже применительно к классическому регистру, содержащему три бита – два управляющих (a и b) и один управляемый (c), который проходит через операцию NOT, если только a = b =1, т.е. a,b,c → a,b,c′ = c (a b) . Из
алгебры операций следует, что двукратное применение элемента Тоффоли возвращает биты в исходное состояние. Действительно, a,b,c → a,b,c (a b) → a,b,c (a b) (a b) = a,b,c . Это до-
казывает обратимость элемента Тоффоли, который совпадает со своим обратным.
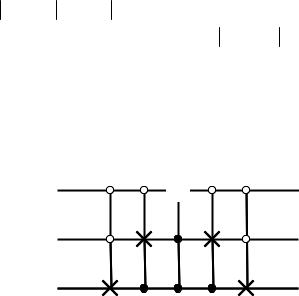
Схема, представленная на рис. 2.29, показывает, что логическая операция NAND реализуется при помощи элемента Тоффоли, если
208

третий бит первоначально установлен в состоянии 1.
a  a
a
b 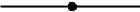 b
b
1 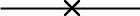
 c′
c′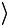 =1 (a b) = a b
=1 (a b) = a b
Рис. 2.29
Два верхних бита являются входными для операции NAND, а третий бит описывает выход. Результат совпадает с описанием действия операции NAND (см. рис. 2.28). Следует подчеркнуть, что сохранение на выходе начальных значений битов a и b обеспечивает, в отличие от стандартного элемента NAND, обратимость. Информация не теряется.
Для универсального набора элементов нужна еще операция FANOUT. На рис. 2.30 показана ее реализация на основе элемента Тоффоли.
Рис. 2.30
Второй бит является входным для операции FANOUT. Выход описывается вторым и третьим битами, которые теперь дают два таких же бита как и входной.
Поскольку квантовый элемент Тоффоли меняет базисные состояния a
 b
b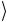
 c
c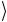 трехкубитового регистра точно таким же обра-
трехкубитового регистра точно таким же обра-
зом, как это делает со значениями битов классический элемент Тоффоли, квантовый вычислитель может выполнить любые вы-
209

числительные операции, возможные на классическом компьютере. Это означает, в том числе, что для квантовых вычислений можно использовать, если нужно, все алгоритмы, разработанные для классических устройств. В этом результате нет ничего неожиданного.
В разделе 2.3, говоря о квантовом параллелизме, мы вынесли за рамки обсуждения вопрос о том, как сконструировать унитарное
преобразование ˆ , осуществляющее вычисление функции ( ),
U f f x
аргумент которой представляет двоичную запись числа x. Теперь можно ответить на этот вопрос следующим образом.
Возьмем такую классическую схему вычисления функции битов f(x), в которой все универсальные логические элементы представлены с помощью классического обратимого элемента Тоффоли. Тогда аналогичная схема с квантовыми элементами Тоффоли будет
осуществлять интересующее нас унитарное преобразование ˆ
U f .
На рис. 2.31 эта операция изображена в виде блока, у которого есть
два входа и два выхода. Операция ˆ действует на квантовом ре-
U f
гистре x
 0
0 , состоящем из двух регистров x
, состоящем из двух регистров x и 0
и 0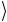 . Первый из
. Первый из
них есть регистр данных, в котором представлены состояния, изображающие числа x. Второй регистр, первоначально находящийся
в состоянии 0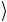 , называется регистром значений, и в него записы-
, называется регистром значений, и в него записы-
ваются числа ( ) в двоичном представлении. Действие ˆ на ба- f x U f
зисные состояния x
 0
0 имеет вид
имеет вид
ˆ |
x 0 = x f (x) . |
(2.234) |
U f |
Если n-кубитовый регистр данных первоначально находится в состоянии (2.143)
Ψ0 = 2− |
n 2n −1 |
|
2 ∑ x , |
(2.235) |
x=0
то состояние системы на выходе описывается кэт-вектором
|
|
|
|
|
|
2n −1 |
||||
ˆ |
|
Ψ0 |
|
0 = 2 |
−n 2 |
∑ |
|
x |
|
f (x) , (2.236) |
|
|
|
|
|||||||
out =U f |
|
|
|
|
|
|||||
x=0
210

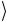 к
к  . Тогда код Грея выглядит так
. Тогда код Грея выглядит так переходит в
переходит в  , и двоичная запись числа
, и двоичная запись числа 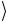 и
и 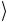 , т.е. имеет вид
, т.е. имеет вид