Кулик Введение в теорию квантовых вычислений Книга 2 2008

ции. Амплитуда a0 содержит сумму различных вкладов. Для постоянной функции f интерференция этих вкладов оказывается конструктивной и дает значение a0 =1. Напротив, для сбалансированной функции f интерференция является деструктивной, и амплитуда a0 обращается в нуль.

В качестве забавной иллюстрации алгоритм Дойча-Джозса можно переложить на язык квантовой игры. Играют Алиса и Боб, как обычно именуют участников коммуникационной сети. Алиса

посылает Бобу какие-то числа x из промежутка от 0 до 2n −1. Боб для каждого числа вычисляет функцию f (x) , которая может при-

нимать только два значения: 0 или 1. Вычисление делается с помощью унитарного преобразования, а вычисляемая функция может быть только либо постоянной, либо сбалансированной. Результаты вычислений Боб посылает Алисе. Спрашивается, сколько ответов нужно Алисе, чтобы выяснить, какую вычислительную манипуляцию – постоянную или сбалансированную – выполняет Боб?

При классических вычислениях в самом неблагоприятном случае Алисе нужно получить количество ответов Боба, равное 2n-1+1. Если использовать алгоритм Дойча-Джозса, то квантовое вычисление нуждается только в одном запросе.

Задачи

1. Вычислить результат действия преобразования Адамара H n на базисные состояния n-кубитового регистра.

Решение

Результат действия преобразования Адамара H на базисные однокубитовые состояния

H 0	=	0 + 1	и H 1 =	0 − 1
		2		2
			221

можно представить в форме единого выражения

H

c =

1

∑ (−1)cc'

c ' ,

c,c ' = 0,1 .

2 c'=0,1

Пусть

x =

xn−1 xn−2 …x0 ≡

xn−1

xn−2

…

x0 есть базисный век-

тор n-кубитового регистра, в котором, как обычно, состоящая из 0 и 1 цепочка (xn−1 …x0 ) является записью числа x. Тогда

H n x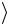 = (H xn−1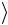)(H xn−2 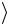)…(H x0 )=

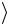= 2−n 2

∑ (−1)xn−1yn−1

yn−1

(−1)xn−2 yn−2

∑

yn−2 …

yn−1 =0,1

yn−2 =0,1

(−1)x0 y0

y0

… ∑

=

y0 =0,1

= 2−n 2

∑ (−1)xn−1 yn−1 +xn−2 yn−2 +…+x0 y0

yn−1

yn−2 …

y0 =

y0 , y1 ,…yn−1

2n

−1

= 2−n 2 ∑(−1)x y

y .

y=0

В этом выражении

y ≡

yn−1 yn−2 …y0 ; состоящая из 0 и 1 цепоч-

ка (yn−1 yn−2 …y0 )

есть двоичная запись числа y; суммирование

ведется по всем значениям y от 0 до 2n −1; символ x y означает

побитовое скалярное произведение xn−1 yn−1 + xn−2 yn−2 +…+ x0 y0 , взятое по модулю 2. Из полученного выражения следует, что матрица оператора H n в n-кубитовом базисе имеет вид

y H n x=2−n2 (−1)x y ,

222

т.е. состоит из чисел ±1, умноженных на общий коэффициент

2−n2 . Поэтому сам оператор H n можно представить в такой форме

H n = 2−n2 ∑(−1)x y yy . x,y

3.2. Алгоритм квантового поиска

Из классической теории информации известно, что для отыскания нужной записи в неупорядоченной базе данных, надо перебрать, в среднем, приблизительно половину элементов базы (см. задачу 1 в конце этого раздела). Так, если в базе данных хранится N записей, то для поиска той, которая нам нужна, потребуется, в среднем, N/2 обращений к функции, определяющей искомый элемент. Это означает, что время поиска пропорционально размеру N этой базы. Типичный пример из жизни, который напрашивается, это телефонная книга, где есть фамилии и номера телефонов. Фамилии расположены в алфавитном порядке, а принадлежащие этим лицам номера телефонов образуют большую неупорядоченную совокупность чисел. Нас интересует фамилия человека, имеющего данный телефонный номер. Это задача поиска некоторого определенного числа среди неупорядоченной совокупности других чисел. Процедура поиска сводится к тому, что надо брать, например, случайно, одно за другим числа x из этой совокупности и сравнивать с тем, которое нам нужно. С математической точки зрения, наличие признака, отличающего нужное число от ненужного, означает, что есть некоторая функция f (x) , которая для интересующего нас

значения x становится равной, например, единице, а для всех других x она отличается от единицы. Это простейший случай, когда задача поиска имеет только одно решение. Для его нахождения классический компьютер должен провести операцию вычисления функции f (x) , в среднем, для половины значений x из области

определения.

В 1996 г. Лов Гровер показал, что если заняться поиском «кван-

223

fω (x) =1.

товой иголки в квантовом стоге сена», воспользовавшись сформулированным им алгоритмом, то время поиска сокращается до ве-

личины, пропорциональной N , т.е. до корневой зависимости от размеров базы. При больших N ускорение процедуры поиска оказывается весьма ощутимым.

Квантовый «оракул»

Сформулируем задачу поиска следующим образом. Пусть имеется некоторая неупорядоченная база данных. Запись каждого элемента этой базы идентифицируется числом x, которое может при-

нимать значения от 0 до N–1, где N = 2n . Задача состоит в том, чтобы найти запись, у которой x равно интересующему нас значению ω . Для простоты полагаем, что в базе данных есть только одна такая запись. Другими словами, надо найти определенное число ω среди некоторой неупорядоченной совокупности чисел x.

С этой целью введем функцию

0,	если x ≠ ω
fω (x) =	если x =ω	,	(3.13)
1,

которая определяет нужную запись, принимая значение 1 только для искомого значения x =ω . Вычислением этой функции занимается «оракул», т.е. тот самый «черный ящик», о котором мы уже говорили в предыдущем разделе. На вход оракула подается значение x, а он выдает результат (3.13). Нас интересует, что нужно сделать, чтобы как можно быстрее получить то значение x, при кото-

ром

При квантовом поиске каждое обращение к «оракулу» может содержать не одно какое-то число x, а суперпозицию состояний, представляющих разные числа. Сам квантовый «оракул» описыва-

ется некоторым унитарным оператором U fω , которой осуществляет обратимое вычисление функции (3.13). По определению, этот оператор действует в пространстве состояний x y системы,

224

состоящей из n +1 кубита. В этой системе к цепочке n log2 N кубитов, представляющей числа x, добавлен еще один вспомогательный кубит y . Действуя на базисное состояние x y , опе-

ратор U fω вычисляет функцию fω (x) , а получившееся значение, 0 или 1, складывает по модулю 2 с y , т.е. осуществляет преобразование:

U fω		x		y =		x		y fω (x) .	(3.14)

Приготовим исходное состояние вспомогательного кубита y в виде

	y =	1	(		0 −		1 ).	(3.15)
		2

Если, как обычно, стартовать с состояния 0 , то кэт-вектор (3.15)

можно получить с помощью двух однокубитовых операций, а именно

0 NOT → 1 H → 12 ( 0− 1).

Рассмотрим теперь действие квантового «оракула» на состояние

x		y =					x (				0 −					1 )					2 :
U fω				x			1		(				0 −					1 )			=	1					x	(		0 fω (x) −		1 fω (x) )=
					2									1							2							(3.16)
= (−1)fω ( x)																	(							1 ).
										x										0 −
														2

Это вычисление аналогично тому, которое мы уже проводили в

225

предыдущем разделе. Действительно, если x ≠ ω , то fω (x) = 0 , и сложение по модулю 2 не меняет состояние второго кубита:

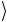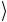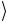0 fω (x)− 1 fω (x) = 0− 1 .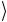

Если же x =ω , то fω (x) =1, так что

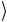0 fω (x)− 1 fω (x) = 1− 0 = −( 0− 1).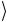

В выражении (3.16) два возможных знака записаны в виде фазового множителя (−1)fω ( x) .

Вектор состояния (3.16) имеет факторизованный вид. Поэтому кэт-вектор второго кубита, который остался в исходном состоянии (3.15), можно в дальнейшем не писать. Тогда действие «оракула»

эквивалентно следующему унитарному преобразованию Uω базисных состояний x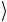 регистра данных:

U ω		x = (−1)fω ( x)		x .	(3.17)

Это преобразование просто меняет на противоположную фазу искомого состояния ω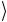 , а фазы остальных базисных векторов оста-

ются неизменными. Поэтому его удобно представить в виде компактного выражения

U ω =1−2		ω ω		,	(3.18)

куда входит только оператор проектирования ωω на состояние

ω . Подействовав этим оператором на произвольное состояние

N −1

Ψ = ∑ax x , (3.19)

x=0

226

получим

N −1

U ω

Ψ = ∑ax (1−2

ω

ω

)

x = ∑ax

x −aω

ω . (3.20)

x=0

x≠ω

Таким образом, оператор Uω ,

изменив знак коэффициента при

состоянии ω и оставив остальные коэффициенты без изменения,

сделал тем самым «метку» на искомом состоянии ω . Поскольку о коэффициентах ax = x Ψ в разложении (3.19) говорят как о про-

екциях вектора Ψ в ортонормированном базисе { x}, то преоб-

разованию (3.20) можно дать наглядную «геометрическую» интерпретацию. Изменение знака проекции на какую-то ось представляет собой отражение в гиперплоскости, ортогональной этой оси (см. задачу 2 в конце этого раздела).

Алгоритм Гровера

Сформулируем теперь идею алгоритма квантового поиска. Мы ищем состояние ω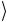 среди всех состояний { x}. Поэтому приго-

товим входной регистр, где записываются числа x, в состоянии

(2.143)

			1	N −1
Ψ0 ≡		s =		∑		x ,	(3.21)
			N x=0

которое, как мы знаем, получается применением преобразования Адамара H n к n-кубитовому состоянию 00…0 . Для этого по-

требуется число операций, которое просто совпадает с числом кубитов n log2 N .

В однородной суперпозиции (3.21) все состояния, изображающие числа x в двоичном коде, представлены с одинаковой вероятностью 1/N. Суть алгоритма Гровера заключается в последователь-

227

ном применении к состоянию регистра, начиная с (3.21), некоторо-

го унитарного оператора G , который модифицирует состояние таким образом, что с каждым шагом амплитуда вероятности со-

стояния ω возрастет. Этот оператор имеет вид

G =U sU ω .

(3.22)

Он включает, помимо уже известного преобразования Uω (3.18), которое выделяет искомое состояние ω , меняя знак соответствующего коэффициента (3.20), еще и оператор

U s = 2		s s		−1,	(3.23)

построенный с помощью внешнего произведения кэт-вектора (3.21). Структура этого оператора похожа на (3.18). В него входит

оператор проектирования на состояние s . Поэтому преобразование (3.23) тоже допускает простую «геометрическую» интерпретацию. Действительно, подействуем оператором U s на произвольное состояние (3.19) и, учитывая определение (3.22) вектора s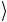 , получим:

N −1

U s

Ψ = (2

s s

−1)∑ax

x =

x=0

N −1

N −1

= 2

s ∑ax s

x −∑ax

x =

x=0

x=0

N −1

2 N −1

= ∑

∑ax' −ax

x .

x=0

N x'=0

228

Здесь на последнем шаге проделаны следующие алгебраические преобразования. В первой сумме использовано значение скалярного произведения

s x = 1N ,

которое следует из разложения (3.21), а потом индекс суммирования обозначен буквой x ' . Для кэт-вектора s использовано раз-

ложение (3.21).

Таким образом, имеем следующее соотношение

		ˆ	N −1		N −1
		U s ∑ax		x = ∑bx		x ,
			x=0		x=0
	в котором новые коэффициенты разложения
			N −1
	bx =	2	∑ ax' −ax ≡ 2 < a > −ax
		N
			x '=0
	содержат не зависящую от x величину
				1	N −1
			< a >=		∑ax .
				N x=0

(3.24)

(3.25)

(3.26)

Ее естественно назвать средним значением амплитуды, с которой x представлено в исходном состоянии Ψ . Если положить, что

ax =< a > +δax ,

(3.27)

т.е. δax имеет смысл отклонения от среднего в исходном состоянии, то коэффициенты после преобразования

bx = a < a > −ax =< a > −δax	(3.28)
229

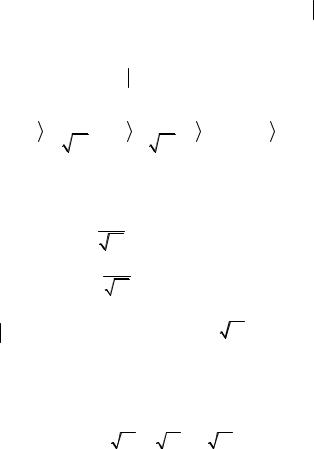
отличаются от исходных значений изменением знака отклонения

от среднего. Поэтому U s называется оператором инверсии относительно среднего.

Покажем, что применение операции Гровера G (3.22) приводит к возрастанию амплитуды вероятности искомого состояния ω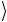 . Поясним это на примере первой итерации, когда происходит однократное воздействие оператора G =U sU ω на начальное однородное суперпозиционное состояние Ψ0 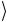. Тогда

U ω

Ψ0 =

1

∑

x −

1

ω ≡ ∑ax

x , (3.29)

N x≠ω

N

x

где

1 , x ≠ ω

a=

x1 . (3.30)

− , x =ωN

Всостоянии Ψ0 средняя амплитуда равна 1 N . После дейст-N

вия оператора Uω средняя амплитуда < a > уменьшилась. Действительно, с учетом (3.30) имеем для N ≥ 2

1

N −1

1 N −1

1

1

2

< a >=

∑ax =

−

=

1

−

. (3.31)

N

N x=0

N

N

N

N

Применяя далее операцию U s , т.е. инвертируя коэффициенты ax (3.30) относительно среднего значения < a > (3.31),

230