Кулик Введение в теорию квантовых вычислений Книга 2 2008
.pdf
в котором, как уже говорилось, представлены значения функции f(x) для всех значений аргумента x. На рис. 2.31 мы показали эту ситуацию, опустив для краткости нормировочный коэффициент
2−n 2 .
2 .
Рис. 2.31
Прежде всего, обратим внимание, что out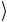 является перепу-
является перепу-
танным состоянием двух регистров. Кроме того, состояние системы на выходе содержит информацию обо всех значениях функции f(x). В такой информации проявляются глобальные свойства функции, например, периодичность и тому подобное. Такие свойства, как мы увидим в следующей главе, играют важную роль в целом ряде квантовых алгоритмов, которые демонстрируют, что с помощью квантовых вычислений можно превзойти возможности классических вычислительных схем.
Список используемой литературы (источники)
1.Ландау Л.Д., Лифшиц Е.М. Квантовая механика. Нерелятивистская теория. — М.: Наука, 2006.
2.Мессиа А. Квантовая механика. Т. 1. — М.: Наука, 1979.
3.Боум А. Квантовая механика. Основы и приложения. — М.: Мир, 1990.
4.Стин Э. Квантовые вычисления. – Ижевск: НИЦ «Регулярная и хаотическая динамика», 2000.
5.Квантовые вычисления: За и против. – Ижевск: Издательский дом «Удмуртский университет», 1999.
6.Квантовый компьютер и квантовые вычисления. – Ижевск: Ижевская республиканская типография, 1999.
7.Нильсен М., Чанг И. Квантовые вычисления и квантовая информация
/Пер. с англ. – М.: Мир, 2006.
211
«Квантовый параллелизм — это фундаментальное свойство многих квантовых алгоритмов.»
М. Нильсен, И. Чанг
Квантовые алгоритмы
Г л а в а 3
КВАНТОВЫЕ АЛГОРИТМЫ
______________________________________________________
Содержание
Задача Дойча. Алгоритм квантового поиска. Квантовый алгоритм Шора. Корреляции ЭПР–Белла в квантовых коммуникационных схемах.
Современный статус теории квантовой информации вообще и квантовых вычислений в частности в значительной степени определяется тем фактом, что известен целый ряд трудных задач, которые можно решить с помощью квантовых методов вычислений гораздо эффективнее, чем это способен сделать любой классический компьютер. В этой главе рассматриваются такие важные квантовые алгоритмы как алгоритм ДойчаДжозса, алгоритм квантового поиска Гровера и алгоритм факторизации Шора, которые особенно ярко демонстрируют разницу между возможностями классических и квантовых вычислений. Открытие этих алгоритмов явилось мощным стимулирующим импульсом к развитию всей области квантовых вычислений. В заключительном разделе данной главы рассматриваются удивительные свойства некоторых квантовых коммуникационных процессов, связанных с передачей квантовой информации. Эти свойства обусловлены несовместимой с классическими представлениями высокой степенью квантовых корреляций между подсистемами в перепутанных квантовых состояниях. Обсуждаются протоколы квантовой плотной кодировки, квантового распределения ключа и процесс квантовой телепортации.
3.1.Задача Дойча
В1985 г. Давид Дойч предложил простой алгоритм, чтобы продемонстрировать потенциальные возможности квантового параллельного вычисления.
Пусть имеется некоторое устройство, на вход которого подается
число x, а оно вычисляет функцию f (x) и выдает ее значение на
выходе. Такое устройство называется «черным ящиком» или «оракулом». Нас интересует, можно ли, приготовив входные данные и узнав результат на выходе, выяснить, что делает «черный ящик»?
213
Задача Дойча, как ее называют, формализует эту проблему следующим образом. Пусть функция f имеет однобитовую область определения, x=0,1, и однобитовую область значений, f(x)=0,1. Другими словами, f (x) отражает один бит в один бит,
{0,1} →{0,1}. Четыре возможные комбинации входных и выход-
ных значений можно разделить на две группы, которые характеризуются разными глобальными свойствами функции f (x) . Для
двух комбинаций f(0)=f(1), и функция f (x) является постоянной. Для двух оставшихся комбинаций f (0) ≠ f (1) , и такую функцию
называют сбалансированной. Спрашивается, сколько раз надо обратиться к «оракулу», чтобы узнать указанное глобальное свойство вычисляемой функции?
Если на входе и выходе имеются классические биты, то ответ очевиден – необходимо обратиться к «оракулу» дважды, получить значения f (0) и f (1) , а затем сравнить их. Для квантового «ора-
кула», который вычисляет функцию f (x) обратимым образом с
помощью некоторого унитарного преобразования U f , действую-
щего на состояния кубитов, ситуация совершенно другая. Как показывает алгоритм Дойча, ответ можно получить, обратившись к «оракулу» только один раз.
Алгоритм Дойча
Поскольку сама функция f (x) может быть, вообще говоря, необратимой, для обеспечения унитарности преобразования надо сохранять входные данные. Поэтому U f действует в пространстве состояний двухкубитовой системы, выполняя преобразование:
x |
|
y →U f |
|
x |
|
y = |
|
x |
|
y f (x) . |
(3.1) |
|
|
|
|
|
Здесь первый кубит описывает входные данные, а второй нужен для записи результата. Вычисления сводятся к нахождению величины f (x) , которая затем складывается по модулю 2 с начальным
значением y второго кубита. Если f (x) = 0 , то второй кубит не
214
меняется. Если же f (x) =1 , то значение второго кубита инвертируется. Заметим, что частный случай соотношения (3.1) для y = 0
совпадает с выражением (2.234), которое уже использовалось ранее.
Если подавать на вход базисные состояния 0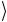 или 1
или 1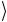 кубита
кубита
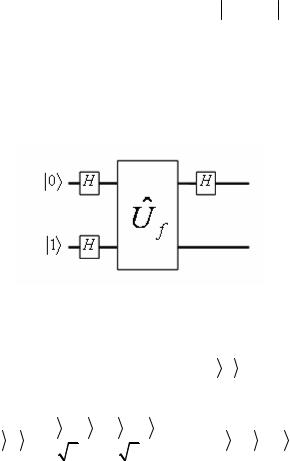
данных, то ситуация не будет отличаться от классической, так как выходное состояние будет содержать информацию о значении функции только для одного x. Идея алгоритма Дойча состоит в том, чтобы состояние на входе было суперпозицией базисных состояний. Схема, реализующая алгоритм Дойча, показана на рис. 3.1.
Рис. 3.1
Первый шаг состоит в том, что стоящие в левой части преобра-
зования Адамара из начального состояния |
0 |
|
1 двухкубитовой |
||||||||||||||||||||||
системы, приготавливают состояние |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
H 2 |
|
0 |
|
1 = |
|
0 + |
|
1 |
|
|
0 − |
|
1 |
= |
1 |
x∑=0,1 |
|
|
x |
( |
|
0 − |
|
1 ). (3.2) |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
2 |
|
|
|
2 |
|
2 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
На это состояние действует «оракул» U f . Возьмем произвольное
слагаемое суммы (3.2) и подействуем оператором U f , используя соотношение (3.1).
215
Тогда
ˆ |
|
x ( |
|
0 − |
|
1 )= |
|
x ( |
|
f (x) − |
|
1 f (x) )= |
||||||
|
|
|
|
|
|
|||||||||||||
U f |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3.3) |
||
|
|
|
|
|
|
= (−1) f ( x) |
|
x ( |
|
0 − |
|
1 ). |
||||||
|
|
|
|
|
|
|
|
|
||||||||||
Вся «изюминка» вычислений заключена в последнем шаге, который показывает, что «оракул» не меняет состояние второго кубита, а зависимость от функции f (x) записывается в виде фазового
множителя (−1)f ( x) . Этот результат легко проверить. Действи-
тельно, |
если f (x) = 0 , |
|
то |
|
x ( |
|
f (x) − |
|
|
1 f (x) |
)= |
|
x ( |
|
0 − |
|
1 ). |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
Если f (x) =1 , имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
x |
( |
|
|
f (x) − |
|
1 f (x) )= |
|
x |
( |
|
|
1 − |
|
|
0 )= − |
|
x |
( |
|
0 − |
|
1 ). |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
Применяя далее операцию U f |
|
к состоянию (3.2), с учетом (3.3) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
получаем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
U f |
1 ∑ |
|
x ( |
|
0 − |
|
1 )= |
1 |
∑(−1)f ( x) |
|
|
|
x ( |
|
0 − |
|
1 )= |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
2 x=0,1 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
(3.4) |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
= |
|
|
|
(−1)f (0) |
|
0 +(−1)f (1) |
|
1 |
( |
|
0 − |
|
1 ). |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
2 |
2 |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
Это состояние имеет факторизованный вид, и второй кубит можно не рассматривать. Поэтому последнее преобразование Адамара просто меняет состояние первого кубита:
H |
|
1 |
(−1)f (0) |
|
0 +(−1)f (1) |
|
|
1 |
|
|
|
= |
|
|
|
|
|||||||||
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
= (−1)f (0) |
|
|
0 + |
|
1 |
+(−1)f (1) |
|
|
0 − |
|
1 |
= |
(3.5) |
|||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
2 |
|
|
|
|
|
2 |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
= |
(−1)f (0) |
+(−1)f (1) |
|
0 + |
(−1)f (0) −(−1)f (1) |
. |
||||||||||||||||||
|
|
||||||||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
216 |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Амплитуда состояния 0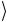 отлична от нуля и равна ±1 тогда и только тогда, когда функция f (x) постоянная, f (0) = f (1) . Если же f (x) — сбалансированная функция, то отлична от нуля и равна
отлична от нуля и равна ±1 тогда и только тогда, когда функция f (x) постоянная, f (0) = f (1) . Если же f (x) — сбалансированная функция, то отлична от нуля и равна
±1 амплитуда состояния 1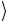 . Вектор состояния (3.5) можно записать в компактном виде как
. Вектор состояния (3.5) можно записать в компактном виде как
± f (0) f (1)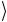 ,
,
поскольку два одинаковых значения складываются в нуль, а два разных — в единицу.
Таким образом, обратившись к «оракулу» один раз и измерив конечное состояние первого кубита, мы с достоверностью определим глобальное свойство функции f (x) .
Физической причиной является принцип суперпозиции и вытекающий из него квантовый параллелизм вычислений, а также интерференция, которая приводит к когерентному суммированию
разных вкладов в амплитуды состояний 0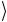 и 1
и 1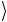 первого кубита.
первого кубита.
Алгоритм Дойча-Джозса
Задача обобщается на случай произвольного n-кубитового регистра данных. Это делается с помощью алгоритма Дойча-Джозса.
«Черный ящик» вычисляет функцию f (x) , область определе-
ния которой есть все числа x от 0 до 2n −1, отвечающие базовым состояниям n-кубитового регистра данных.
Область значений есть один бит, т.е. эта функция осуществляет отображение n битов в один бит, {0,1} n →{0,1}. При этом функция f (x) либо постоянная, т.е. принимает то или иное возможное зна-
чение при всех x, либо сбалансированная, когда она равна нулю точно для половины значений аргумента и, соответственно, равна 1 для остальной половины. Измерив результат на выходе, мы хотим узнать, является ли f постоянной или сбалансированной.
Схема, решающая проблему Дойча-Джозса, показана на рис. 3.2.
217
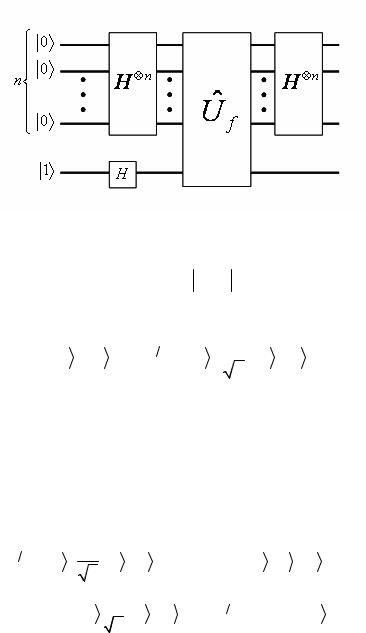
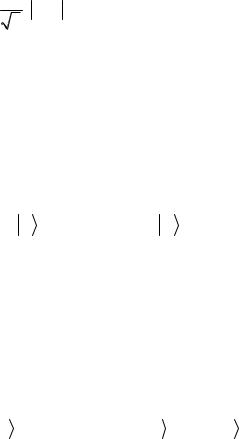

Если f постоянная, т.е. f (x) = c , где c = 0,1, то |
|
a0 = (−1)c = ±1. |
(3.12) |
Поскольку a0 2 =1, то из условия нормировки, которая сохраняется при унитарном преобразовании, следует, что ay≠0 = 0 . Таким образом, если f постоянная, то n-кубитовый регистр с достоверностью будет находиться в состоянии y = 0 ≡ 00…0
≡ 00…0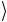 . Если же f — сбалансированная функция, которая для одной половины
. Если же f — сбалансированная функция, которая для одной половины
значений аргумента равна нулю, а для другой – единице, то в сумме (3.11) положительные и отрицательные слагаемые компенсиру-
ют друг друга, и a0 = 0 . Это означает, что будут отличны от нуля, по крайней мере, некоторые коэффициенты ay≠0 . Следовательно,
для сбалансированной функции n-кубитовый регистр будет находиться в состояниях, отвечающих ненулевым значениям тех или
иных битов. Состояние 00…0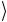 строго отсутствует.
строго отсутствует.
Итак, к квантовому «оракулу» можно обратиться один раз и, получив результат, узнать глобальное свойство функции f . Инте-
ресно сравнить с классической ситуацией. Если на входе и выходе мы имеем дело с классическими битами, то надо обращаться к
«оракулу», выбирая раз за разом какие-то числа от 0 до 2n −1, и сравнивать получающиеся результаты. Если очередной ответ отличается от предыдущего, то функция, очевидно, сбалансированная. Чтобы быть уверенным, что функция постоянная, надо получить подряд 2n-1+1 раз одинаковый результат, т.е. такое число случаев, которое на единицу больше половины. В этом смысле можно сказать, что при больших n классическое вычисление требует экспоненциально большого числа обращений к вычислителю. Поскольку в квантовом случае нужно только одно обращение, можно говорить об экспоненциальном увеличении скорости вычислений. Обратим внимание еще на один важный момент. Результат квантового вычисления (3.11) формируется благодаря эффекту интерферен-
220


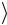 системы
системы