
Кулик Введение в теорию квантовых вычислений Книга 2 2008
.pdf
2.3.Многокубитовый регистр
Вэтом разделе мы рассмотрим квантовую систему, состоящую из n кубитов. Такую систему называют n-кубитовым регистром. Обсудим пространство состояний многокубитового квантового регистра и линейные операторы, действующие в этом пространстве, а также методы описания состояний и операторов.
Базисные векторы n-кубитовой системы строятся как произведения n штук базисных векторов отдельных кубитов
Cn-1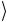
 Cn-2
Cn-2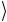 … C1
… C1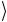
 C0
C0 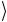 ≡ Cn-1 Cn-2 …C1 C0
≡ Cn-1 Cn-2 …C1 C0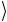 . (2.108)
. (2.108)
Здесь каждая из величин Ci принимает одно из двух значений, 0 или 1, так что символом Ci 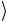 представлены базисные векторы от-
представлены базисные векторы от-
дельного кубита. Строго говоря, стоящее слева произведение однокубитовых векторов состояний представляет собой так называемое тензорное (или прямое) произведение1. Мы, однако, не будем использовать никаких специальных обозначений для такого тензорного произведения, а будем просто писать кэт-векторы однокубитовых состояний рядом как сомножители и называть такое состояние факторизованным. Заметим, что в предыдущем разделе такая запись была использована в формуле (2.19) для вектора состояния фотона как произведения соответствующих кэт-векторов, относящихся к пространственным и поляризационным степеням
1 Если вектор |α> принадлежит гильбертову пространству H1 c размерностью d1, а вектор |β> — гильбертову пространству H2 с размерностью d2 ,
то вектор |α> |β> ≡ |α>|β>, являющийся тензорным произведением векторов, принадлежит гильбертову пространству Н= H1 H2 с размерностью d= d1 d2 , которое называют тензорным произведением пространств H1 и H2. Размерность пространства каждого из кубитов равна 2. Поэтому вектор состояния |α> |β> ≡ |α>|β> двухкубитовой системы принадлежит пространству с размерностью 2·2=4. Тензорное произведение пространств и тензорное произведение векторов сохраняет фундаментальный физический принцип суперпозиции (или, говоря математическим языком, линейную структуру пространства) при переходе к пространствам большей размерности.
111

свободы. Произведение однокубитовых базисных векторов мы будем писать также в виде одного вектора состояния, обозначенно-
го скобкой ... , внутри которой стоит, как это написано в правой
, внутри которой стоит, как это написано в правой
части (2.108), цепочка двоичных символов. В дальнейшем для определенности будем считать, что в произведении (2.108) кубиты расположены (перенумерованы) слева направо.
Поскольку каждый из кубитов имеет два базисных состояния (Сi=0, 1), то n-кубитовый регистр (i=0, 1,…, n–1) имеет 2n базисных векторов, т.е. размерность пространства квантовых состояний n-кубитовой системы равна 2n. Ниже мы увидим, что именно с этим простым, по сути, фактом связана экспоненциально большая информационная емкость квантового регистра, если он содержит достаточно большое число кубитов, n >>1.
Обозначающая базисный вектор (2.108) цепочка
(Cn-1 Cn-2 … C1 C0),
состоящая из нулей и единиц, идентифицируется как двоичная запись некоторого целого числа S:
S = Cn-1 2n-1 +Cn-2 2n-2 +…+C1 21+C0 20 , (2.109)
находящегося в пределах от 0 до 2n-1. Сам базисный вектор тоже можно для краткости обозначить как
Cn-1 Cn-2 …C1 C0 = |
|
S |
(2.110) |
|
и считать, что базисные векторы перенумерованы с помощью этого числа, т.е. их последовательность выглядит так: | 00...00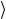 , | 00...01
, | 00...01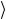 ,
,
|11...11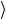 .
.
Отметим также, что отдельные кубиты в базисных состояниях (2.110) многокубитового регистра считаются перенумерованными слева направо, так что первый кубит соответствует наибольшему двоичному разряду, а последний – наименьшему.
На квантовых схемах мы будем располагать линии отдельных кубитов сверху вниз в том же порядке, как это показано на рис. 2.8.
112

Рис. 2.8
Совокупность базисных векторов (2.110) является полной ортонормированной системой, т.е. они удовлетворяют условиям нормировки, ортогональности и полноты:
S' |
S = δ s`s , |
(2.111) |
2n −1
∑ S S =1 . (2.112)
s=0
Этот набор состояний используется в качестве вычислительного базиса. На основании принципа суперпозиции произвольное со-
стояние ψ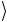 рассматриваемого n-кубитового регистра имеет вид
рассматриваемого n-кубитового регистра имеет вид
ψ = a0 0…00
= a0 0…00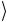 + a1 0…01
+ a1 0…01 +…+ a2n -2 1…10
+…+ a2n -2 1…10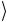 + a2n -1 1…11
+ a2n -1 1…11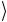 ≡
≡
2n −1 |
|
≡ ∑as | S . |
(2.113) |
s=0
Это означает, что с помощью такой квантовой системы можно одновременно записать 2n различных чисел S от 0 до 2n–1. В этом смысле можно говорить об экспоненциально большой информационной емкости квантового регистра, содержащего достаточно
113

большое число кубитов1. Еще раз обратим внимание, что, как и в случае одного кубита, состояния вычислительного базиса входят в (2.113) в виде когерентной суперпозиции, комплексные коэффициенты которой определяют не только меру (вероятность) присутствия в квантовом состоянии кубита каждого из базисных векторов, представляющих двоичные числа, но и фазовые соотношения между ними.
Рассмотрим для примера систему, состоящую из двух кубитов. Она имеет 4 базисных состояния
00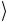 = 0
= 0
 0
0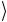 , 01
, 01 = 0
= 0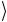
 1
1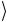 , 10
, 10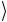 = 1
= 1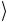
 0
0 , 11
, 11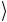 = 1
= 1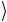
 1
1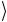 , (2.114)
, (2.114)
представляющих в двоичной записи числа 0, 1, 2 и 3, соответственно. Данная двухкубитовая система может находиться, например, в состоянии
ψ = 12 { |
|
00 + |
|
01 + |
|
10 + |
|
11 }, |
(2.115) |
|
|
|
|
||||||
|
|
|
|
|
в котором все указанные числа оказываются представленными в виде однородной и синфазной суперпозиции.
Состояние ψ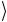 полностью определяется совокупностью 2n ком-
полностью определяется совокупностью 2n ком-
плексных чисел a0, a1, a2, …, a2n-1, которые стоят в виде коэффициентов при базисных векторах. Эти числа представляют собой скалярные произведения2
as = S |
|
ψ , S = 0, 1,…, 2n–1. |
(2.116) |
|
1Пусть n = 500, т.е. имеется регистр, содержащий 500 кубитов. В нем можно записать сразу 2500 чисел, а это больше, чем число атомов во Вселенной.
2Напомним, что скалярное произведение двух векторов |Ψ1> и |Ψ2> в гильбертовом пространстве состояний квантовой системы определяется
как комплексное число <Ψ2|Ψ1>, удовлетворяющее условию, что <Ψ1|Ψ2>=<Ψ2|Ψ1>*. Это гарантирует, что квадрат нормы любого вектора состояния |Ψ>, т.е. скалярное произведение <Ψ|Ψ> строго больше нуля. О скалярных произведениях (2.116) можно говорить как о проекциях вектора |Ψ> на базисные векторы |S>.
114
Они занумерованы с помощью индекса, совпадающего со значением (2.109) числа S, двоичная запись которого представлена цепоч-
кой из нулей и единиц, написанной внутри скобок ... , обозна-
, обозна-
чающих базисные кэт-векторы. Комплексные числа as в суперпозициях вида (2.113) могут быть произвольными.
Единственное ограничение связано с условием нормировки
ψ |
ψ = 1 |
(2.117) |
состояния ψ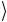 , которое эквивалентно соотношению
, которое эквивалентно соотношению
2n −1 |
|
|
∑|as|2 |
= 1. |
(2.118) |
s=0
Действительно, подставляя условие полноты (2.112) в левую часть
(2.117), получаем
|
|
|
|
2n −1 |
|
|
|
|
|
|
|
2n −1 |
||||||||
ψ |
|
ψ = ψ |
|
∑ |
|
S S |
|
ψ = |
∑ |
ψ |
|
S S |
|
ψ = |
||||||
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
s=0 |
|
|
|
|
|
|
|
|
s=0 |
|
|
|
|
|
||
|
|
2n −1 |
|
|
|
|
|
|
|
2n −1 |
|
|
|
|
|
|
||||
|
|
= ∑ |
|
|
S |
|
ψ |
|
2 |
|
= ∑|as| 2 = 1. |
|||||||||
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|||||||||||||||||
|
|
s=0 |
|
|
|
|
|
|
|
|
|
s=0 |
|
|
|
|
|
|
||
Здесь при вычислениях мы воспользовались выражением (2.116) для коэффициентов аs и свойством скалярного произведения
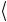 ψ S
ψ S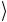 =
= 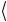 S ψ
S ψ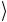 *= аs* .
*= аs* .
Итак, в базисе (2.110) любое состояние | ψ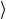 взаимно однозначно задается совокупностью коэффициентов разложения {аs}, которые,
взаимно однозначно задается совокупностью коэффициентов разложения {аs}, которые,
115

тем самым, можно использовать для описания состояния | ψ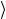 . Этот
. Этот
набор комплексных чисел мы будем писать в виде 2n — компонентного вектор-столбца
|
|
a0 |
|
|
|
|
|
|
|
|
|
|
|
| ψ |
= |
a1 |
|
, |
(2.119) |
|
... |
|
|||||
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a2n −1 |
|
|
|
расположив его компоненты в порядке возрастания индекса сверху вниз.
Теперь перейдем к рассмотрению линейных операторов, действующих в гильбертовом пространстве состояний n-кубитового
регистра. Пусть в результате действия оператора ˆ на состояние
F
| ψ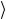 получаем состояние Φ
получаем состояние Φ , т.е.
, т.е.
ˆ |
= |
Φ . |
(2.120) |
F | ψ |
Представим векторы | ψ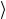 и Φ
и Φ в виде разложений по базисным состояниям S
в виде разложений по базисным состояниям S :
:
| ψ = ∑as' |
|
S' , |
|
Φ = ∑bs |
|
S . |
(2.121) |
|
|
|
|||||
s' |
|
s |
|
||||
Подставляем эти разложения в (2.120) и, учитывая линейность опе-
ратора ˆ , имеем
F
|
Φ = ∑bs |
|
S |
ˆ |
∑as' |
|
|
ˆ |
|
S' , |
||||
|
|
|
|
|
||||||||||
|
|
= F |
|
S' = ∑as' F |
|
|||||||||
|
s |
|
s' |
|
s' |
|||||||||
т.е. |
|
|
|
|
|
|
|
|
|
|||||
|
∑bs |
|
S |
|
ˆ |
|
S' |
. |
(2.122) |
|||||
|
|
|
|
|||||||||||
|
|
= ∑as' F |
|
|||||||||||
|
s |
s' |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
116 |
|
|
|
|
|
|
|
|

Проектируя обе части (2.122) на базисные векторы S с учетом условия ортонормированности (2.111), получаем
с учетом условия ортонормированности (2.111), получаем
bs = ∑ S |
|
ˆ |
|
S' as' = ∑Fss'as ' , |
(2.123) |
|
|
||||
|
F |
|
|||
s' |
|
|
|
s ' |
|
где s, s’ = 0, 1,…, 2n–1. Совокупность 2n ×2n комплексных чисел
ˆ |
(2.124) |
Fss’ ≡ S F S' , |
которые называются матричными элементами оператора ˆ в ба-
F
зисе {S }, образуют матрицу
}, образуют матрицу
|
|
F 00 |
F 01 ... |
F |
|
n |
|
|
|
|
|||
|
|
|
|
|
|
|
0,2 |
|
−1 |
|
|
||
ˆ |
|
F10 |
... ... |
F1,2n −1 |
|
(2.125) |
|||||||
F = |
|
|
... |
... Fss ' |
|
|
... |
|
|
. |
|||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
n |
− 1, 0 ... ... |
F 2 |
n |
|
|
|
n |
|
|
|
|
F 2 |
|
|
− 1, 2 |
|
− 1 |
|
||||||
Первый индекс матричного элемента — номер строки, а второй — номер столбца. Компактная алгебраическая запись (2.123) показывает, что вектор-столбец {bs}, описывающий состояние
Φˆ
=F | ψ , получается из вектор-столбца {as}, описывающего состояние | ψ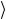 , как результат умножения слева (по стандартным
, как результат умножения слева (по стандартным
правила матричной алгебры) на матрицу Fss’, которая соответствует
линейному оператору ˆ , т.е.
F
b0 |
|
|
|
|
|
F 00 |
F 01 ... |
F0,2n −1 |
|
a0 |
|
|
|
||||
|
|
|
|
|
|
F10 |
... |
... |
F1,2n −1 |
|
|
a1 |
|
|
|
||
b1 |
|
|
|
= |
|
|
|
|
|
. (2.126) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
... |
... |
Fss ' |
|
... |
|
... |
|
|
|
|||||
... |
|
|
|
|
|
n |
n |
|
|
|
|||||||
|
n |
|
|
|
|
n |
|
|
|
|
|
|
n |
|
|
||
b2 |
− 1 |
|
|
F 2 − 1, 0 ... |
... |
F 2 |
− 1, 2 |
|
− 1 |
a2 |
− 1 |
|
|||||
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
117 |
|
|
|
|
|
|
|
|
|
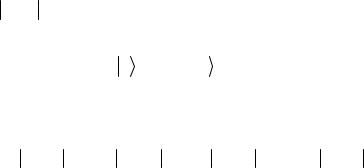
Представление, которое описывается соотношениями (2.119), (2.123)-(2.126), называется матричным представлением. В дальнейшем мы будем применять его, используя, как правило, ком-
пактные формулы вида (2.116), (2.121), (2.123), (2.124).
Что касается “многоэтажных” конструкций типа (2.126), то мы иногда будем прибегать к ним, иллюстрируя вид матриц тех или иных операторов, действующих в пространстве состояний небольшого числа кубитов.
Тензорное произведение
Мы уже говорили, что с помощью тензорного произведения пространств меньшей размерности можно построить пространство большей размерности.
Рассмотрим для примера пространство состояний 2-кубитовой системы, которое есть тензорное произведение (его называют также прямым произведением) Н2= H1 H1 пространств состояний двух однокубитовых систем, и продемонстрируем правила вычисления тензорного произведения двух однокубитовых векторстолбцов, а также матриц операторов, действующих на состояния отдельных кубитов.
Вектор-столбцы, соответствующие базисным состояниям 0 и 1
и 1 каждого кубита, имеют вид
каждого кубита, имеют вид
0 |
|
1 |
|
, |
|
1 |
|
0 |
|
(2.127) |
= |
0 |
|
|
= |
1 |
. |
||||
|
|
|
|
|
|
|
|
|
Полному набору базисных состояний 2-кубитовой системы
00 = 0
= 0
 0
0 , 01
, 01 = 0
= 0
 1
1 , 10
, 10 = 1
= 1
 0
0 и 11
и 11 = 1
= 1
 1
1 ,
,
которые строятся как тензорные произведения базисных векторов каждого из кубитов, отвечают, в соответствии с общими формулами (2.113) и (2.119) перехода к спинорному представлению,
118
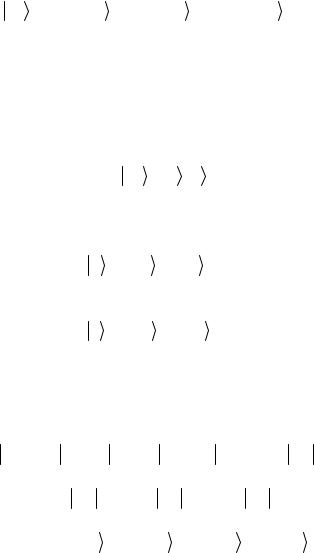
4-компонентные вектор-столбцы
|
1 |
|
|
|
0 |
|
|
|
0 |
|
|
|
0 |
|
||||
|
0 |
|
|
|
|
1 |
|
|
|
|
0 |
|
|
|
|
0 |
|
|
00 = |
|
, |
|
01 = |
|
, |
|
10 = |
|
и |
|
11 = |
|
. (2.128) |
||||
|
|
|
||||||||||||||||
|
0 |
|
|
|
|
0 |
|
|
|
|
1 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
||||||||||||
|
0 |
|
|
|
|
0 |
|
|
|
|
0 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Поэтому эти вектор-столбцы являются тензорными произведениями однокубитовых вектор-столбцов (2.127). Чтобы понять правило вычисления тензорного произведения вектор-столбцов, рассмотрим вектор состояния 2-кубитовой системы
ab = |
|
a 1 |
|
b 2 , |
(2.129) |
|
|
|
который есть произведение векторов состояний
a |
|
0 |
|
|
|
|
a0 |
|
|
|
1 = a0 |
1 + a1 |
1 1 |
= |
1 |
, |
|
||||
|
|
|
|
|
|
|
a1 |
|
(2.130) |
|
|
|
|
|
|
|
|
b0 |
|
||
b |
|
0 |
|
|
|
|
|
|
||
2 = b0 |
2 + b1 |
1 |
2 |
= |
|
|
2 |
|||
|
|
|
|
|
|
|
b1 |
|
|
|
двух кубитов, отмеченных индексами 1 и 2. Подставляем (2.130) в (2.129) и перемножаем почленно, располагая кубиты в порядке нумерации слева направо. Тогда
ab = (a0 0
= (a0 0 1 + a1 1
1 + a1 1 1 )( b0 0
1 )( b0 0 2 + b1 1
2 + b1 1 2 ) = a0b0 0
2 ) = a0b0 0 1 0
1 0 2 +
2 +
+a0b1 0 1 1
1 1 2 + a1b0 1
2 + a1b0 1 1 0
1 0 2 + a1b1 1
2 + a1b1 1 1 1
1 1 2 =
2 =
=a0b0 |
00 + a0b1 |
01 + a1b0 |
10 + a1b1 |
11 . |
(2.131) |
119 |
|
|
|
||
Из этого разложения видно, что вектор-столбец двухкубитовой системы получается из вектор-столбцов (2.130) c помощью равенства
|
|
|
|
|
|
|
|
|
a0 b0 |
|
b0 |
|
|
||||
a |
0 |
|
|
b |
0 |
|
|
|
|
a |
0 1 |
|
a0 |
b1 |
|
|
|
|
|
|
|
= |
|
b |
= |
|
|
|
. |
(2.132) |
|||||
|
|
|
1 |
|
|
|
2 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
a1 b0 |
|
|
b0 |
|
|
|||
a1 |
|
|
b1 |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
a1 b1 |
|
|
1 |
|
|
|
||
|
|
|
|
|
|
|
|
|
a1 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
На последнем шаге в (2.132) 4-компонентный вектор-столбец специально записан в такой форме, что процедура вычисления выглядит вполне очевидной. Обратим также внимание, что результирующий вектор-столбец в (2.132), т.е. расположение его компонент, зависит от порядка сомножителей. Соблюдение такого порядка расположения однокубитовых вектор-столбцов, когда на первом месте стоит первый кубит, на втором месте – второй кубит и так далее, позволяет сохранить единую нумерацию базисных векторов (2.110) и, соответственно, компонент спинора (2.119). Сформулированное правило вычисления тензорного произведения, которое называют также кронекеровым произведением, очевидным образом обобщается на произведение любого числа любых векторстолбцов. В качестве иллюстрации можно проверить, что вычисленные с помощью формулы (2.132) тензорные произведения век- тор-столбцов (2.127), отвечающих однокубитовым базисным состояниям, действительно дают вектор-столбцы (2.128), которые описывают базисные состояния двухкубитовой системы.
Теперь рассмотрим правило вычисления кронекерова произведения матриц. Пусть на состояние (2.129) двухкубитовой системы
ˆ ˆ = ˆ ˆ
действует линейный оператор F G FG , представляющий собой произведение двух операторов. При этом каждый из операторов действует на состояние только одного из кубитов. Для опреде-
ленности считаем, |
|
|
ˆ |
действует |
|
|
|
|
|
ˆ |
|||
|
|
|
|
|
|||||||||
что F |
на |
|
|
|
a 1 , а G действует на |
||||||||
|
b 2 следующим образом: |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
b 2). |
|
||||
|
|
|
|
|
|
|
|
|
|||||
|
ˆ |
ˆ |
|
ab |
ˆ |
|
|
ˆ |
|
(2.133) |
|||
|
|
|
|
||||||||||
|
(F G) |
|
= (F |
|
a 1) (G |
|
|||||||
|
|
|
|
|
120 |
|
|
|
|
|
|
||
