Кулик Введение в теорию квантовых вычислений Книга 2 2008

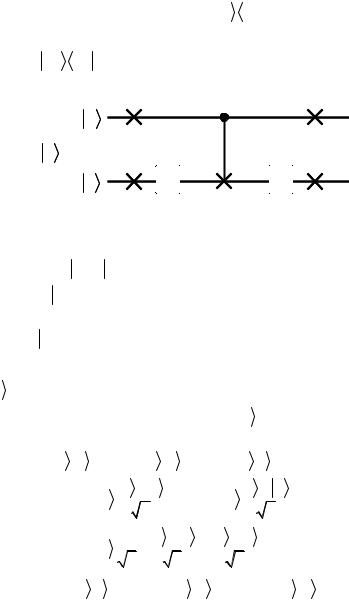
В нашем случае двухкубитового регистра данных оператор (3.53) выглядит следующим образом:

	(			)
U s = H 2		2	00	00	−1 H 2 .	(3.55)

На рис. 3.7 показана квантовая схема, реализующая действие опе-

ратора 2 00	00 −1 условного фазового сдвига, стоящего в круг-
лых скобках в выражении (3.55).
		a
x
		b	H	H

Рис. 3.7 Чтобы убедиться в этом, посмотрим, как преобразуются базис-

ные векторы x = a b двухкубитового регистра. Если на входе состояние 1 b , то операция CNOT на второй кубит не действует, так как после операции NOT над первым кубитом получается состояние 0 b . Поэтому второй кубит подвергается преобразованию σ1HHσ1 =1, т.е. не меняется. Итак, для любого b состояние

1b не меняется.

00 .

Пусть теперь на входе состояние

Тогда последователь-

ность преобразований выглядит так

0

0 → 1

0 → 1 1 →

NOT1

NOT2

H2

→ 1

→ 1

2

→

2

H

2

0 −

1

CNOT

1 − 0

H2

H

1

1

0

−

1

−

0

+

1

=

→

2

2

2

2

= − 1 1

0 .

→− 1

0 →− 0

NOT2

NOT1

241

Для аккуратности заметим, что индексы 1 и 2 показывают, на какой кубит действует операция, написанная над стрелкой. Итак,

00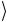→ − 00 .

Наконец, начальное состояние 01 преобразуется следующим образом:

01→NOT1 11→NOT2 1 0→H2

→ 1							2						→								1						2	→
	H2					0	+			1							CNOT								1	+ 0		H2
	H2				1						0			−			1			0 +				1
→				1	2									2				+			2						=
= 1 0																											1 ,
				→ 1											1 → 0
					NOT2													NOT1

т.е. это состояние не меняется, как и все состояния вида 1b . В

результате получаем, что фаза состояний 01 , 10 и 11 поме-

нялась на противоположную относительно фазы состояния 00 .

Собирая все фрагменты (3.4) – (3.7) конструкции, получаем окончательный вид квантовой схемы, описывающей одну итерацию алгоритма Гровера, осуществляющего поиск в базе данных из 4-х элементов:

Рис. 3.8

242

Для наглядности пунктирным прямоугольником выделен блок, описывающий оператор 2 0000 −1 условного фазового сдвига, схема которого представлена на рис. 3.7. Этот блок взят в «обклад-

ки» из оператора H 2 , чтобы получить преобразование (3.55) инверсии относительно среднего.

Операторы H и σ1 , стоящие справа на линии вспомогательного кубита, возвращают его в начальное состояние 0 .

Квантовый поиск в базе данных из 4-х элементов представляет собой некоторый забавный специальный случай. Если N = 4 , то из

общих формул (3.45) и (3.49) следует, что sin θ =1 N =12 , т.е.

θ = π6 , а θ1 = 3θ = π2 . Тогда, согласно (3.50), амплитуда β1 иско-

мого состояния после первой итерации Гровера (k=1)

β1 = sin 3θ =1

оказывается максимально возможной, т.е. одна итерация Гровера с достоверностью дает искомое число.

Взаключение отметим несколько важных моментов, связанных

сзадачей поиска. Можно показать, что алгоритм квантового поиска Гровера, который решает задачу с использованием только по-

рядка N обращений к «оракулу», является оптимальным, и решить задачу за меньшее число шагов нельзя.

Абстрактная задача поиска относится к числу фундаментальных математических проблем. Это не только поиск в той или иной базе данных, но и определение, например, количества решений, так называемых, трудных задач, которые могут быть сформулированы как вопрос о существовании решения задачи поиска.

Квантовый алгоритм Гровера показывает, что процедуру поиска можно заметно ускорить по сравнению с расчетами на классическом компьютере.

243

Задачи

1. Вычислить число шагов, которое требуется, чтобы найти один элемент в неупорядоченной базе данных, содержащей N элементов.

Решение

Вероятность найти нужный элемент на первом шаге есть W1 = 1/N. Вероятность найти на втором шаге есть произведение вероятности 1 – W1 отрицательного исхода первого шага и вероятности 1/(N – 1) удачного исхода второго шага, т.е.

W2 = (1–1/N) /(N – 1) = 1/N. Вероятность найти на третьем шаге есть

W3 = (1–2/N) / (N – 2) = 1/N,

где (1–2/N) есть вероятность отрицательного исхода на двух первых шагах. И так далее. Тогда общая формула для вероятности найти искомый элемент ровно на S-ом шаге есть WS = 1/N. Среднее число шагов есть

	N	N (N +1)		N		1		N
	S = ∑SWS =		=		+		≈		при N >> 1.
		2N		2		2		2
	S =1

Если точно известно, что в базе данных есть искомый элемент, то последний N-й шаг делать не надо, и S надо уменьшить на величину 1/N.

2. Дать «геометрическую» интерпретацию унитарного преобразо-

вания (3.20)

Решение
Пусть		ω — некоторый	базисный вектор состояния n-
кубитового регистра. Действие унитарного оператора
		ˆ	− 2		ω ω
		Uω =1

N −1

на произвольное нормированное состояние ψ = ∑ax x

x=0

244

системы, где N = 2n, имеет вид

ˆ

ψ

= ∑ax

x −aω

ω ≡

Φ .

Uω

x≠ω

Представим состояние

ψ в виде суммы

| ψ = ∑ax

x −aω

ω = 1−

aω

2

Ω + aω

ω ,

x≠ω

где кэт-вектор

ax

Ω = ∑

x

1−

aω

2

x≠ω

нормирован на

единицу и

ортогонален вектору

ω , т.е.

Ω

Ω = ω

ω =1,

Ω

ω = 0 . Тогда для преобразованного со-

стояния имеем

Φ

ˆ

ψ =

1−

aω

2

Ω − aω

ω .

=Uω

Без ущерба для общности можно считать, что коэффициент aω — действительный. Тогда

ψ =cos θ Ω + sin θ ω,

Φ = cos θ Ω ─ sin θ ω,

где tg θ=		aω		. Представив		Ω и			ω как “орты” двумерной
		1− aω	2
								Φ как векторы, которые
системы	координат, изобразим				| ψ и
			245

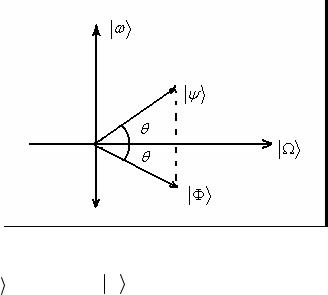
показаны на следующем рисунке:

Таким образом, преобразование ˆω представляет собой “отраже-

U

ние” | ψ относительно Ω .

3.3. Квантовый алгоритм Шора

Важной вехой в становлении квантовой информатики явилось открытие в 1994 г. Питером Шором квантового алгоритма для эффективной факторизации больших чисел. Этот результат привлек внимание широкой научной общественности потому, что проблема факторизации, которая известна каждому, кто познакомился с началами арифметики, выступает как своего рода «жупел» для вычислительной математики. Считается, хотя это и не доказано, что для больших чисел эта задача является трудной с точки зрения теории вычислительной сложности. Немаловажную роль сыграл и тот факт, что именно трудность факторизации лежит в основе защищенности наиболее надежных на сегодняшний день методов криптографии. Возможность практического решения проблемы факторизации больших чисел выступает как демонстрация потенциальной мощи использования квантовых явлений для выполнения вычислений.

Изложение основного материала этого раздела предваряется

246

очень кратким качественным обзором некоторых вопросов, составляющих предмет формальной математической теории вычислительной сложности. Цель состоит в том, чтобы пояснить содержание таких понятий как «трудная задача» или «эффективный метод решения». Далее излагается дискретное квантовое преобразование Фурье (КПФ), которое играет ключевую роль в целом ряде квантовых алгоритмов, в том числе, в алгоритме Шора. Проводится сопоставление КПФ с классическим аналогом, так называемым быстрым преобразованием Фурье. Описывается квантовая схема, реализующая КПФ. Наконец, излагается идея алгоритма Шора.

В основе лежит тот факт, что проблема факторизации обладает важной структурой, которая позволяет свести процедуру построения решения к поиску периода длинной последовательности. Показывается, что квантовый алгоритм Шора эффективно решает эту задачу с экспоненциальным ускорением по сравнению с известными классическими алгоритмами.

Понятие вычислительной сложности

К понятию вычислительной сложности теория подходит, основываясь на том, какие ресурсы времени и памяти требуются для того или иного вычисления. Во главу угла ставится не столько сам факт существования или отсутствия алгоритма вычисления, сколько существование эффективного алгоритма. Это понятие можно формализовать (см. книгу 1), как это делается в теории вычислительной сложности, выделяя классы тех функций (или предикатов), вычисление которых возможно при задаваемых ограничениях на потребляемые ресурсы. Соответствующие совокупности называются классами сложности.

Такая характеристика функции как принадлежность к тому или иному классу сложности должна определять возможности ее вычисления, не связанные с конкретными реализациями алгоритмов.

Наиболее существенное различие между классами определяется ограничениями, которые накладываются на рост временных затрат, или объема памяти, или того и другого в зависимости от длины входного слова, т.е. от длины n двоичной строки, подаваемой на вход. Разграничение между эффективными и неэффективными

247

f (n)

вычислениями задается функциями полиномиального роста1. Задача считается легкой или решаемой, если для ее решения

существует алгоритм, требующий ресурсов, ограниченных функцией poly(n). В этом случае говорится, что есть эффективный алгоритм решения.

Рост быстрее любой степени принято называть экспоненциальным, хотя это может быть, например, функция типа

exp (log n)2 = nlog n , которая растет быстрее любого многочлена,

но медленнее, скажем, экспоненты exp (nα ) с 0 < α <1. Задача

считается трудной или нерешаемой, если любой возможный алгоритм требует экспоненциального ресурса. В этом случае считается, что нет эффективного алгоритма решения.

Разделение эффективных и неэффективных алгоритмов с помощью функций полиномиального роста не зависит от выбора модели вычислений. Это утверждение связано с так называемым тезисом Чёрча-Тьюринга, суть которого в несколько упрощенной форме сводится к тому, что различные модели вычислений отличаются только полиномиальным изменением числа операций. Поэтому принадлежность алгоритма полиномиальному или экспоненциальному классам не зависит от модели вычислений.

Мы не будем дальше погружаться в формальную математическую теорию вычислительной сложности. Главная цель предыдущего обсуждения состояла в том, чтобы пояснить, почему разграничение между эффективными и неэффективными вычислениями, т.е. между наиболее важными классами сложности, определяется полиномиальной либо экспоненциальной зависимостью ресурса от размера входных данных. Другими словами, вычислительная сложность определяется числом шагов (элементарных логических гейтов) S, которое необходимо, чтобы с помощью наилучшего из известных алгоритмов решить задачу, т.е. по информации, заданной на входе, получить результат на выходе. Пусть количество

1 Функция называется функцией полиномиального роста, если при достаточно больших n выполняется неравенство f (n) ≤ nα с некоторой константой α > 0 . Такая функция обозначается как f (n) ≡ poly(n).

248

информации, т.е. число битов, необходимое для ее хранения, есть n. Так, для числа M эта величина есть n log2 M . Считается, что задача поддается вычислению, если S(n) = poly(n) . Такая задача

относится к классу сложности P (от слова polynomial). Существуют задачи, неразрешимые за полиномиальное время. Вспомним уже известную нам проблему поиска в неупорядоченной базе данных

из 2n элементов, когда число шагов любого классического алгоритма просто пропорционально размеру базы, т.е. зависит от n экспоненциально. Кстати, квантовый поиск тоже требует экспоненциального ресурса. Можно привести целый ряд примеров таких задач, для которых полиномиальные алгоритмы неизвестны, хотя в каждом конкретном случае доказательство того, что данная проблема неразрешима за полиномиальное время и требует экспоненциального ресурса, может отсутствовать.

Важным примером такой задачи, для которой не известен простой метод решения, является проблема факторизации, т.е. разложения большого числа на множители. Принято считать, что она не принадлежит классу P. Примечательным свойством этой задачи и целого ряда других задач является то, что истинность того или иного предъявленного решения можно легко проверить за полиномиальное число шагов. Эти задачи принадлежат к классу сложно-

сти NP (от слов nondeterministic polynomial). Пока остается нере-

шенной одна из фундаментальных проблем теории сложности – есть ли NP-задачи, не принадлежащие к классу P.

Наилучший известный классический алгоритм факторизации числа M 1 – «решето числового поля» – требует экспоненциально большого числа шагов

S exp (8 3)2 3	(ln M )1 3 (ln ln M )2 3 .	(3.56)

Можно оценить, что для факторизации числа, содержащего, скажем, 130 десятичных знаков, потребуется порядка 1018 шагов. При

быстродействии 1012 с−1 вычисление займет 12 дней. Кстати, в 1994 г. факторизацией 129-значного числа, известного как RSA 129, были заняты более полутора тысяч рабочих станций в течение 8

249

месяцев. Если увеличить число до 250 десятичных знаков, то при

быстродействии 1012 с−1 для его факторизации понадобится несколько тысячелетий. Эти оценки дают представление о том, что такое трудная задача.

Заметим, что практическая значимость этой теоретико-числовой задачи связана с тем, что сложность разложения на множители определяет защиту и секретность широко распространенных криптографических систем.

Например, известная криптографическая система с открытым ключом RSA, разработанная в 1979 г. Роном Ривестом, Ади Шамиром и Леонардом Адлеманом, использует следующую процедуру. Пусть большое число c = p q есть произведение двух больших

простых чисел p и q. Боб шифрует текст сообщения T с помощью некоторого нечетного числа t, которое является взаимно простым с

числом φ(c) = (p −1)(q −1), которое представляет собой так называемую функцию Эйлера. Для этого он вычисляет величину1

M (T ) =T t (mod c)

(3.57)

и посылает ее Алисе. Получив от Боба послание M (T ) , Алиса

расшифровывает его с помощью числа m, которое находит из условия

m t =1(mod φ(c)).	(3.58)
Для дешифровки Алисе достаточно	вычислить величину

(M (T ))m (mod c). Можно показать (см. задачу 1 в конце этого раздела), что эта величина в точности совпадает с текстом,

1 Соотношение a = b(mod c) эквивалентно равенству a = k c +b , где все буквы обозначают целые неотрицательные числа, и b < c .

250