
Кулик Введение в теорию квантовых вычислений Книга 2 2008
.pdf
На последнем шаге для полноты картины использовано спинорное представление.
Вид выражения (2.164), которое описывает максимально перепутанное состояние Ψ(−) 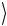 , не меняется при переходе к другому
, не меняется при переходе к другому
базису одночастичных спиновых состояний. Покажем это, например, для базиса состояний с определенными проекциями спина на
ось x. Собственные состояния оператора sˆx , отвечающие собственным значениям sx = ±1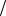 2 , имеют следующий вид:
2 , имеют следующий вид:
sx =1 2 = |
1 |
1 |
, |
|
sx = −1 2 = |
1 |
|
1 |
. (2.165) |
|
|
|
|
|
|||||||
|
|
|||||||||
|
2 |
1 |
|
|
|
2 |
|
−1 |
|
Раскладывая по этим состояниям спиноры, которые входят в выражение (2.164), получаем:
|
(−) |
|
|
|
|
|
|
|
1 |
|
1 |
|
|
|
1 |
|
|
1 |
|
|
1 |
|
|
1 |
|
|
|
|
|||||||
Ψ |
= |
|
|
1 |
|
|
+ |
|
|
|
|
− |
|
−(1 2) |
|
= |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
2 |
|
1 |
|
|
−1 |
|
|
2 |
|
|
1 |
2 |
|
−1 |
2 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
1 |
|
1 |
1 |
1 |
|
|
1 |
1 1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
= − |
|
|
|
− |
|
|
= |
|
|
|
|
|
|
|
(2.166) |
||||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
1 −1 |
2 |
|
−1 1 |
2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
= − |
|
1 |
{ |
|
sx =1 2 1 |
|
sx = −1 2 2 − |
|
sx = −1 2 1 |
|
sx =1 2 2}. |
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
2 |
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Мы видим, что Ψ(−) 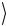 остается максимально перепутанным со-
остается максимально перепутанным со-
стоянием, антисимметричным относительно перестановки частиц. Проекции спинов на ось x остаются жестко скоррелированными. Точно так же, как это было с проекциями спинов на ось z.
В случае произвольной оси n формальное доказательство проводится аналогичным образом с помощью разложений по собственным состояниям оператора sn проекции спина на эту ось (см.
задачу 2 в конце этого раздела). С физической точки зрения результат легко понять из следующего рассуждения. Действительно, выбор оси квантования n вместо z эквивалентен преобразованию
141

поворота системы координат, которое, как уже говорилось выше, не меняет величину суммарного спина. Поскольку в синглетном
состоянии Ψ(−) 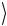 суммарный спин S = 0 , а следовательно, и его
суммарный спин S = 0 , а следовательно, и его
проекция на любую ось n тоже равна нулю, то структура выражения (2.164) остается неизменной при выборе любого базиса.
Таким образом, в состоянии Ψ(−) 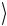 проекции спинов на любую
проекции спинов на любую
ось остаются жестко скоррелированными: если измерение одной из проекций на эту ось дает значение +1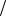 2 , то измерение другой проекции даст с достоверностью результат −1
2 , то измерение другой проекции даст с достоверностью результат −1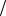 2 , и наоборот.
2 , и наоборот.
Инвариантность структуры выражения (2.164) относительно выбора базиса одночастичных спиновых состояний, т.е., фактически относительно преобразования поворота системы координат, представляет интерес для анализа свойств двухкубитовых гейтов.
При повороте системы координат состояние двухкубитовой спиновой системы преобразуется по закону (2.149), который опре-
деляется унитарным оператором вращений Φ ˆ
exp(i nS) . Этот опе-
ратор представляет собой некоторый приводимый двухкубитовый гейт, который строится как тензорное произведение двух одинако-
вых однокубитовых преобразований Φ ˆ1,2 . В результате exp(i ns )
такого преобразования состояние Ψ(−) 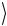 остается перепутанным
остается перепутанным
состоянием и не может быть записано в факторизованном виде. Поэтому мы приходим к выводу, что с помощью двух одинаковых
однокубитовых гейтов перепутанное состояние Ψ(−)  нельзя пре-
нельзя пре-
образовать ни в какое факторизованное состояние. В силу обратимости унитарных преобразований справедливо и обратное утверждение, что с помощью двух одинаковых однокубитовых гейтов из факторизованных двухкубитовых состояний нельзя получить пере-
путанное состояние Ψ(−)  .
.
Сформулированные утверждения можно существенно усилить.
Рассмотрим приводимый двухкубитовый гейт ˆ = ˆ1 ˆ2
U
U
U , который имеет вид тензорного произведения двух произвольных одно-
142
кубитовых преобразований. В общем случае ˆ и ˆ представля-
U1 U2
ют собой однокубитовые вращения, но вокруг разных осей и на разные углы. Напомним, что унитарные преобразования сохраняют скалярные произведения и переводят один полный набор базисных состояний в другой полный набор. Поэтому в результате действия
ˆ |
на базисные векторы |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||||||
оператора U1 |
|
±1 2 1 первого кубита |
|
|
|||||||||
|
|
|
|
|
|
|
|
||||||
|
ˆ |
|
|
|
|
|
ˆ |
|
|
|
|
(2.167) |
|
|
|
|
|
|
|
||||||||
|
U1 |
|
1 2 1 = |
|
α 1 |
, U1 |
|
−1 2 1 = |
|
β 1 |
|||
|
|
|
|
|
|
α 1 и |
|||||||
получается полный ортонормированный набор состояний |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
β 1 . Эти состояния являются линейно независимыми1. Аналогич-
1 . Эти состояния являются линейно независимыми1. Аналогич-
но, в |
результате |
действия |
|
|
ˆ |
на базисные |
векторы |
|||||||||||||||||||||||||||
оператора U2 |
||||||||||||||||||||||||||||||||||
|
|
±1 2 2 |
|
второго кубита получаем ортонормированный базис |
|
γ 2 |
||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||
и |
|
δ 2 . Эти состояния тоже линейно независимые. Тогда |
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
ˆ |
|
|
Ψ |
(−) |
= |
|
|
ˆ |
|
|
ˆ |
|
Ψ |
(−) |
= |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
U |
|
|
|
|
|
|
(U1 |
U2 ) |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
ˆ |
|
|
|
|
|
ˆ |
|
|
|
|
|
ˆ |
|
|
ˆ |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
= |
|
|
|
2 |
{(U1 |
1 2 |
1)(U2 |
|
|
|
−1 2 |
2 ) −(U1 |
|
−1 2 |
1)(U2 |
|
1 2 2 )}= |
(2.168) |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
= |
|
|
|
1 |
|
{ |
|
α |
1 |
|
δ 2 − |
|
β 1 |
|
γ 2}. |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Получившийся вектор состояния может быть записан в факторизованном виде a 1 b
1 b 2 тогда и только тогда, когда между парой век-
2 тогда и только тогда, когда между парой век-
торов α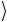 1 и β
1 и β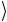 1 , либо между γ
1 , либо между γ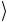 2 и δ
2 и δ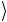 2 существует линейная зависимость.
2 существует линейная зависимость.
Линейная зависимость этих состояний означала бы, что у оператора ˆ
1 U1
есть нулевое собственное значение. У унитарного оператора таких собственных значений нет.
143

Таким образом, перепутанное состояние Ψ(−) 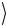 нельзя превра-
нельзя превра-
тить в факторизованное состояние с помощью одних только однокубитовых унитарных операций. Это утверждение справедливо не
только для Ψ(−) 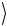 , но для всех состояний Белла (2.162) и (2.163).
, но для всех состояний Белла (2.162) и (2.163).
Дело в том, что сами состояния Белла можно получить друг из друга с помощью однокубитовых гейтов. Применяя, например, в со-
стоянии Ψ(−) 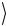 ко второму кубиту операцию σ1(2) , т.е. однокубитовый гейт NOT (2.56), получаем
ко второму кубиту операцию σ1(2) , т.е. однокубитовый гейт NOT (2.56), получаем
σ1(2) Ψ(−) 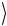 = 12 {0
= 12 {0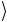 (σ1(2) 1
(σ1(2) 1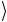 ) − 1
) − 1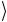 (σ1(2) 0
(σ1(2) 0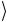 )}= (2.169)
)}= (2.169)
= 12 {00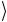 − 11
− 11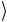 }= Φ(−)
}= Φ(−) 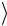 .
.
Можно написать также ряд других соотношений вида
σ3(1) |
Ψ(−) |
= |
|
Ψ(+) , |
|
|
|
|
(2.170) |
σ3(1) |
Φ(−) |
= |
Φ(+) . |
|
Если с помощью однокубитовых операций можно было бы факторизовать одно из состояний Белла, то это можно было бы сделать и для всех остальных.
Итак, для построения унитарных преобразований в пространстве двухкубитовых состояний одних только однокубитовых гейтов недостаточно. С их помощью, как мы видим, нельзя «распутать» перепутанные состояния Белла, т.е. связать их с факторизованными двухкубитовыми состояниями. Это означает, что нужны более сложные – неприводимые двухкубитовые операции.
Если на факторизованное состояние подействовать однокубитовыми операциями, то оно, конечно, останется факторизованным. При этом каждый кубит переходит, вообще говоря, в суперпози-
цию исходных базисных состояний 0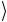 и 1
и 1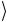 , а кэт-вектор системы
, а кэт-вектор системы
принимает форму перепутанного состояния этих базисных векторов. Это означает, что в отличие, скажем, от состояний Белла, ко-
144

торые остаются перепутанными в любом вычислительном базисе, есть множество других состояний, являющихся перепутанными в одном базисе, но факторизующихся при переходе к другому базису. Например, двухкубитовое состояние (2.115) является перепу-
танным в базисе { 0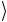 , 1
, 1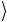 }. С другой стороны, из соотношения
}. С другой стороны, из соотношения
(2.141) следует, что оно имеет факторизованный вид в базисе состояний
|
|
0 + |
|
1 |
= |
1 |
1 |
, |
|
|
0 |
− |
|
1 |
= |
1 |
|
1 |
, |
(2.171) |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
2 |
|
2 |
|
|
|
2 |
|
2 |
||||||||||||
|
|
1 |
|
|
|
|
|
|
|
−1 |
|
|
||||||||
которые представляют собой собственные векторы (2.165) оператора проекции спина на ось x. Этим свойством обладает и n-кубитовое состояние (2.143).
Перепутанные поляризационные состояния фотонов
В задачах, связанных с передачей квантовой информации, т.е. в квантовых коммуникационных схемах, широко используются кубиты, построенные на поляризационных состояниях фотонов. Определяющую роль в этих процессах играют перепутанные поляризационные состояния.
Хотя квантовая суть явления перепутывания поляризационных состояний такая же, как для спина, сами физические системы и способы манипулирования их состоянием существенно разные. Поэтому мы остановимся более подробно на описании перепутанных поляризационных состояний.
Напомним, что два базисных состояния
|
kv ≡ |
|
v |
k и |
kh ≡ |
|
h |
k |
(2.172) |
|
|
|
|||||||
фотона характеризуются волновым вектором k |
и двумя направле- |
||||||||
ниями поляризации. Эти направления ортогональны k , и мы бу- |
|||||||||
дем называть их вертикальной (v) и горизонтальной (h) поляризациями. Кроме того, можно формально считать, что базисные век-
торы имеют факторизованный вид (2.172), в котором k относит-
относит-
145
ся к пространственным степеням свободы, а v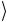 и h
и h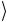 описывают поляризационную степень свободы. Поляризационные состояния отождествляются с кубитом: v
описывают поляризационную степень свободы. Поляризационные состояния отождествляются с кубитом: v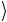 ≡ 0
≡ 0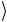 и h
и h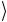 ≡ 1
≡ 1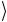 .
.
Рассмотрим систему, состоящую из двух фотонов с одинаковы-
ми волновыми векторами k , но разными поляризациями. Так как фотоны являются бозонами, то вектор состояния системы должен быть симметричным относительно операции перестановки частиц 1 и 2. Поэтому вектор состояния имеет следующий вид:
|
Ψ(1,2) |
= ( |
|
vk 1 |
|
hk 2 + |
|
hk 1 |
|
vk 2 ) 2 = |
|||||||||||||
|
|
|
|
|
|||||||||||||||||||
|
|||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||
|
|
1 |
( |
|
|
|
|
|
|
|
|
|
|
|
|
v 2 ) |
|
|
(2.173) |
||||
= |
|
v |
1 |
|
h 2 + |
|
h 1 |
|
k |
k . |
|||||||||||||
|
|
|
|
||||||||||||||||||||
2 |
|||||||||||||||||||||||
|
|
|
|
|
|
|
1 |
|
2 |
||||||||||||||
Выражение, стоящее в круглой скобке, представляет собой перепутанное поляризационное состояние, которое совпадает с симмет-
ричным состоянием Белла Ψ(+) 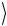 (2.164):
(2.164):
Ψ(+) = ( |
|
v 1 |
|
h 2 + |
|
h 1 |
|
v 2 ) |
2 = |
1 |
( |
|
01 + |
|
10 ). (2.174) |
|
|
|
|
|
|
||||||||||
|
|
|
|
2 |
|||||||||||
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тот факт, что получилось симметричное перепутанное поляризационное состояние, легко понять из следующих соображений. Поскольку волновые векторы одинаковые, то пространственная, т.е.
зависящая от k часть вектора состояния может быть только симметричной относительно перестановки частиц. Поэтому поляризационная часть должна быть тоже симметричной, чтобы обеспечить бозонную перестановочную симметрию вектора состояния.
Для системы двух фотонов с разными волновыми векторами можно реализовать остальные перепутанные поляризационные
состояния Белла Φ(±)  и Ψ(−)
и Ψ(−) 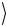 .
.
146
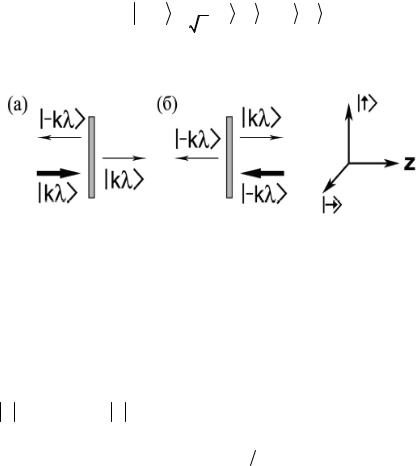
Светоделитель и измерение антисимметричного поляризационного состояния Белла
Рассмотрим простую модель светоделителя и покажем, как с помощью такой системы можно измерить одно из перепутанных поляризационных состояний Белла для двух фотонов, а именно антисимметричное состояние
Ψ(−) = |
1 |
( |
|
v 1 |
|
h 2 − |
|
h 1 |
|
v 2 ). |
(2.175) |
|
|
|
|
|
|||||||||
2 |
||||||||||||
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
Эта модель схематически изображена на рис. 2.11
Рис. 2.11
Тонкая плоскопараллельная пластина, изготовленная из диэлектрического материала и частично посеребренная с одной стороны, разделяет пространство на две части. Световое поле, падающее на эту пластину слева (а) или справа (б), с некоторыми вероятностями проходит через пластину или отражается от нее. О такой системе принято говорить, что у нее есть два входных и два выходных канала. Пусть поглощение отсутствует, а вероятности прохождения
T 2 и отражения R 2 равны, т.е.
|
T |
|
2 = |
|
R |
|
2 =1 2 . |
(2.176) |
|
|
|
|
Это светоделитель 50/50.
147
Рассмотрим поведение монохроматической моды в одномерной геометрии, когда фотоны с волновыми векторами ± k распространяются вдоль оси z. Для простоты считаем, что оба входных канала совершенно симметричны. Кроме того, предполагается, что процессы отражения и прохождения не зависят от поляризации и не меняют эту поляризацию. Два линейно независимых поляризационных состояния, отвечающие вертикальной и горизонтальной
поляризациям, обозначим как λ ≡{ v
≡{ v , h
, h }.
}.
В отсутствие светоделителя состояния ±kλ являются незави-
являются незави-
симыми. Действие светоделителя приводит к когерентному перемешиванию этих состояний. Так, падающий на светоделитель сле-
ва фотон в состоянии kλ , переходит в следующее суперпозиционное состояние (рис. 2.11а):
, переходит в следующее суперпозиционное состояние (рис. 2.11а):
ˆ |
≡ a =T kλ + R −kλ , |
(2.177) |
kλ → D kλ |
ˆ представляет собой оператор, описывающий действие свегде D
тоделителя, а T и R являются амплитудами вероятности прохождения и отражения. Аналогично, для фотона, падающего справа (рис. 2.11б), имеет место следующее преобразование:
ˆ |
≡ b =T −kλ + R kλ . (2.178) |
−kλ → D −kλ |
В преобразованиях (2.177) и (2.178) использовано в явном виде предположение, что воздействие светоделителя симметрично, сохраняет поляризацию и не зависит от нее.
Исходные состояния ±kλ образуют полный ортонормиро-
образуют полный ортонормиро-
ванный базис. Сохранение полной вероятности в отсутствие поглощения эквивалентно сохранению нормировки, т.е.
kλ |
|
kλ = |
a |
|
a = |
kλ |
|
ˆ + |
|
ˆ |
|
kλ = |
|
T |
|
2 |
+ |
|
|
R |
|
2 |
=1, |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
D D |
|
|
|
|
|
|
|
|
|
|
(2.179) |
|||||||||||||||||||||
−kλ |
|
−kλ = b |
|
b = −kλ |
|
ˆ + ˆ |
|
−kλ = |
|
T |
|
2 |
|
|
R |
|
2 |
||||||||||||||||||
|
|
|
|
|
|
+ |
|
|
=1. |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
D D |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
148 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Поскольку базис полный, то оператор
ˆ + ˆ |
(2.180) |
D D =1. |
Кроме условия (2.179) на амплитуды T и R накладывается еще одно
условие. У оператора ˆ не может быть нулевых собственных зна-
D
чений. Иначе это означало бы, что воздействие светоделителя на какое-то однофотонное состояние приводит к исчезновению этого
фотона. Поэтому оператор ˆ является обратимым, т.е. у него есть
D
обратный оператор ˆ −1 . Совместно с условием (2.180) это означа-
D
ет, что оператор ˆ является унитарным. Такой оператор сохраняет
D
скалярные произведения, и, следовательно, состояния a и b
и b ортогональны. Это дает
ортогональны. Это дает
b |
|
a = |
( |
T * |
−kλ |
|
+ R* kλ |
)( |
T |
|
kλ + R |
|
−kλ |
) |
(2.181) |
|
|
|
|
|
|
|
= |
= T *R + R*T = 0.
Без ущерба для общности можно считать, что амплитуда прохождения T действительная и неотрицательная величина. Это регулируется выбором некоторого общего фазового множителя. Тогда, учитывая (2.176), имеем
T =1 2 . |
(2.182) |
После этого из (2.181) получаем, что
R + R* = 2 Re R = 0 ,
т.е. амплитуда отражения R является величиной чисто мнимой. Принимая во внимание (2.176), ее можно положить равной
R = −i 2 . |
(2.183) |
149 |
|
Как мы увидим ниже, именно это обстоятельство формально обеспечивает возможность проектирования на антисимметричное поляризационное состояние (2.175).
Из выражений (2.177), (2.178), (2.182) и (2.183) следует, что в
базисе состояний |
|
±kλ |
|
унитарная матрица |
ˆ |
|
|||||||
|
|
|
|||||||||||
|
|
D , описывающая |
|||||||||||
воздействие светоделителя на поле, имеет вид |
|
|
|||||||||||
ˆ |
T R |
|
|
1 |
|
1 −i |
1 |
(1 |
−iσ1 ) . |
|
|||
D = |
|
|
= |
2 |
|
−i |
= |
2 |
(2.184) |
||||
|
R T |
|
|
1 |
|
|
|
||||||
Интересно отметить, что изложенное выше описание работы светоделителя аналогично стандартному расчету квантовых эффектов отражения и прохождения частицы через одномерный потенциальный барьер (см. задачу 3 в конце этого раздела ).
Перейдем теперь к вопросу о том, как в результате измерения состояния двух фотонов после воздействия светоделителя получается поляризационное состояние Белла (2.175).
Итак, пусть в два входных канала светоделителя приходят два фотона – один слева, другой справа. Один – с вертикальной поляризацией, другой – с горизонтальной. Поскольку это бозоны, вектор исходного состояния системы
|
in = |
1 |
{ |
kv |
1 |
|
− kh |
2 |
+ |
|
− kh |
1 |
|
kv |
2 |
} |
(2.185) |
|
|
|
|
||||||||||||||
|
2 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
симметричен относительно перестановки частиц (1 |
|
|
2 ). Воздей- |
||||||||||||||
ствие светоделителя задается преобразованиями (2.177) и (2.178) для одночастичных векторов состояний, так что состояние системы на выходе имеет следующий вид:
|
out |
|
= |
1 |
× |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
1 |
2 |
1 |
|
|
|
|
|
|
|
(2.186) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
( |
|
|
−kv 1 ) |
( |
|
|
|
2 )+(1 |
|
|||||||
× |
|
|
|
kv |
1 −i |
|
−kh |
2 −i |
kh |
2) |
. |
|||||||
|
2 |
2 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
150 |
|
|
|
|
|
|
|
