
Кулик Введение в теорию квантовых вычислений Книга 2 2008
.pdfТогда решение в области z < 0
Ψ(z < 0)= eikz + Be−ikz
является суперпозицией падающей ( eikz ) и отраженной ( e−ikz ) волн. В области z > 0 есть только прошедшая волна:
Ψ(z > 0)= Ceikz .
Волновая функция Ψ(z)должна быть непрерывной в точке z = 0 , т.е. Ψ(+ 0)= Ψ(− 0)≡ Ψ(0) и удовлетворять условию на
скачок производной Ψ'(+0)−Ψ'(−0)≡ 2m2α Ψ(0), которое свя-
зано с наличием в точке z = 0 сингулярного δ−функционного потенциала. Из этих двух условий получаем уравнение для коэффициентов B и C:
|
|
|
|
1+ B = C |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
mα . |
|
||||||
|
|
|
|
|
|
|
|
(1+ 2iϑ)C, |
ϑ = |
|
|
||||||||||
|
|
|
|
1− B = |
2 |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C = |
|
|
1 |
, B = − |
iϑ |
. |
|
|
|
|
|
|
||||
|
|
|
|
|
1 |
+iϑ |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
1+iϑ |
|
|
|
|
|
|
||||||||
Эти коэффициенты удовлетворяют условию |
|
B |
|
2 + |
|
C |
|
2 |
=1, которое |
||||||||||||
|
|
|
|
||||||||||||||||||
выражает |
тот |
факт, |
что |
плотность |
|
|
потока |
вероятности |
|||||||||||||
j = |
i |
Ψ |
∂Ψ* |
−к.с. |
не зависит от z. Коэффициент C описывает |
||||||||||||||||
|
∂z |
||||||||||||||||||||
|
2m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
амплитуду прошедшей волны, а B – амплитуду отраженной волны.
161

Если ϑ =1, то
С = |
1 |
e−iπ 4 , |
B = − |
i |
e−iπ 4 . |
|
2 |
2 |
|||||
|
|
|
|
Мы видим, что с точностью до общего фазового множителя e−iπ 4 , амплитуды C и B совпадают, соответственно, с выражениями
4 , амплитуды C и B совпадают, соответственно, с выражениями
(2.182) и (2.183).
11. На светоделитель падают два одинаковых по частоте фотона – один слева, другой справа. Фотоны находятся в симметричном перепутанном по поляризациям состоянии (ЭПР-пара)
Ψ(+) 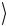 = 12 ( v
= 12 ( v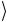 1 h
1 h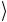 2 + h
2 + h 1 v
1 v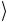 2 ).
2 ).
Где могут быть зарегистрированы фотоны после взаимодействия со светоделителем? По одну или по разные стороны от светоделителя?
Решение
Вектор исходного состояния системы двух фотонов симметричен относительно перестановки частиц (1 2 ) и имеет вид
in = |
1 |
|
|
( |
|
k |
1 |
|
−k |
2 + |
|
|
|
−k 1 |
|
k 2 ) |
|
Ψ(+) = |
|
|||||||
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
= |
1 |
{ |
|
kv |
1 |
|
−kh |
2 + |
|
−kh 1 |
|
kv 2 + (k |
−k)}, |
|||||||||||||
|
|
|
|
|||||||||||||||||||||||
|
||||||||||||||||||||||||||
2 |
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
где ( k −k ) означает, что эти члены получаются изменением знака у волновых векторов.
162

Используя преобразования (2.177) и (2.178), получаем состояние системы на выходе из светоделителя:
|
out |
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
= 1 |
{ ( |
|
kv |
1 −i |
|
−kv 1 )( |
|
−kh |
|
2 −i |
|
kh 2 )+(1 2) +(k |
−k)}= |
|||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||
4 |
|
|
|
|
|
|||||||||||||||||||||||||
i |
{ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
} |
|
|
||
|
|
|
|
|
|
1 |
|
|
|
|
2 |
|
|
|
1 |
|
|
2 |
|
|
|
|
|
|
||||||
= − |
|
|
|
kv |
|
|
kh |
|
|
+ |
|
kh |
|
|
|
|
kv |
|
+(k |
−k) |
= |
|
||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= − |
|
i |
|
( |
|
k |
|
1 |
|
k |
|
2 + |
|
−k 1 |
|
−k |
|
2 ) |
|
Ψ(+) . |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
2 |
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Мы видим, что оба фотона будут иметь одинаковые волновые векторы — либо k, либо –k. Это означает, что после взаимодействия со светоделителем они могут быть зарегистрированы только по одну сторону от светоделителя – либо справа, либо слева. Для выбранного начального условия деструктивная квантовая интерференция обращает в нуль амплитуду вероятности выхода пары фотонов с разными волновыми векторами.
2.5. Двухкубитовые гейты
Произвольное унитарное преобразование в пространстве состояний двухкубитовой системы нельзя сконструировать с помощью только однокубитовых гейтов. Было показано, например, что максимально перепутанные и факторизованные состояния не могут переходить друг в друга под воздействием только однокубитовых операторов. В том, что произвольное двухкубитовое унитарное преобразование не может быть представлено в виде тензорного произведения однокубитовых операторов, можно формально убедиться следующим образом. Любое число унитарных операторов, примененных к одному кубиту, эквивалентно некоторой результи-
рующей унитарной матрице ˆ , которая определяется, как мы зна-
U1
ем, четырьмя действительными параметрами. Поэтому тензорное произведение двух таких произвольных матриц содержит, в общем
163

случае, 4+4–1=7 параметров, поскольку общие фазы суммируются.
Унитарная 4×4 |
ˆ |
двухкубитового преобразования со- |
матрица U2 |
держит 16 комплексных чисел, т.е. 32 действительных параметра,
ˆ + ˆ |
=1 . По- |
на которые накладывается условие унитарности U2 U2 |
скольку 4×4 |
ˆ + ˆ |
2 |
является эрмитовой, то ее диагональ- |
матрица U2 U |
ные элементы действительные, а симметрично расположенные недиагональные элементы комплексно сопряжены по отношению друг к другу. Поэтому из уравнения
|
|
|
a |
b |
b |
b |
|
|
|
|
|
1* |
1 |
2 |
3 |
|
|
ˆ |
+ |
ˆ |
b1 |
a2 |
c1 |
c2 |
|
|
|
= b* |
c* |
a |
d |
=1 |
(2.189) |
||
U2 U2 |
||||||||
|
|
|
2 |
1 |
3 |
1 |
|
|
|
|
|
b* |
c* |
d* |
a |
|
|
|
|
|
3 |
2 |
1 |
4 |
|
|
получаются 4 действительных, |
a1,2,3,4 |
=1, и 6 |
комплексных, |
|||||
b1,2,3 = c1,2 = d1 = 0 , соотношений, т.е. всего 16 действительных условий. Это означает, что для задания произвольной двухкубитовой унитарной матрицы требуется 32–16=16 действительных параметров.
Гейт CNOT
Наиболее важным двухкубитовым гейтом является операция
Controlled NOT (CNOT), т.е. «управляемое НЕ». Как мы увидим,
этот логический элемент играет фундаментальную роль в синтезе любых мультикубитовых гейтов.
Гейт CNOT описывается унитарным оператором
CNOT = |
|
0 0 |
|
I + |
|
1 1 |
|
σ1 , |
(2.190) |
|
|
|
|
который представляет собой сумму двух тензорных произведений. В каждом слагаемом операторы, стоящие слева, действуют на пер-
164
вый кубит, а операторы, стоящие справа – на второй кубит. Первые операторы являются проекторами на базисные состояния 0 и 1
и 1 .
.
На второй кубит действует либо тождественный оператор I, либо σ1 , который описывает однокубитовый элемент NOT (2.56). При
этом воздействие на второй кубит того или иного однокубитового гейта зависит от состояния первого кубита, который, тем самым, управляет преобразованием своего партнера. Первый кубит назы-
вается управляющим, а второй – управляемым.
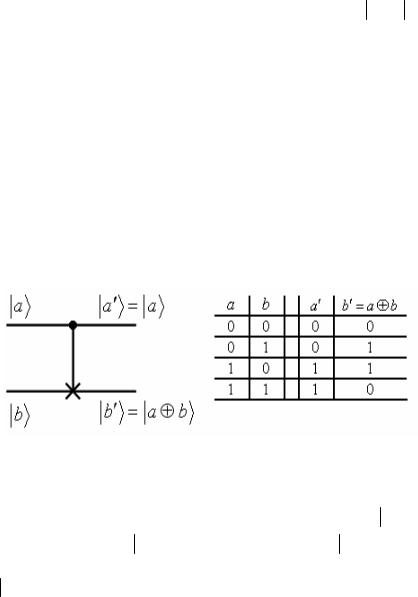
На рис. 2.12 слева изображена квантовая схема операции CNOT. Верхняя линия отвечает управляющему кубиту, а нижняя – управляемому. Темный кружок и крестик, расположенные на этих линиях и соединенные вертикальной прямой, собственно, и представляют операцию CNOT. Темный кружок стоит на линии управляющего кубита, а крестик, изображающий операцию NOT, расположен на линии управляемого кубита.
Рис. 2.12
Из структуры выражения (2.190) видно, что операция CNOT действует следующим образом. Если управляющий кубит a на-
на-
ходится в состоянии 0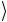 , то с управляемым кубитом b
, то с управляемым кубитом b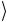 ничего не происходит. Если же управляющий кубит находится в состоянии 1
ничего не происходит. Если же управляющий кубит находится в состоянии 1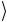 , то управляемый кубит проходит через операцию NOT, т.е. «переворачивается». Обратим внимание еще на одно полезное
, то управляемый кубит проходит через операцию NOT, т.е. «переворачивается». Обратим внимание еще на одно полезное
165

свойство гейта CNOT. Если b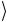 находится сначала в состоянии
находится сначала в состоянии
0 , то после операции CNOT он будет в том же состоянии, что и кубит a
, то после операции CNOT он будет в том же состоянии, что и кубит a , т.е. происходит копирование кубита a
, т.е. происходит копирование кубита a . Для аккурат-
. Для аккурат-
ности заметим, что управляющий кубит свое состояние не меняет. Таблица истинности для начальных (a и b) и конечных ( a′ и b′) значений битов приведена на рис. 2.12 справа.
С точки зрения квантовых вычислений, гейт CNOT осуществляет операцию сложения битов a и b по модулю 2. Эта операция обозначена символом a b , а ее результат записан в выходном со-
стоянии управляемого кубита, b′ = a b
= a b . Тот факт, что в конечном состоянии системы сохраняется состояние управляющего кубита a
. Тот факт, что в конечном состоянии системы сохраняется состояние управляющего кубита a , обеспечивает обратимость данной вычислительной
, обеспечивает обратимость данной вычислительной
операции. Это есть прямое следствие унитарности преобразования
(2.190).
При рассмотрении квантовых схем с участием гейта CNOT оказываются полезными различные представления этой операции.
Подставляя в (2.190) выражение (2.47) и (2.63) для операторов, соответственно, σ1 и I, получаем
CNOT = 0 |
0 ( 0 |
0 + 1 1 ) + |
|
+ 1 1 ( 0 |
1 + 1 |
0 ) = |
(2.191) |
= 00 00 + 01 01 + 10 11 + 11 |
10 . |
||
Это операторное представление показывает, что при унитарном преобразовании CNOT базисные двухкубитовые состояния 00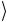 и
и
01 остаются неизменными, а состояния 10
остаются неизменными, а состояния 10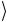 и 11
и 11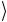 переходят одно в другое. Поэтому повторное применение гейта CNOT возвращает систему к исходному состоянию, т.е. (CNOT )2 =1 , и
переходят одно в другое. Поэтому повторное применение гейта CNOT возвращает систему к исходному состоянию, т.е. (CNOT )2 =1 , и
обратное преобразование (CNOT )−1 совпадает с CNOT.
Из выражения (2.191) так же непосредственно следует вид мат-
166

рицы оператора CNOT в двухкубитовом вычислительном базисе. Действительно, коэффициенты при внешних произведениях базисных кэт-векторов, которые входят в (2.191), суть отличные от нуля матричные элементы оператора CNOT. С методической целью найдем эту матрицу, используя правило (2.138) вычисления кронекерова произведения матриц. Вспоминая матрицы
0 0 |
1 |
0 |
|
, |
|
1 1 |
|
|
0 |
0 |
, |
|||
= |
|
|
|
|
= |
|
|
|
||||||
|
0 |
0 |
|
|
|
|
|
|
|
0 |
1 |
|
|
|
|
1 |
0 |
|
|
σ1 |
0 |
1 |
|
|
|||||
I = |
1 |
, |
|
= |
1 |
0 |
|
|
|
|||||
|
0 |
|
|
|
|
|
|
|
|
|||||
однокубитовых операторов, получаем
|
|
|
1 0 |
|
1 0 0 |
0 |
|
0 |
1 |
= |
|
|
|||||||||||
CNOT = |
0 0 |
|
|
0 1 |
|
+ |
0 |
1 |
|
1 |
|
|
|
||||||||||
|
|
|
|
|
|
|
0 |
|
|
|
|||||||||||||
1 |
0 |
|
0 |
0 |
0 |
0 |
|
0 |
0 |
|
|
1 |
0 |
0 |
0 |
|
. (2.192) |
||||||
|
0 |
1 |
|
0 |
0 |
|
|
0 |
0 |
|
0 |
0 |
|
|
|
0 |
1 |
0 |
0 |
|
|||
= |
|
|
+ |
|
|
= |
|
|
|||||||||||||||
|
0 |
0 |
|
0 |
0 |
|
|
0 |
0 |
|
0 |
1 |
|
|
|
0 |
0 |
0 |
1 |
|
|
||
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
0 |
0 |
|
0 |
0 |
|
0 |
0 |
|
1 |
0 |
|
|
|
0 |
0 |
1 |
0 |
|
|
|||
Пунктирные линии в 4×4 матрицах выполняют роль, как принято говорить, «гида для взгляда», и не более того.
В таблице истинности на рис. 2.12 приведены результаты действия гейта CNOT в тех случаях, когда управляющий кубит a на-
на-
ходится в одном из базисных состояний 0 или 1
или 1 . Представляет интерес рассмотреть такую ситуацию, когда состояние системы на входе имеет вид in
. Представляет интерес рассмотреть такую ситуацию, когда состояние системы на входе имеет вид in = a
= a
 b
b , а управляющий кубит находится в
, а управляющий кубит находится в
произвольном суперпозиционном состоянии a = α 0
= α 0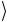 +β 1
+β 1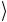 .
.
167

Применение операции CNOT дает
out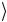 = CNOT in
= CNOT in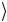 = ( 0
= ( 0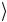
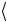 0 I + 1
0 I + 1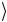
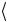 1 NOT ) a
1 NOT ) a
 b
b =
=
= 0 a 0 b + 1 a 1 (NOT b )= |
(2.193) |
= α 0
 b
b +β 1
+β 1
 b
b ,
,
где результат действия операции NOT на управляемый кубит b
обозначен как b . Если b
. Если b = 0
= 0 , то b
, то b = 1
= 1 и
и
|
|
|
|
|
|
b = |
|
|
out |
= α |
|
|
00 +β |
|
11 . |
(2.194) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Аналогично, если |
|
|
1 , то |
|
|
|
= |
|
0 и |
|
|||||||||||||||
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
b |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
out |
= α |
|
01 +β |
|
10 . |
(2.195) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Таким образом, под действием операции CNOT факторизованное |
|||||||||||||||||||||||||
состояние |
|
a |
|
b переходит в |
перепутанное двухкубитовое со- |
||||||||||||||||||||
|
|
||||||||||||||||||||||||
стояние. Наряду с этим, с помощью гейта CNOT можно совершить и обратную операцию, т.е. факторизовать перепутанное состояние, поскольку оператор CNOT совпадает со своим обратным. Именно с этим свойством связана фундаментальная роль логического элемента CNOT при конструировании мультикубитовых гейтов.
Для примера покажем, как с помощью элементарных квантовых гейтов можно создать перепутанное состояние, например, Ψ+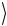 двух кубитов, которые первоначально были в факторизованном базисном состоянии 00
двух кубитов, которые первоначально были в факторизованном базисном состоянии 00 ≡ 0
≡ 0
 0
0 . Протокол такого преобразования изображается схемой, представленной на рис. 2.13.
. Протокол такого преобразования изображается схемой, представленной на рис. 2.13.
168

0 |
H |
0 |
Рис. 2.13
Соответствующая последовательность операций выглядит так:
|
00 → 01 |
→ |
0 |
+ |
1 |
1 |
→ |
|||||||||||
|
NOT2 |
|
|
|
|
|
H1 |
|
|
|
|
CNOT |
||||||
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
, (2.196) |
|
|
|
( |
|
|
|
|
)≡ |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
CNOT |
|
|
|
|
|
|
+ |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|||||||||
→ |
|
|
|
01 |
+ |
10 |
Ψ |
|
|
|
|
|||||||
|
2 |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
т.е. сначала совершаются операция NOT (σ1 ) над вторым кубитом и преобразование Адамара (H) над первым кубитом, а заключительный гейт CNOT переводит систему в состояние Белла Ψ+ .
.
Применяя далее к этому состоянию однокубитовые гейты σi ,
можно получить, как следует из соотношений типа (2.169) – (2.170), остальные состояния Белла.
Иногда бывает удобно модифицировать гейт CNOT к виду
CNOT = |
|
0 0 |
|
σ1 + |
|
1 1 |
|
I . |
(2.197) |
|
|
|
|
В этом случае состояния 0 и 1
и 1 управляющего кубита поменя-
управляющего кубита поменя-
лись ролями. Теперь управляемый кубит подвергается операции NOT в том случае, когда управляющий кубит находится в состоя-
нии 0 .
.
169
Матрица преобразования (2.197) выглядит так:
0 |
1 |
0 |
0 |
|
|
|
|
1 |
0 |
0 |
0 |
|
|
CNOT = |
. |
(2.198) |
||||
|
0 |
0 |
1 |
0 |
|
|
|
|
|
||||
|
0 |
0 |
0 |
1 |
|
|
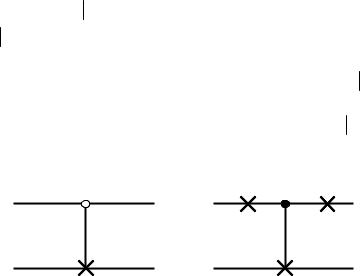
На рис. 2.14 слева изображена квантовая схема операции CNOT . На линии управляющего кубита теперь нарисован светлый кружок. Справа показана эквивалентная схема, которая отличается от гейта CNOT двумя дополнительными однокубитовыми операциями NOT на линии управляющего кубита. Роль этих однокубитовых гейтов сводится к тому, что исходное состояние управляющего кубита сначала подвергается операции NOT, а после обычного гейта CNOT возвращается назад. Легко убедиться в эквивалентности квантовых схем. Пусть, например, сначала управляющий кубит
был в состоянии 0 . После операции NOT он переходит в состоя-
. После операции NOT он переходит в состоя-
ние 1 . Затем следует обычная операция CNOT, которая изменяет состояние управляемого кубита. Наконец, последняя операция NOT возвращает управляющий кубит в исходное состояние 0
. Затем следует обычная операция CNOT, которая изменяет состояние управляемого кубита. Наконец, последняя операция NOT возвращает управляющий кубит в исходное состояние 0 . В результате получилось, что операция NOT применяется ко второму кубиту, если управляющий кубит находится в состоянии 0
. В результате получилось, что операция NOT применяется ко второму кубиту, если управляющий кубит находится в состоянии 0 . Это
. Это
соответствует гейту CNOT .
=
Рис. 2.14
170
