Кулик Введение в теорию квантовых вычислений Книга 2 2008

Точно так же проверяется, что преобразование остальных базисных состояний

ˆ	= w 00 + z 10 ,
10 → (U 1 ) 0

01 → 01,

11→ 11

эквивалентно действию матрицы (2.218) на соответствующие век- тор-столбцы.

Так как операция «управляемое U» выражается, как было показано ранее, через однокубитовые преобразования и гейты CNOT, то это утверждение справедливо и для квантовой схемы, которая представлена на рис. 2.18 и отвечает матрице (2.218). Аналогичным образом строятся еще две квантовые схемы, которые отвечают

матрицам, перемешивающим состояния 00 и 01 , а также 01

и 11 . Они предлагаются в качестве задачи в конце данного разде-

ла. Еще раз подчеркнем, что все эти схемы относятся к преобразованиям, которые перемешивают пару базисных состояний, отличающихся значением одного бита, с помощью однокубитовой под-

матрицы ˆ . Поэтому рецепт построения таких схем очевиден:

U

кубит с совпадающим для двух перемешиваемых состояний значением бита надо взять в качестве управляющего и совершить над другим кубитом преобразование типа «управляемое U».

Рассмотрим теперь двухуровневую матрицу

	1		0	0	0
		0	u	w	0
							.	(2.219)
		0	v	z	0
		0	0	0	1

Она перемешивает два базисных состояния 01 и 10 , которые отличаются значениями двух битов. Чтобы использовать подмат-

181

ˆ	u w		как однокубитовое преобразование, надо поме-
рицу U =
	v	z

нять местами состояния 01 и 00 , не затрагивая другие базисные векторы. Такая перестановка осуществляется с помощью операции CNOT . После этого состояния 00 и 10 отличаются зна-

чением только одного бита, и можно применить операцию «управляемое U», в которой управляющее воздействие осуществляется

вторым кубитом в состоянии 0 . На последнем шаге надо с по-

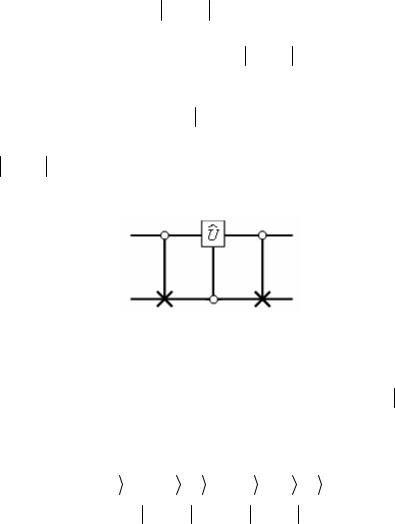
мощью гейта CNOT совершить обратную перестановку состояний 00 и 01 . Описанная квантовая схема показана на рис. 2.19.

Рис. 2.19

Рассмотрим для примера действие этой схемы на состояние 10 .

Поскольку в этом случае первая операция CNOT не работает, то цепочка преобразований входного состояния выглядит так:

	ˆ		1 )		0	= (w		0 + z		1 )		0 =
	10 → (U
												(2.220)

= w 00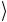+ z 10 → w 01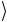+ z 10.

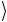Это, конечно, совпадает с результатом действия матрицы (2.219) на соответствующий вектор-столбец. Аналогичным образом строится квантовая схема для матрицы, перемешивающей базисные состоя-

182

ния 00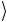 и 11 . Заметим, что процедура построения этих схем

отличается от предыдущего рецепта дополнительным преобразованием, которое выравнивает значения одного из битов, делая тем

самым возможным применение однокубитовой операции ˆ .

U

Можно показать (см. задачу 4 в конце этого раздела), что любая унитарная матрица записывается в виде конечного произведения унитарных двухуровневых матриц. С учетом этого свойства утверждение о том, что однокубитовые преобразования и операция CNOT составляют универсальный набор гейтов, является доказанным. Ради аккуратности заметим, что пока мы ограничились двухкубитовыми операциями. Представляется, однако, вполне очевидным, что рецепты построения квантовых схем могут быть обобщены на случай любых мультикубитовых гейтов. Мы вернемся к этому вопросу в разделе 2.6.

Неклонируемость квантовых состояний

Классическую информацию можно неограниченно копировать с помощью процессов, которые не зависят от сути копируемой информации и никак не влияют на нее. Это делает и компьютер, и светокопировальное устройство, да и самая обычная пишущая машинка.

Иначе обстоит дело с квантовой информацией, носителем которой являются кубиты. Свойства квантового копирования являются еще одним примером разительного различия квантовой и классической информации.

Уточним постановку задачи. Пусть имеются две одинаковые по своим физическим свойствам квантовые системы. Одна из них находится в некотором чистом квантовом состоянии, кэт-вектор

которого Ψ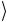 произволен и, в общем случае, нам не известен. Вторая система находится в каком-то известном начальном состоянии 0 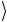. Вопрос в том, существует ли для этих квантовых систем ка- кой-нибудь универсальный процесс, который, не меняя состояние первой системы, переводит вторую в состояние Ψ 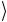, т.е. создает копию произвольного квантового состояния. Такой процесс можно

183

назвать квантовым клонированием. Отрицательный ответ на поставленный вопрос дает теорема о неклонируемости квантовых состояний, которая была сформулирована в 1982 г. Вуттерсом и Зуреком, а также Диксом.

Суть теоремы достаточно проста, и ее можно доказать, исходя из свойств унитарных преобразований двухкубитовой системы. Пусть эта система находится в факторизованном начальном со-

стоянии

Ψ

0 , где кэт-вектор

Ψ первого кубита подлежит кло-

нированию с помощью

некоторого унитарного

двухкубитового

ˆ

преобразования C , т.е.

ˆ

Ψ

0

=

Ψ

Ψ .

(2.221)

C

Если вспомнить, например, операцию CNOT (2.190), то она производит копирование базисных состояний первого кубита:

CNOT 0 0 = 0 0,

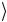
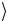
CNOT 1 0 = 11.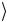

Если же первый кубит находится в произвольном суперпозиционном состоянии Ψ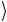 = α 0+β 1 , то состояние системы на выходе имеет вид (2.194):

CNOT Ψ 0 = α 00+β 11 ≠ Ψ Ψ ,

т.е. оно является перепутанным состоянием двух кубитов, а не факторизованным. Приведенный пример показывает, что копирование

с помощью гейта CNOT двух ортогональных состояний 0 и 1

возможно, но при этом неортогональное им состояние Ψ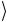 клонировать нельзя.

Рассмотрим теперь произвольный оператор клонирования ˆ .

C

Поскольку он должен копировать любые исходные состояния пер-

184

вого кубита, то для двух таких состояний Ψ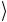 и Φ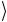 имеем:

ˆ

Ψ

0

=

Ψ

Ψ ,

C

ˆ

(2.222)

Φ

0

=

Φ

Φ .

C

Из условия сохранения скалярного произведения при унитарном преобразовании получаем:

Φ

Ψ = ( Φ

Ψ )2 .

(2.223)

Поэтому либо

Φ

Ψ = 0 ,

(2.224)

т.е. состояния

Ψ и

Φ ортогональны, либо

Φ

Ψ =1 , что с

учетом нормировки дает совершенно неинтересное соотношение

Ψ = Φ .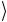

Таким образом, доказано, что не существует унитарного оператора, который может клонировать два различных неортогональных состояния. Основное содержание утверждения может быть распространено на более общие постановки задачи.

Невозможность клонирования неортогональных квантовых состояний играет ключевую роль в квантовой криптографии. Тот факт, что нельзя получить копию некоторого неизвестного нам произвольного квантового состояния, означает также, что, не разрушив состояние системы, невозможно получить информацию об этом состоянии. Этот аспект теоремы неклонируемости оказывается очень важным для правильной интерпретации результатов измерений перепутанных состояний, которые проводятся разными участниками квантовой коммуникационной схемы.

185

Задачи

1. Для системы двух кубитов построить квантовые схемы, отвечающие унитарным двухуровневым матрицам, которые перемешивают базисные состояния:

(а)

00 и

10 ,

(б)

01 и

11 .

2. Проверить, что квантовая схема

U

отвечает двухуровневой матрице, которая перемешивает базисные

состояния		00 и		11 спомощью унитарной 2×2	ˆ
					подматрицы U .
3. Показать, что квантовая схема

описывает операцию перестановки кубитов. Сравнить со схемой,

ˆ	=σ1 .
показанной на рис. 2.19, если в той положить U

4. Показать, что унитарную матрицу можно представить в виде конечного произведения унитарных двухуровневых матриц.

186

Решение

Сначала рассмотрим для примера унитарную матрицу 3×3

	a	.	.
ˆ		.
U = b			. .
		.
	c		.

В ней вписаны в явном виде только те элементы, за которыми мы будем следить в процессе дальнейших вычислений. Напомним, что

условие унитарности ˆ + ˆ = приводит к равенству

U U 1

a 2 + b 2 + c 2 =1. Аналогичные равенства имеют место для элементов каждой строки и каждого столбца. Найдем такую унитар-

ˆ , которая удовлетворяет соотношению ную матрицу U1

a′

ˆ ˆ =

U1U 0

c′

.	.
.
	. .
.
	.

Решив несложную систему двух линейных алгебраических уравнений, получаем

			*			*
ˆ	a			d	b		d	0		,
U1	=	−b d a d 0
			0			0		1

где d =

a

2

+

b

2

. Матрица

ˆ

очевидно, унитарной и

U1 является,

ˆ

ˆ

a′ = d

двухуровневой. Вычислив произведение U1U , находим, что

и c′ = c , т.е.

d .

.

ˆ ˆ

U1U

= 0 .

. .

c .

.

187

Теперь ищем матрицу ˆ , которая удовлетворяет соотношению

U2

	1 0		0
ˆ ˆ ˆ		0 .	.
U2U1U	=			.
		0 .	.

Простые алгебраические вычисления дают следующее выражение

для унитарной двухуровневой матрицы ˆ

U2 :

		d	0	c	*
ˆ
U2	=	0	0	0		.
		−c	0	d

ˆ	ˆ	ˆ	– унитарные матрицы, то их произведение
Так как U , U1		и U2
						1	0	0
			ˆ ˆ ˆ	ˆ		0
		U2U1U		=U3	=		u w
						0	v
								z

представляет собой двухуровневую унитарную матрицу ˆ

U3 , в ко-

торой выделилась унитарная подматрица	u	w	. После этого
	v	z

исходная матрица ˆ окончательно записывается в виде

U

ˆ = ˆ + ˆ + ˆ

U U1 U2 U3

произведения трех унитарных двухуровневых матриц, что и требовалось доказать.

Применительно к общему случаю унитарной матрицы r ×r изложенная схема вычислений работает следующим образом.

188

Сначала умножаем исходную матрицу ˆ на − подходя-

U (r 1)

щую двухуровневую матрицу. Элементы каждой матрицы этой последовательности находятся из линейных алгебраических уравнений, которые задаются условием обращения в нуль очередного элемента первого столбца получившегося произведения матриц. В результате получается матрица вида

1		0	0
	0	. . .
		. . .		.
	0
		. . .	r−1	r

Здесь индексы r и r −1 указывают размерности соответствующих матриц. Затем умножаем на такие (r −2) двухуровневые матрицы, чтобы уже в выделенной подматрице с размерностью (r −1)×(r −1) обратить в нуль все элементы первого столбца,

кроме диагонального. Из-за условия унитарности будут равны нулю и соответствующие элементы первой строки. Продолжаем эту процедуру до тех пор, пока все произведение не превратится в двухуровневую матрицу, которая в правом нижнем углу содержит унитарную 2×2 подматрицу, а из остальных элементов отличны от нуля и равны единице только диагональные. Умножая на обратные матрицы, приходим к окончательному выражению для исход-

ной матрицы ˆ

U

ˆ ˆ ˆ	ˆ
U =V1V2	Vk

в виде произведения k штук унитарных двухуровневых матриц. Среди этих матриц могут быть единичные, так что k ≤ r ( r −1)/2. Унитарные преобразования n-кубитового регистра описываются матрицами 2n ×2n . Поэтому d = 2n и k ≤ 2n−1 (2n −1).

189

5. Доказать эквивалентность квантовых схем:

а)

б)

в)

Указание

Случай в) рассмотреть с помощью базисов {|0 , |1 } и { 12 ( 0± 1) }.

190