
Кулик Введение в теорию квантовых вычислений Книга 2 2008
.pdf
Задачи
1.С помощью формулы (2.132) вычислить тензорные произведения вектор-столбцов, соответствующих базисным состояниям кубита, и получить вектор-столбцы, которые описывают базисные состояния двухкубитовой системы.
2.Для системы трех кубитов
(а) Написать кэт-векторы базисных состояний, используя однокубитовые состояния 0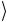 и 1
и 1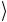 .
.
(б) Написать спинорное представление этих векторов.
(в) Получить их как тензорное произведение базисных вектор-столбцов трех кубитов.
3.Рассмотреть две эквивалентные квантовые схемы c1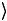
 I
I
≡U = I U
c0 
 U
U 
Написать матрицу двухкубитового гейта I U , который является тензорным произведением однокубитовых гейтов I и U .
4. Рассмотреть две эквивалентные квантовые схемы и найти мат-
рицу двухкубитового гейта σ1 2 ≡ σ1 σ1 . Как он действует на двухкубитовый базис?
|
c1 |
|
|
|
|
|
|
|
|
|
|
≡ |
|
|
σ1 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
c0 |
|
|
|
|
|
|
|
|
H n |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
5. Доказать, что оператор |
|
|
|
|
|
|
|||||||||||
|
можно представить в виде |
||||||||||||||||
H n = 2−n 2 |
∑( |
−1 s t |
|
s t |
|
, |
где |
|
s |
обозначает базисные векторы |
|||||||
|
|
|
|||||||||||||||
|
|
|
|||||||||||||||
|
|
|
) |
|
|
|
|
||||||||||
|
|
|
s,t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2.110) n-кубитового регистра. |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
131 |
|
|
|
|
|
|||
2.4. Перепутанные состояния
Применение принципа суперпозиции к составной квантовой системе с неизбежностью приводит к появлению перепутанных квантовых состояний подсистем. Поэтому, с точки зрения законов квантовой механики, перепутанные состояния являются вполне рутинным свойством составных систем. Такие системы являются, очевидно, стандартным объектом квантово-механических расчетов. При этом перепутывание состояний подсистем учитывается автоматически и не требует никакого специального внимания.
Интрига заключена в той роли, которую играют перепутанные состояния в квантовой информации. Первый намек на существование специфической связи между теорией информации и квантовой физикой восходит к 1935 г., когда Альберт Эйнштейн, Борис Подольский и Натан Розен в статье под заголовком «Можно ли считать квантово-механическое описание физической реальности полным?» (Phys. Rev., 1935, V.47, P.777–780) сформулировали свой знаменитый парадокс, отражающий одну из принципиальных особенностей квантового мира, о которой теперь принято говорить как об отсутствии локального реализма. Суть в том, что перепутывание квантовых состояний может выражаться в столь высокой степени корреляции между подсистемами, которую невозможно описать в терминах только локальных характеристик этих подсистем. Такие корреляции существенным образом влияют на процессы манипулирования квантовой информацией. Важность явления перепутывания была понята Эрвином Шрёдингером, который в том же 1935 г. опубликовал серию статей под общим заголовком «Современная ситуация в квантовой механике» (Die Naturwissenschaften, 1935, V. 23, P. 807-812, 823-828, 844-849). В
этой работе, одним из побудительных мотивов которой явилось обсуждение вопросов, поставленных в статье тремя авторами, были проанализированы основы квантово-механического описания состояний физических систем и процессов измерения. В том числе было введено само понятие перепутывания двух квантовых систем
(от немецкого Verchraenktheit zweier Quantesysteme). Две кванто-
вые системы, находящиеся в перепутанном состоянии, называют ЭПР-парой. С количественным описанием степени корреляции
132
перепутанных состояний связаны так называемые неравенства Белла, сформулированные в 1964 г. (Bell J.S. On the Einstein- Podolsky-Rosen paradox //Physics, 1964, V.1, P.195). Квантовая ин-
формация придала этим проблемам, лежащим в основаниях квантовой механики, современное звучание.
Cложение двух спинов
Рассмотрим спиновые состояния системы, состоящей из двух
частиц со спинами s1 = s2 |
=1 2 . Операторы спинов этих подсис- |
|
ˆ |
ˆ |
|
тем обозначаются как s1 и |
s2 . Для квадратов этих операторов вы- |
|
ˆ2 |
ˆ2 |
= s1 (s1 +1) = 3 4 . В качестве одно- |
полняется соотношение s1 |
= s2 |
|
частичных базисных векторов |
выберем, как обычно, состояния |
|
σ (1),(2) с определенными значениями σ(1),(2) = ± 1 |
2 |
проекций |
|
|
спинов каждой из подсистем 1 и 2 на некоторую ось квантования z. Тогда четыре кет-вектора
σ (1) |
σ (2) ≡ |
|
±1 2 |
1 |
|
±1 2 |
2 |
(2.148) |
|
|
|||||||
|
|
|
|
|
|
|
образуют полный набор двухчастичных спиновых состояний. Именно такие состояния мы использовали в предыдущем разделе в качестве базиса двухкубитового регистра. Подчеркнем, что в этих состояниях проекция спина каждой частицы на ось z имеет определенное значение. При поворотах системы координат происходит изменение каждой из этих проекций, и все базисные состояния (2.148) перемешиваются друг с другом.
Представляет интерес другой базис, в котором спиновые состояния классифицируются по величине суммарного спина системы. Сейчас мы покажем, что суммарный спин принимает два значения, 1 и 0, а пространство спиновых состояний разбивается на два инвариантных подпространства, отвечающих этим значениям полного спина.
При повороте системы координат спиновые состояния Ψ(1) и
и
Ψ(2) подсистем преобразуются по закону (2.26) с генераторами,
подсистем преобразуются по закону (2.26) с генераторами,
133

ˆ |
и |
ˆ |
. Спиновое состояние |
|
Ψ(1,2) всей систе- |
|
|||||
соответственно, s1 |
s2 |
|
|||
мы преобразуется |
так же, как тензорное произведение |
||||
Ψ(1) Ψ(2)
Ψ(2) , т.е. закон преобразования определяется тензор-
, т.е. закон преобразования определяется тензор-
ным произведением операторов поворота для каждой из подсистем:
ˆ |
ˆ |
||
Ψ′(1,2) = eiΦns1 |
eiΦns2 |
|
Ψ(1,2) = |
|
|||
(2.149)
Φˆ
=ei nS Ψ(1,2) .
Здесь
ˆ |
ˆ |
ˆ |
(2.150) |
S |
= s1 |
+ s2 |
есть векторный оператор суммарного спина, компоненты которого
ˆ ( ) подчиняются коммутационным соотношениям (2.28).
Si i=x ,y ,z
Из этих соотношений следует, как уже говорилось в разделе 2.2,
ˆ2 |
ˆ |
могут быть диагонализованы одновре- |
что: (1) операторы S |
и Sz |
ˆ2 |
равны S(S +1) , где S ≥ 0 ; |
менно; (2) собственные значения S |
(3) собственные значения μ оператора ˆ есть действительные
Sz
числа, лежащие в пределах от –S до S через единицу. Поэтому вопрос сводится к определению возможных значений величины сум-
марного спина S при заданных значениях s1 и s2 спинов подсис-
тем. Это есть теорема о сложении моментов. Хотя общий случай не представляет никаких затруднений, ограничимся, для простоты,
только интересующей нас ситуацией, когда s1 = s2 =1 2 .
2 .
Собственные векторы операторов |
ˆ |
2 |
ˆ |
обозначим как |
|
S |
|
и Sz |
|||
S, μ |
ˆ |
+ sˆ2z |
. Поэтому собственные |
||
. Из (2.150) следует, что Sz = sˆ1z |
|||||
|
134 |
|
|
|
|

значения этих операторов удовлетворяют соотношению
μ =σ(1) +σ(2) . |
(2.151) |
Каждое из состояний S, μ можно разложить по полному базису (2.148):
можно разложить по полному базису (2.148):
∑ CSμ (1) (2)
σ(1)σ ( 2 )
σ(1) +σ ( 2) =μ
Вэтой формуле суммирование по σ (1) и σ (2) ограничено условием.S, =μ σσ (2.152)
(2.151), а CσS(1)μ σ( 2) называются коэффициентами Клебша-Гордана.
Легко видеть, что есть единственное состояние с максимальными проекциями σ(1) =σ(2) =1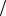 2 . В этом случае μ =1 . Так как это максимальное возможное значение проекции суммарного спина на ось z, то ему отвечает значение квантового числа S = max μ =1. Далее, есть два состояния с противоположными значениями проекций спинов, σ(1) = −σ(2) =1
2 . В этом случае μ =1 . Так как это максимальное возможное значение проекции суммарного спина на ось z, то ему отвечает значение квантового числа S = max μ =1. Далее, есть два состояния с противоположными значениями проекций спинов, σ(1) = −σ(2) =1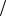 2 и σ(1) = −σ(2) = −1
2 и σ(1) = −σ(2) = −1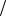 2 , которые дают μ = 0 . Из этих двух линейно независимых состояний можно
2 , которые дают μ = 0 . Из этих двух линейно независимых состояний можно
образовать две линейно независимые суперпозиции вида (2.152). Одна из них будет представлять состояние с уже известным значением S =1 полного спина, но с проекцией μ = S −1 = 0 , которая
на единицу меньше максимальной. Тогда вторая линейно независимая суперпозиция должна относиться к состоянию с другим значением квантового числа S, а именно, к S = 0, для которого μ = 0
является максимально возможным значением проекции. Наконец, последнее оставшееся состояние, для которого σ(1) =σ(2) = −1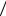 2 и μ = −1 отвечает суммарному спину S =1 и минимально возможному значению проекции,
2 и μ = −1 отвечает суммарному спину S =1 и минимально возможному значению проекции,
min μ = − S = –1.
135
Таким образом, два спина 1/2 могут сложиться в суммарный спин1 S = 1,0. При S =1 есть три состояния с проекциями μ =0, ±1.
Их называют триплетом. При S = 0 есть одно состояние с проекцией μ =0. Это синглет.
При преобразовании поворота (2.149) величина S не меняется,
ˆ2 |
ˆ |
, и, |
так как оператор S |
коммутирует со всеми генераторами Si |
следовательно, с полным оператором вращений. Это означает, что состояния с S = 1 и с S = 0 при вращениях преобразуются сами через себя, образуя инвариантные подпространства.
Кэт-векторы S, μ являются собственными состояниями пол-
являются собственными состояниями пол-
ˆ2 |
ˆ |
. Поэтому они образуют полный |
ного набора операторов S |
и Sz |
ортонормированный базис. С прежним базисом (2.148) он связан соотношением (2.152), которое представляет собой унитарное преобразование, заданное матрицей коэффициентов Клебша-Гордана.
Найдем явный вид спиновых состояний S, μ системы с определенными значениями суммарного спина S и его проекции μ на
системы с определенными значениями суммарного спина S и его проекции μ на
ось z. Это эквивалентно нахождению коэффициентов КлебшаГордана.
Поскольку максимальная проекция μ =1, отвечающая спину
S=1, может быть получена, как говорилось выше, единственным образом, то в разложении (2.152) присутствует только одно слагаемое, т.е.
|
1,1 = |
|
1 2 1 |
|
1 2 2 . |
(2.153) |
|
|
|
||||
|
|
|
|
Аналогично, для минимальной проекции μ = −1 имеем
|
1, −1 = |
|
−1 2 1 |
|
−1 2 2 . |
(2.154) |
|
|
|
||||
|
|
|
|
1 В общем случае при сложении двух спинов s1 и s2 суммарный спин S
может принимать значения от s1 + s2 до s1 − s2 через единицу.
136

В состояние с S = 1 и μ = 0 дают вклад два слагаемых
|
1,0 = a |
|
1 2 1 |
|
−1 2 2 +b |
|
−1 2 1 |
|
1 2 2 . |
(2.155) |
|
|
|
|
|
||||||
|
|
|
|
|
|
Для нахождения коэффициентов Клебша-Гордана, которые здесь для краткости обозначены как a и b, поступим следующим образом. Рассмотрим оператор
|
|
|
ˆ |
ˆ |
ˆ |
|
ˆ |
ˆ |
− , |
(2.156) |
|
|
|
S− = Sx |
−iSy |
= S1− + S2 |
|||||
ˆ |
ˆ |
ˆ |
ˆ |
ˆ |
ˆ |
|
являются операторами, кото- |
|||
где S1− = S1x −iS1y |
и S2− = S2x −iS2 y |
|||||||||
рые понижают на единицу проекцию спина первой и второй части-
|
|
|
|
|
ˆ |
пони- |
цы (см. задачу 1 в конце раздела 2.2). Поэтому оператор S− |
||||||
жает на единицу проекцию полного спина, т.е. |
|
|
||||
ˆ |
|
1,1 = const |
|
1,0 . |
(2.157) |
|
|
|
|||||
S− |
|
|
||||
Выражение, стоящее в левой части этого соотношения, симметрично относительно перестановки индексов 1 и 2, обозначающих
подсистемы. Действительно, состояние 1,1 описывается выражением (2.153), которое не меняется при замене 1 2 . Оператор
описывается выражением (2.153), которое не меняется при замене 1 2 . Оператор
ˆ− (2.156) тоже не меняется при такой замене. Следовательно, век-
S
тор состояния 1,0 , который имеет вид (2.155), должен быть симметричным относительно перестановки частиц. Это означает, что a = b . С учетом условия нормировки
, который имеет вид (2.155), должен быть симметричным относительно перестановки частиц. Это означает, что a = b . С учетом условия нормировки  1,0 1,0
1,0 1,0 =1 получаем, что состояние (2.155) имеет следующий вид:
=1 получаем, что состояние (2.155) имеет следующий вид:
|
1,0 = |
1 |
{ |
|
1 2 1 |
|
−1 2 2 + |
|
−1 2 1 |
|
1 2 2}. |
(2.158) |
|
|
|
|
|
||||||||
|
2 |
|||||||||||
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
137
Таким образом, триплет состояний с S =1 описывается формулами (2.153), (2.154) и (2.158). Все эти состояния симметричны относительно операции перестановки частиц.
В синглетное состояние с |
S = 0 и μ = 0 тоже дают вклад два |
|||||||||||||||||||||||||||||
слагаемых |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
0,0 |
= a |
|
1 2 1 |
|
|
−1 2 2 +b |
|
−1 2 1 |
|
1 2 2 . |
(2.159) |
||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Поскольку |
это |
состояние |
|
|
отвечает |
|
|
|
|
собственному |
значению |
|||||||||||||||||||
Sˆ 2 = S(S +1) = 0 , то оно должно быть ортогонально состоянию |
||||||||||||||||||||||||||||||
(2.158), |
для |
|
которого |
ˆ |
2 |
= S(S +1) = 2 . |
Тогда |
|||||||||||||||||||||||
|
S |
|
||||||||||||||||||||||||||||
1,0 |
|
0,0 = 0 = (a +b) |
|
|
2 , т.е. |
b = −a . С учетом условия норми- |
||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||
ровки имеем окончательно следующее выражение: |
|
|||||||||||||||||||||||||||||
|
|
|
|
|
0,0 |
= |
1 |
{ |
|
1 2 |
1 |
|
|
−1 2 2 − |
|
−1 2 1 |
|
1 2 2}. |
(2.160) |
|||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
2 |
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Мы видим, что синглетное состояние антисимметрично относительно перестановки частиц.
Перепутанные спиновые состояния. Состояния Белла
Векторы состояний (2.153) и (2.154) имеют факторизованный вид, и каждая из частиц находится в чистом спиновом состоянии с определенной проекцией спина на ось z. Это означает, что измерение проекции спина одной из подсистем даст с достоверностью определенный результат.
Иная ситуация с векторами состояний (2.158) и (2.160). Эти состояния не имеют факторизованного вида. Проекция спина ни той, ни другой подсистем не имеет определенного значения, а с равны-
ми вероятностями может быть равной и 1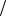 2 , и −1
2 , и −1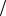 2 . При этом
2 . При этом
спиновые состояния подсистем жестко (на все 100 %) скоррелированны друг с другом. Имеется в виду, что результат совместного
138
измерения спинов подсистем проявляет максимальную степень корреляции. Действительно, произведем измерение проекции спина, например, первой частицы и получим тот или иной результат:
либо 1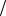 2 , либо −1
2 , либо −1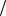 2 . Любой из этих результатов является случай-
2 . Любой из этих результатов является случай-
ным. Тогда вторая частица, которая не имела определенной проекции спина, после измерения, произведенного не над ней, а над другой частицей, будет с достоверностью находиться в состоянии с определенной, а именно, с противоположной проекцией спина. Например, если измерение проекции спина первой частицы дало
результат +1 2 , то последующее измерение проекции спина второй частицы даст с достоверностью значение −1
2 , то последующее измерение проекции спина второй частицы даст с достоверностью значение −1 2 . Тем самым
2 . Тем самым
значение указанной проекции оказывается однозначно скоррелированным со случайным результатом измерения, произведенного над первой частицей.
Подчеркнем, что между частицами нет никакого взаимодействия. Они могут, например, находиться сколь угодно далеко друг от друга. Тогда кажущуюся парадоксальность ситуации можно выразить в виде следующего рассуждения по поводу спинового состояния одной из частиц, например второй. Сначала ее спиновое состояние было полностью неопределенным, так как в состоянии (2.158) или (2.160) обе возможные проекции спина этой частицы являются равноправными. Но как только измерена проекция спина первой частицы, с которой наша частица никак не взаимодействует, ее спиновое состояние становится совершенно определенным. Такая корреляция означает наличие у квантовых объектов качеств, которые нельзя описать в терминах только локальных характеристик этих объектов. Подобные корреляции не имеют аналога в классическом мире.
Состояния (2.158) и (2.160) являются перепутанными спиновыми состояниями. Поскольку проекция спина каждой из подсистем принимает с равными вероятностями любое из своих возможных значений, то такие состояния называются максимально перепутанными.
Заметим, что из факторизованных векторов состояний (2.153) и (2.154) можно построить еще два линейно независимых максимально перепутанных состояния.
139
Взяв симметричную и антисимметричную комбинации выраже-
ний (2.153) и (2.154), получаем:
1 |
{ |
|
1,1 ± |
|
1, −1 }= |
1 |
{ |
|
1 2 1 |
|
1 2 2 ± |
|
−1 2 1 |
|
−1 2 2}. (2.161) |
|
|
|
|
|
|
|
|||||||||||
2 |
2 |
|||||||||||||||
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Совокупность четырех состояний (2.158), (2.160) и (2.161) образует полный ортонормированный базис, состоящий из максимально перепутанных спиновых состояний. Их называют состояниями Белла.
Отождествляя, как обычно, два спиновых состояния с кубитом, т.е. 1 2
2 ≡ 0
≡ 0 и −1
и −1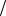 2
2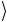 ≡ 1
≡ 1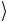 , запишем четыре состояния Белла в следующем виде:
, запишем четыре состояния Белла в следующем виде:
Φ(±) |
= |
|
1 |
|
{ |
|
|
00 |
± |
|
|
|
11 |
}, |
(2.162) |
||
|
|
|
|||||||||||||||
2 |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
Ψ(±) |
= |
|
1 |
{ |
|
01 |
± |
|
10 |
}. |
(2.163) |
||||||
|
|
|
|||||||||||||||
|
2 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||
Во избежание недоразумений заметим, что в этих последних выражениях символы 0 и 1, написанные внутри кэт-векторов, не следует путать с обозначениями величины спина и его проекции, как это было в предыдущих формулах.
Рассмотрим теперь некоторые свойства максимально перепутанных состояний на примере синглетного состояния (2.160) с нулевым суммарным спином. В соответствии с обозначениями
(2.163) это есть двухкубитовое состояние Белла Ψ(−)  , т.е.
, т.е.
Ψ(−) = |
1 |
{ |
|
1 2 1 |
|
−1 2 |
2 − |
|
−1 2 1 |
|
1 2 2}= |
|
||||||||||
|
|
|
|
|
||||||||||||||||||
2 |
(2.164) |
|||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
= |
1 |
1 |
0 − |
0 |
1 |
|
. |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
2 |
|
|
0 |
|
|
|
|
|||||||||||||
|
|
|
|
1 |
2 |
|
1 |
0 |
2 |
|
||||||||||||
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
140 |
|
|
|
|
|
|
|
|
|
|
||
