Электростатика. 16.7

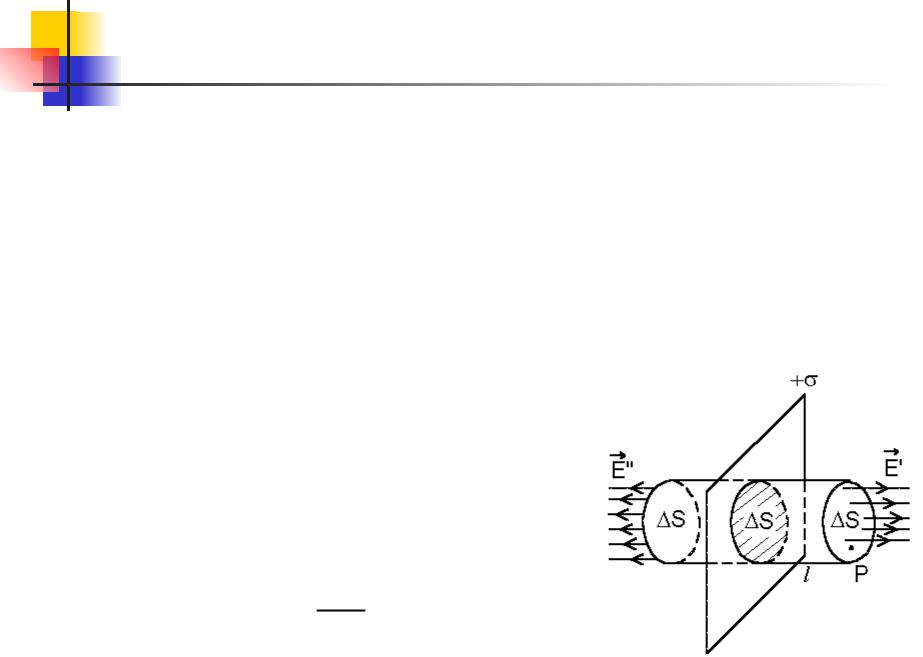
Поле равномерно заряженной плоскости.

Пусть поверхностная плотность заряда равна σ. Из симметрии задачи, очевидно, что вектор Е может быть только перпендикулярным заряженной плоскости. Кроме того, ясно, что в симметричных относительно этой плоскости точках вектор Е одинаков по модулю и противоположен по направлению. Такая конфигурация поля подсказывает, что в

качестве замкнутой поверхности следует выбрать прямой

цилиндрсквозьоснованиями параллелстьными Поток боковую поверхно этого

цилиндра равен нулю, и поэтому полный поток через всю поверхность цилиндра будет 2EΔS, где ΔS – площадь каждого торца цилиндра. Внутри цилиндра заключен заряд σΔS. Согласно теореме

Гаусса 2EΔS= σΔS откуда получаем:

E 2 0

Электростатика. 16.8

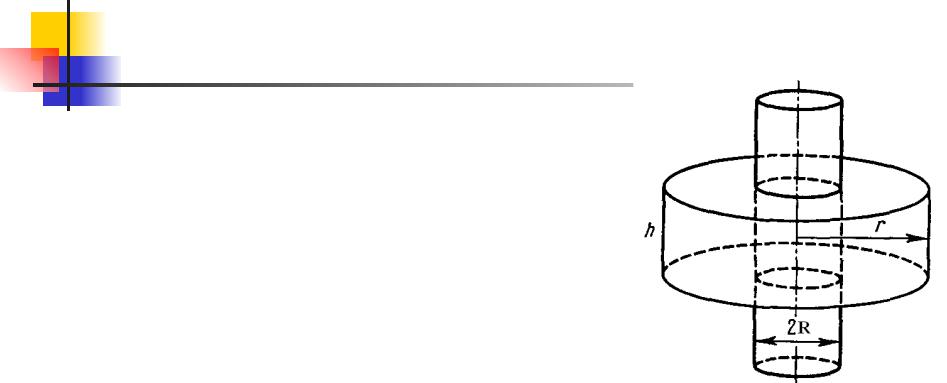
Поле бесконечного круглого цилиндра

Поле бесконечного круглого цилиндра, заряженного равномерно по поверхности так, что на единицу его длины приходится заряд λ. Из соображений симметрии следует, что вектор Е в каждой точке перпендикулярен оси цилиндра, а модуль

вектора Е зависит только от расстояния r до оси цилиндра. Это подсказывает, что замкнутую поверхность надо взять в форме

кТогдааксиального прямого цилиндра.

поток вектора Е сквозь торцы этого цилиндра равен нулю, а через боковую поверхность ЕΔS, где ΔS – площадь боковой поверхности цилиндра ΔS=2πrh. r – радиус боковой поверхности цилиндра, h – его высота. По теореме Гаусса для случая r>R (R – радиус бесконечного круглого цилиндра) имеем Е2πrh= λh/ε0,

откуда:	E
		2 0r

Электростатика. 16.9

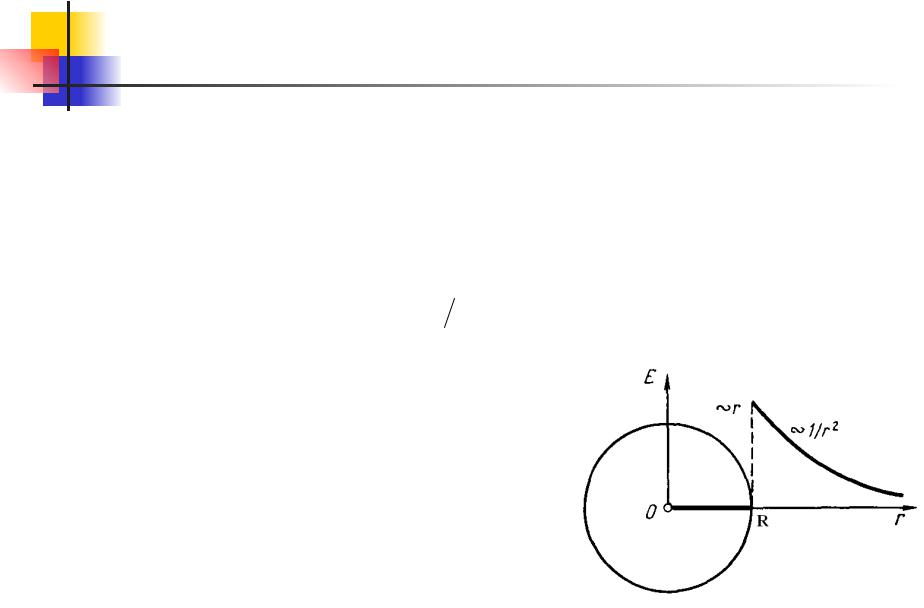
Поле сферической поверхности, заряженной равномерно зарядом q.

Это поле центрально-симметрично – направление вектора Е в любой точке проходит через центр сферы, а модуль зависит только от расстояния до центра сферы. При такой конфигурации поля в качестве замкнутой поверхности надо взять

концентрическую сферу. Пусть ееотку0 радиуса r>R, тогда по теореме
E 4 r2	q
Гаусса	E		q
			4 0r2

Если r<R, то замкнутая поверхность не содержит внутри зарядов, поэтому в этой области всюду Е=0, т.е. внутри равномерно заряженной сферической поверхности электрическое поле

отсутствует. Вне этой поверхности поле убывает с расстоянием по

такому же закону, как у точечного

заряда.

Электростатика. 16.10

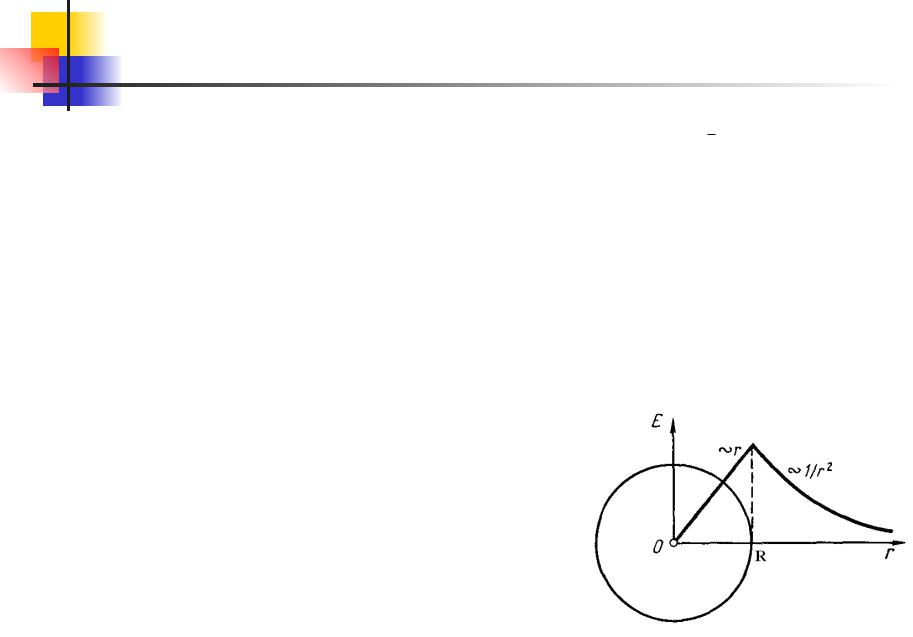
Поле сферы заряженной объемной плотностью заряда ρ

Поле такой сферы тоже обладает центральной симметрией. Для поля вне сферы получается тот же результат, что и в случае поверхностно заряженной сферы.

Однако для точек внутри результат будет другой.

4

Сферическая поверхность радиуса r (r<R) заключает в себя

3

r

3

заряд равный

довательно, теорема Гаусса для такой поверхности запишется в ви

E 4 r2

1

4 r3

0

Откуда, заменяя

чер

q

3

ρ

ез

3

получаем

4

R

3

E

1

q

r

4 0 R3

Внутри сферы напряженность поля

растет линейно с расстоянием r от центра сферы. Вне сферы

напряженность убывает по такому же

Лекция 17 Работа сил электростатического поля. Потенциал.

Эквипотенциальные поверхности. Связь между напряженностью электрического поля и потенциалом.

При перемещении пробного заряда q в электрическом поле электрические силы совершают работу. Оказывается, что работа сил

электростатического поля при перемещении заряда из одной точки

поля в другую не зависит от формы траектории, а определяется

только положением начальной и конечной точек и величиной заряда. Из механики известно, что такое поле называется консервативным. Если в качестве пробного заряда, переносимого из точки 1 в точку 2 поля Е, взять единичный положительный заряд, то элементарная работа сил поля на перемещении dl равна Edl, а вся работа сил поля на пути от точки 1 до точки 2 определяется как

2 Edl

1

Этот интеграл берется по некоторому пути (линии), поэтому его называют линейным.

Электростатика. 17.2

Интеграл данного вида, взятый по замкнутому пути, называется циркуляцией вектора Е и обозначаетсяÑ

Теорема о циркуляции вектора Е гласит:

циркуляция вектора Е в любом электростатическом поле равна нулю т.е.

2 Edl 0

1

Поле, обладающее таким свойством, называется потенциальным. Теорема о циркуляции вектора Е позволяет сделать ряд важных выводов, практически не прибегая к расчетам. Например, линии электростатического поля не могут быть замкнутыми.

Электростатика. 17.3

Тело находящееся в потенциальном поле сил, обладает потенциальной энергией, за счет которой совершается работа силами поля. Следовательно, работа сил электростатического поля может быть представлена как разность значений потенциальной энергии, которыми обладал заряд в точках 1 и 2 поля Е. Можно утверждать, что в электростатическом поле существует некоторая скалярная функция координат φ(r), убыль которой

1 2 2 Edl

Так определенная величина φ(r) называется1 потенциалом

поляИз сопоставления. данного выражения с выражением для работы сил потенциального поля ( которая равна убыли потенциальной энергии частицы в поле) можно сказать, что потенциал – это величина, численно равная потенциальной

энергии единичного положительного заряда в данной точке поля.

Электростатика. 17.4

Потенциал какой-либо произвольной точки поля определяется с

точностью до произвольной аддитивной константы. Элементарная убыль потенциала на dl есть

d Edl

Другими словами, если известно поле E(r), то для нахождения φ

надо представить как убыль некоторой функции.

отенциал поля неподвижного точечного заряда:

	1		q		q	dr2			1 q
Edl				er dl =			d				const
			2
	4 0 r				4 0 r		4 0 r

ким образом, потенциал поля точечного заряда

1 q 4 0 r

4 0

Электростатика. 17.5

Если имеется система из N неподвижных точечных зарядов q1, q2,

…. Согласно принципу суперпозиции в любой точке поля напряженность Е=Е1+Е2+…, где Еi – напряженность поля

создаваемого отдельно зарядом q1 и т.д. Тогда можно записать

Edl (E1 E 2

....)dl E1dl E2dl ....

d 1 d 1 ...

d

Таким образом, потенциал системы неподвижных точечных заряд

	1		q
			ri
	4	0
			i

Если заряды, образующие системы, распределены непрерывно, то, каждый элементарный объем dV содержит точечный заряд ρdV, где ρ – объемная плотность заряда в месте нахождения объема dV. Тогда при вычислении потенциала можно перейти от суммирования дискретно распределенных в пространстве

зарядов к интегрированию по заряж1 еннdVому объему:

r

Электростатика. 17.6

Если заряды расположены только по поверхности S то получаем

следующее соотношение: 1 dS

4 0 r

Получили, что электрическое поле можно описывать как с помощью напряженности, так и с помощью потенциала. Следовательно, раз эти две величины описывают одно и то же

физическое явление, то между ними должна существовать

однозначная связь. d Edl Связь между φ и Е можно установить с помощью соотношения

Пусть перемещение dl параллельно оси Х, тогда dl=exdx, где ex – орт оси Х; dx – приращение координаты х. В этом случае

	Edl Eexdx Exdx
Получим	Ex
		x