За м е ч а н и е. Формула (7) справедлива при α − πk, β − πk,
α+ β − πk, а формула (8) — при α − πk, β − πk, α – β − πk (k Ý Z).
6.Форм лы двойно(о ар( мента
1°. sin 2α = 2 sin α cos α, cos 2α = cos2 α – sin2 α,
tg 2α = |
----2-----tg---------α---- . |
|
1 – tg2 α |
2°. 1 |
– cos 2α = 2 sin2 α, |
|
(4) |
1 |
+ cos 2α = 2 cos2 α. |
|
(5) |
3°. Кроме перечисленных выше формул (1)—(5), полезно знать |
и формулы |
|
|
|
sin 3α = 3 sin α – 4 sin3 α, |
(6) |
|
cos 3α = 4 cos3 α – 3 cos α, |
(7) |
|
tg 3α = |
3 tg α – tg3 α |
(8) |
|
----------------------------------- . |
|
|
1 – 3 tg2 α |
|
7. Преобразование произведения три(онометричес их ф н ций в с мм
1°. sin α sin β = |
cos-----------(--α-----–------β---)----–----cos-----------(--α-----+------β---) |
, |
|
2 |
|
2°. cos α cos β = |
cos-----------(--α-----+------β---)----+----cos-----------(--α-----–------β---) |
, |
|
2 |
|
3°. sin α cos β = |
--sin---------(--α-----+------β)-------+----sin-----------(--α-----–----β----) |
, |
|
2 |
|
4°. tg α tg β = |
----tg-------α-----+------tg-------β---- |
, |
|
ctg α + ctg β |
|
|
5°. ctg α ctg β = ctg-----------α-----+------ctg---------β-- . |
(5) |
|
tg α + tg β |
|
|
З а м е ч а н и е. Формулы (4) и (5) справедливы при α − |
π----k-- , |
|
|
2 |
β − |
π----k-- (k Ý Z). Кроме то#о, в формуле (4) должно быть ctg α + |
|
2 |
|
+ ctg β − 0, а в формуле (5) tg α + tg β − 0.
8.Форм лы с ммы и разности одноименных три(онометричес их ф н ций
1°. Формулы суммы и разности синусов: |
|
|
sin α + sin β = 2 sin |
α-------+----β- |
· cos |
α-------–----β- |
; |
|
2 |
|
2 |
|
sin α – sin β = 2 sin α-------–----β- |
· cos |
α-------+----β- . |
|
2 |
|
2 |
|
2°. Формулы суммы и разности осинусов: |
|
cos α + cos β = 2 cos |
α-------+----β- |
· cos |
α-------–----β- |
; |
|
2 |
|
2 |
|
cos α – cos β = –2 sin |
α-------–----β- |
· sin |
α-------+----β- . |
|
2 |
|
2 |
|
3°. Формулы суммы и разности тан#енсов: |
|
tg α + tg β = --sin---------(--α-----+------β---)- , #де α − |
--π + πk, β − --π |
+ πk, |
cos α cos β |
2 |
|
2 |
|
(1)
(2)
(3)
(4)
k Ý Z; (5)
tg α – tg β = --sin---------(--α-------–----β---)- , #де α − --π |
+ πk, β − --π + πk, k Ý Z. |
(6) |
cos α cos β |
2 |
2 |
|
4°. Формулы суммы и разности отан#енсов: |
|
ctg α + ctg β = |
--sin---------(--α-----+------β)--- |
, #де α − πk, β − πk, k Ý Z; |
(7) |
|
sin α sin β |
|
|
|
ctg α – ctg β = |
--sin---------(--β-----–----α)----- |
, #де α − πk, β − πk, k Ý Z. |
(8) |
|
sin α sin β |
|
|
|
9. Три(онометричес ие ф н ции половинно(о ар( мента
1°. sin |
x-- |
= ä |
1------–----cos-----------x- . |
|
2 |
|
2 |
2°. cos |
x-- |
= ä |
1------+----cos-----------x-- . |
|
2 |
|
2 |
3°. tg |
x-- |
= ä |
-1-----–----cos-----------x-- . |
|
2 |
|
|
1 + cos x |
4°. tg |
x-- |
= |
1----- |
--sin--------x-------- . |
|
2 |
|
+ cos x |
5°. tg |
x-- |
= 1----- |
--–----cos---------x-- . |
|
2 |
|
|
sin x |
10.Выражение три(онометричес их ф н ций через тан(енс половинно(о ар( мента
|
2 tg x-- |
|
|
1°. sin x = |
------------------2---- |
- . |
(1) |
|
1 + tg2 |
x |
|
|
-- |
|
|
|
2 |
|
|
1 – tg2 |
x |
|
|
-- |
|
2°. cos x = |
-------------------- |
--2- . |
(2) |
1tg2 x
+--
2
За м е ч а н и е. Область определения рассматриваемых фун - ций: x − π + 2πk, k Ý Z.
|
2 tg x-- |
|
|
3°. tg x = ---- |
--------------2-- |
-- . |
(3) |
1 |
– tg2 |
x |
|
-- |
|
|
|
2 |
|
1 |
– tg2 |
x |
|
-- |
|
4°. ctg x = ---- |
2-----tg---------x-- |
--2 . |
(4) |
|
|
|
|
2 |
|
|
За м е ч а н и е. Формула (3) имеет смысл при x π + πk, x π +
−-- −
2
+2πk, k Ý Z, а формула (4) при x − πk, k Ý Z.
Тема 11
1.Ф н ция y = sin x
2.Ф н ция y = cos x
3.Ф н ция y = tg x
4.Ф н ция y = ctg x
5.Нахождение периодов три(онометричес их ф н ций
6.Обратная ф н ция
7.Ф н ция y = arcsin x
8.Ф н ция y = arccos x
9.Ф н ция y = arctg x
10.Ф н ция y = arcctg x
11.Не оторые соотношения для обратных три(онометричес их ф н ций
СПРАВОЧНЫЙ МАТЕРИАЛ
1. Ф н ция y = sin x
1°. Область определения — множество всех действительных чисел.
2°. Множество значений — отрезо [–1; 1], т. е. синус — фун - ция о#раниченная.
3°. Фун ция нечетная: sin (–x) = –sin x при всех x Ý R.
4°. Фун ция периодичес ая с наименьшим положительным периодом 2π, т. е. sin (x + 2π) = sin x при всех x Ý R.
5°. sin x = 0 при x = πk, k Ý Z.
6°. sin x > 0 при всех x Ý (2πk; π + 2πk), k Ý Z.
7°. sin x < 0 при всех x Ý (π + 2πk; 2π + 2πk), k Ý Z.
|
8°. Фун ция возрастает от –1 до 1 на промежут ах |
|
π |
+ 2πk; |
|
|
|
|
–-- |
|
|
|
|
|
2 |
|
π |
|
|
|
|
|
|
+ 2πk |
, k Ý Z. |
|
-- |
|
2 |
|
|
|
|
|
|

9°. Фун ция убывает от 1 до
–1 на промежут ах |
|
|
π |
+ 2πk; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-- |
|
|
|
|
|
|
3π |
+ 2πk |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, k Ý Z. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
------ |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10°. Фун ция принимает наи- |
|
Рис. 58 |
большее значение, равное 1, в точ- |
|
|
|
|
|
|
|
π |
|
+ 2πk, k Ý Z. |
|
|
|
|
|
|
|
|
|
|
ах x = -- |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11°. Фун ция принимает наименьшее значение, равное (–1),
в точ ах x = 3π + 2πk, k Z.
------ Ý
2
12°. Графи фун ции y = sin x изображен на рис. 58.
2. Ф н ция y = cos x
1°. Область определения — множество всех действительных чисел.
2°. Множество значений — отрезо [–1; 1], т. е. осинус — фун - ция о#раниченная.
3°. Фун ция четная: cos (–x) = cos x при всех x Ý R.
4°. Фун ция периодичес ая с наименьшим положительным периодом 2π, т. е. cos (x + 2π) = cos x при всех x Ý R.
5°. cos x = 0 |
π |
|
|
|
|
|
|
при x = -- + πk, k Ý Z. |
|
|
|
2 |
|
|
|
|
|
|
6°. cos x > 0 |
при всех x Ý |
|
– |
π |
π |
+ 2πk |
, k Ý Z. |
-- |
+ 2πk; -- |
|
|
|
|
2 |
2 |
|
|
7°. cos x < 0 |
при всех x Ý |
|
π |
|
3π |
+ 2πk |
, k Ý Z. |
-- |
+ 2πk; ------ |
|
|
|
2 |
|
2 |
|
|
8°. Фун ция убывает от 1 до –1 на промежут ах [2πk; π + 2πk], k Ý Z.
9°. Фун ция возрастает от –1 до 1 на промежут ах [–π + 2πk; 2πk], k Ý Z.
10°. Фун ция принимает наи- |
|
большее значение, равное 1, в точ- |
|
ах x = 2πk, k Ý Z. |
|
11°. Фун ция принимает на- |
|
именьшее значение, равное (–1), |
|
в точ ах x = π + 2πk, k Ý Z. |
|
12°. Графи фун ции y = cos x |
|
изображен на рис. 59. |
Рис. 59 |
3. Ф н ция y = tg x
1°. Область определения — множество всех действительных чи-
π |
+ πk, k Ý Z. |
сел, роме чисел вида x = -- |
2 |
|
2°. Множество значений — вся числовая прямая, т. е. тан#енс — фун ция нео#раниченная.
3°. Фун ция нечетная: tg (–x) = –tg x при всех x из области определения.
4°. Фун ция периодичес ая с наименьшим положительным периодом π, т. е. tg (x + π) = tg x при всех x из области определения.
5°. tg x = 0 при x = πk, k Ý Z.
6°. tg x > 0 при всех x Ý |
|
|
π |
+ πk |
, k Ý Z. |
πk; -- |
|
|
|
2 |
|
|
|
7°. tg x < 0 при всех x Ý |
|
π |
+ πk; πk |
, k Ý Z. |
–-- |
|
|
2 |
|
|
|
|
8°. Фун ция возрастает на промежут ах |
π |
+ πk; |
π |
+ πk |
, |
–-- |
-- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
k Ý Z. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 60
9°. Графи фун ции y = tg x изображен на рис. 60.
4. Ф н ция y = ctg x
1°. Область определения — множество всех действительных чисел, роме чисел вида x = πk, k Ý Z.
2°. Множество значений — вся числовая прямая, т. е. отан- #енс — фун ция нео#раниченная.
3°. Фун ция нечетная: ctg (–x) = –ctg x при всех x из области определения.
4°. Фун ция периодичес ая с наименьшим положительным периодом π, т. е. ctg (x + π) = ctg x при всех x из области определения.
5°. ctg x = 0 |
π |
|
|
|
|
|
|
при x = -- + πk, k Ý Z. |
|
|
|
|
2 |
|
|
|
|
|
|
6°. ctg x > 0 |
при всех x Ý |
|
|
π |
πk |
, k Ý Z. |
πk; -- + |
|
|
|
|
2 |
|
|
|
7°. ctg x < 0 |
при всех x Ý |
|
π |
+ πk; πk |
, k Ý Z. |
–-- |
|
|
|
2 |
|
|
|
|
8°. Фун ция убывает на промежут ах (πk; π + πk), k Ý Z.
Рис. 61
9°. Графи фун ции y = ctg x изображен на рис. 61.
5. Нахождение периодов три(онометричес их ф н ций
1°. Период фун ции: а) y = sin x равен 2π; б) y = cos x равен 2π; в) y = tg x равен π; #) y = ctg x равен π.
2°. Период фун ции, представляющей собой сумму непрерывных и периодичес их фун ций, равен наименьшему ратному периодов сла#аемых, если оно существует.
6. Обратная ф н ция
1°. Пусть фун ция y = f(x) монотонна в своей области определения D(f). То#да аждому значению x Ý D(f) соответствует единственное значение y Ý E(f) и обратно, аждое значение y Ý E(f) со-

ответствует единственному x Ý D(f). Значит, в этом случае можно построить новую фун цию, определенную на E(f) и та ую, что аждому y Ý E(f) ставится в соответствие x Ý D(f), удовлетворяющее уравнению y = f(x). Эту новую фун цию называют обратной по отношению фун ции y = f(x).
2°. Для нахождения фун ции, обратной данной y = f(x), надо выразить x через y: x = g(y), а затем записать полученную фун цию в общепринятой форму y = g(x).
3°. Отметим, что если фун ции y = f(x) и y = g(x) являются взаимно обратными, то область определения фун ции f совпадает с множеством значений фун ции g и, наоборот, область определения фун ции g — с множеством значений фун ции f, т. е. D(f) = E(g) и D(g) = E(f).
4°. Графи и взаимно обратных фун ций симметричны относительно прямой y = x (рис. 62).
5°. Рассмотрим, например, фун цию y = x2, заданную на промежут е (–×; 0]. На этом промежут е фун ция убывает и принимает все значения из множества [0; +×). Следовательно, для данной фун -
ции существует обратная. Из уравнения y = x2 находим x = 
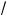 y или x = –
y или x = –
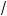 y ; та а переменная x может принимать толь о неположи-
y ; та а переменная x может принимать толь о неположи-
тельные значения, то ис омая обратная фун ция имеет вид x = – |
y . |
Поменяв обозначения x на y и y на x, получим формулу y = – |
x , |
#де x l 0, с помощью оторой и задается обратная фун ция. |
|
Если же рассматривать фун цию y = x2, заданную на промежут е [0; +×), то обратной для нее служит фун ция y = 
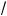 x , #де
x , #де
x l 0. На рис. 63 изображены #рафи фун ции y = x2 при x l 0 и #рафи обратной ей фун ции.
6°. Приведем дру#ие примеры взаимно обратных фун ций.
а) Фун ция f(x) = 2x на промежут е (–×; +×) возрастает и принимает все значения из множества (–×; +×). Поэтому она обрати-
x
ма. Графи и фун ции f(x) = 2x и обратной ей фун ции g(x) = --
2
изображены на рис. 64.
б) Фун ция f(x) = 4 x на промежут-е [0; +×) возрастает и принимает все значения из множества [0; +×). Значит, она обратима. Графи и фун ции
x на промежут-е [0; +×) возрастает и принимает все значения из множества [0; +×). Значит, она обратима. Графи и фун ции
f(x) = 4 x и обратной ей фун ции g(x) =
x и обратной ей фун ции g(x) =
= x4, #де x l 0, изображены на рис. 65. в) Фун ция f(x) = x3 + 1 на проме-
жут е (–×; +×) возрастает и принимает все значения из множества (–×; +×). Та им образом, фун ция f(x) обратима. Графи и фун ции f(x) = x3 + 1 и обрат-
Рис. 66
ной ей фун ции g(x) = 3 x – 1 изображены на рис. 66.
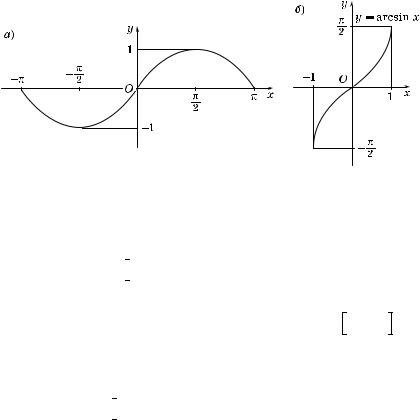
7. Ф н ция y = arcsin x
1°. Фун ция y = sin x на отрез е |
|
π |
π |
|
возрастает и прини- |
|
|
|
–-- |
; -- |
|
|
|
2 |
2 |
|
|
мает все значения из отрез а [–1; 1] (рис. 67, а). Поэтому фун ция
y = sin x на отрез е |
|
π |
π |
|
обратима, т. е. имеет обратную фун - |
|
|
–-- |
; -- |
|
|
|
2 |
2 |
|
|
Рис. 67
цию, оторую называют ар син сом и обозначают y = arcsin x. Геометричес и arcsin x означает величину у#ла (ду#и), за лючен-
но#о в промежут е |
|
π |
π |
|
, синус оторо#о равен x. |
|
|
|
–-- |
; -- |
|
|
|
2 |
2 |
|
|
2°. Графи фун ции y = arcsin x изображен на рис. 67, б. Этот
#рафи симметричен #рафи у фун ции y = sin x, x Ý
носительно прямой y = x.
3°. Отметим свойства фун ции y = arcsin x: а) D(arcsin) = [–1; 1];
б) E(arcsin) = |
|
π |
π |
|
; |
|
|
|
–-- |
; -- |
|
|
|
2 |
2 |
|
|
в) фун ция нечетная, т. е. arcsin (–x) = –arcsin x; #) фун ция возрастающая.
8. Ф н ция y = arccos x
1°. Фун ция y = cos x на отрез е [0; π] убывает и принимает все значения из отрез а [–1; 1] (рис. 68, а). Поэтому фун ция y = cos x на отрез е [0; π] обратима, т. е. имеет обратную фун цию, оторую называют ар осин сом и обозначают y = arccos x. Геометричес и arccos x означает величину у#ла (ду#и), за люченно#о в промежут-е [0; π], осинус оторо#о равен x.
2°. Графи фун ции y = arccos x изображен на рис. 68, б. Этот #рафи симметричен #рафи у фун ции y = cos x, x Ý [0; π], относительно прямой y = x.


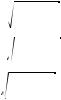






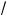 y или x = –
y или x = –
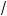 y ; та а переменная x может принимать толь о неположи-
y ; та а переменная x может принимать толь о неположи-
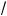 x , #де
x , #де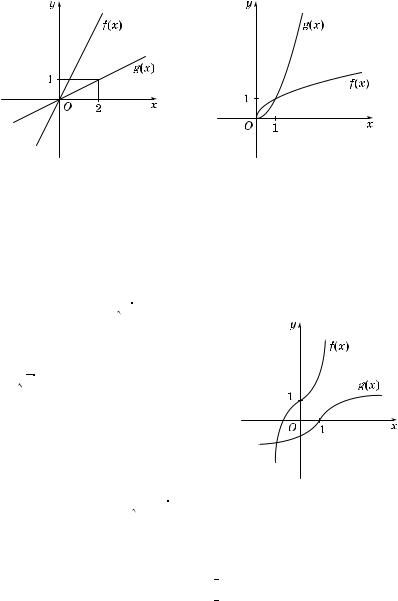
 x на промежут-е [0; +
x на промежут-е [0; + x и обратной ей фун ции g(x) =
x и обратной ей фун ции g(x) =