Задачи с параметрами и методы их решения

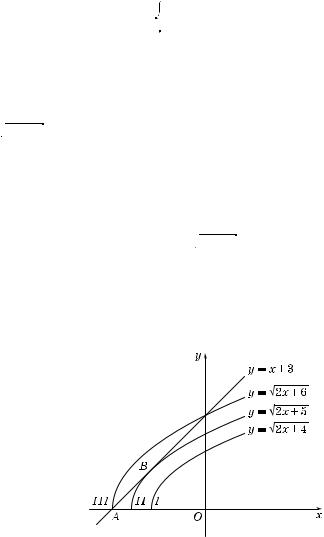
2. Приравнивая f(–2) и f′(–2) нулю, получим систему уравнений

4a – 2b = 31, –4a + b = –80,

129

решив оторую найдем a = --------- , b = 49.

4

3. Ответ: a = 32,25, b = 49.

3. Найти все значения параметра a, при оторых уравнение

2x + a = x + 3 имеет ровно один орень. В ответе у азать наименьшее целое значение a.

1.В данном случае полезно воспользоваться #рафичес ой иллюстрацией (рис. 90).

2.Графи ом фун ции y = x + 3 является прямая, пересе ающая ось абсцисс в точ е x0 = –3, а ось ординат — в точ е y0 = 3.

3.Графи ом фун ции y = 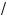2x + a для различных значений a является семейство ветвей парабол, вершины оторых находятся

вточ е –a ; 0 , а сами ветви расположены выше оси Ox.

--

2

4. На рис. 90 изображены три та ие параболы. Видно, что при увеличении a парабола смещается влево.

Рис. 90

5. Парабола I не имеет с прямой y = x + 3 общих точе , парабола II имеет с этой прямой одну общую точ у B (в оторой прямаяасается параболы) и, на онец, парабола III пересе ается с прямой y = x + 3 в двух точ ах.

251

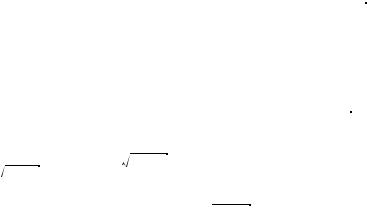
6.При дальнейшем увеличении a парабола y = 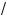2x + a будет пересе ать прямую y = x + 3 толь о в одной точ е.

7.Найдем значение параметра, соответствующее точ е A. В этой точ е имеем x0 = –3 и 2x0 + a = 0, поэтому a = 6. Значит, при a > 6

данное уравнение будет иметь ровно один орень.

8. Найдем значение параметра, соответствующее точ е B. Таа в этой точ е прямая y = x + 3 и парабола y = 2x + a асаются, то производные рассматриваемых фун ций совпадают, т. е.

2	= 1, от уда 2x + a = 1.
-- -- - -- -- -- -- -- - -- -- -- --

2 2x + a

9.Подставив это выражение в исходное уравнение, получим x + 3 = 1, от уда x = –2. Поэтому 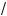– 4 + a = 1, т. е. a = 5.

10.Та им образом, a Ý (6; +×) Ÿ {5}.

11.Ответ: a = 5.

4. При а их значениях параметра a фун ция

2	– 3a + 2)		cos	2	x	– sin	2	x		+ (a – 1)x + sin 1
f(x) = (a					--			--
					4			4

не имеет ритичес их точе ?

1.Та а данная фун ция дифференцируема на всей число-

вой прямой, то ритичес ими точ ами фун ции f(x) являются те точ и, в оторых производная f′(x) = 0.

2.В данном случае имеем

1	(a – 1)(a – 2)		x		+ (a – 1).
f′(x) = --			–sin --
2			2

3.Очевидно, что если a = 1, то f′(x) = 0 при любом x Ý R, т. е. для заданной фун ции аждая точ а x Ý R является ритичес ой.

4.Предположим, что a − 1. То#да уравнение f′(x) = 0 примет

вид

x	= 2.	(1)
(a – 2) sin --
2

Отсюда следует, что если |a – 2| < 2, т. е. если a Ý (0; 1) Ÿ (1; 4), то уравнение (1) не имеет орней и, значит, при у азанных значениях a фун ция f(x) не имеет ритичес их точе .

5. Ответ: a Ý (0; 1) Ÿ (1; 4).

252

5. При а ом значении a минимум фун ции y = ax2 + 4ax + 7a2 – 1 равен 2?

1. Найдем ритичес ие точ и данной фун ции:

y′ = 2ax + 4a, y′ = 0 при x = –2.

2. В точ е x = –2 фун ция имеет э стремум, равный 2. Та им образом, f(–2) = 4a – 8a + 7a2 – 1 = 2, от уда 7a2 – 4a – 3 = 0, т. е.

3

a1 = –-- ; a2 = 1.

7

3.Мы нашли два значения a; а ое из них следует взять?

4.Та а данная фун ция имеет в ритичес ой точ е мини-

мум, то оэффициент при x2 должен быть положительным.

5.Ответ: a = 1.

6.При а ом значении a наибольшее значение фун ции y = 2x3 –

– 6x + a на отрез е [–2; 0] равно 5?

1.Выясним, имеет ли фун ция y = 2x3 – 6x + a на отрез е [–2; 0]ритичес ие точ и.

2.Производная данной фун ции y′ = 6x2 – 6 равна нулю при x = ä1.

3.Следовательно, отрез у [–2; 0] принадлежит одна ритиче- с ая точ а: x = –1.

4.Найдем значения фун ции на онцах отрез а и в ритиче- с ой точ е: y(–2) = a – 4; y(–1) = a + 4; y(0) = a.

5.Наибольшее из этих значений y(–1) = a + 4. Оно и равно 5. Следовательно, 4 + a = 5, от уда a = 1.

6.Ответ: a = 1.

7.Найти значения параметра a, при оторых произведение действительных орней уравнения

x2 + 2(a – 6)x + 2a2 – 17a + 42 = 0

принимает наибольшее значение.

1.Уравнение должно иметь орни, поэтому D l 0.

2.Находим

D	= (a – 6)2 – (2a2 – 17a + 42) = –a2 + 5a – 6 l 0,
----
4

от уда 2 m a m 3.

253

3.Со#ласно теореме Виета, имеем x1x2 = 2a2 – 17a + 42. Следовательно, задача сводится отыс анию наибольше#о значения фун ции f(a) = 2a2 – 17a + 42 на отрез е 2 m a m 3.

4.Находим ритичес ие точ и фун ции: f′(a) = 4a – 17, a =

=4,25 Ô [2; 3].

5.Значит, наибольшее значение фун ции f(a) следует ис ать на онцах отрез а [2; 3]; имеем f(2) = 16; f(3) = 9.

6.Ита , произведение орней уравнения дости#ает наибольше- #о значения при a = 2.

7.Ответ: a = 2.

8. В зависимости от значений параметра a найти наибольшее значение фун ции

f(x) =	1	(1)
	-- 2 -- ax- -- ------2---–------x----4---–------3--a-----2

на отрез е [–2; 1].

1.Дис риминант вадратно#о (относительно x2) трехчлена 2ax2 – x4 – 3a2 равен (–8a2), поэтому при любом значении параметра a и любом x из области определения фун ции f(x) ее значения отрицательны. Кроме то#о, та а f(x) = f(–x), то #рафи этой фун ции при аждом фи сированном значении a симметричен относительно оси ординат.

2.Найдем производную фун ции f(x). Имеем

f′(x) =	4x(x2 – a)
	(----2---ax--------2-----–----x---4----–------3---a----2----)-2- .	(2)

а) Если a < 0, то справедливо неравенство x2 – a > 0 и, значит, f′(x) = 0 толь о при x = 0.

б) Поэтому f′(x) < 0 при x < 0 и f′(x) > 0 при x > 0.

в) Та им образом, в точ е x = 0 фун ция f(x) имеет минимум, а наибольшее значение она принимает на левом онце данно#о отрез а, т. е. в точ е x = –2 (в силу симметрии #рафи а относительно оси ординат и то#о, что |–2| > 1).

3. Находим

1

f(–2) = –------------------------------------ .

3a2 – 8a + 16

1

4. Если a = 0, то данная фун ция примет вид f(x) = –----- ; эта x4

фун ция убывает при x < 0 и возрастает при x > 0 и, следовательно,

254

в точ е x = –2 она принимает наибольшее значение, оторое равно

– 1 .

------

16

5.Если a > 0, то производная f′(x) имеет три ритичес ие точ и: x1 = –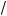a , x2 = 0, x3 = 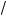a . В этом случае f′(x) < 0 при x Ý

Ý(–×; –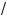a ) Ÿ (0; a ) и f′(x) > 0 при x Ý (–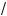a ; 0) Ÿ (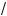a ; +×).

6.В точ е x = 0 фун ция f(x) имеет ло альный ма симум, о-

торый равен		1		. Для то#о чтобы полученное значение было
		–---------
		3a2

наибольшим, нужно, чтобы выполнялось неравенство

11

–------------------------------------ m –--------- , т. е. a l 2.

3a2 – 8a + 16 3a2

7.Ответ: если a Ý (–×; 2), то max f(x) = f(–2) = –

[–2; 1]

если a Ý [2; +×), то max f(x) = f(0) = –

[–2; 1]

1	;
3----a-----2----–-----8----a----+-----16-----
----1----- .
3a2

9. В зависимости от значений параметра t − 0 найти значения параметра a, при оторых уравнение

2x3 – 3tx2 + t = a

(1)

имеет три различных орня.

1. Для то#о чтобы уравнение (1) имело три различных орня, фун ция

f(x) = 2x3 – 3tx2 + t – a

(2)

должна иметь ло альный ма симум и ло альный минимум та ие, что f(xmax) > 0, f(xmin) < 0, #де xmax < xmin.

2. Найдем э стремумы фун ции (2). Для это#о решим уравнение

f′(x) = 6x2 – 6tx = 0.

Очевидно, что x1 = 0, x2 = t.

3. Пусть t > 0. То#да x1 < x2 и x1 — точ а ма симума, а x2 —

точ а минимума фун ции f(x). В этом случае имеем

f(x1) = t – a > 0, f(x2) = 2t3 – 3t3 + t – a = t – t3 – a < 0,

и, следовательно, t – t3 < a < t.

255

4.Пусть t < 0. То#да x2 < x1 и теперь x2 — точ а ма симума,

аx1 — точ а минимума фун ции f(x). В этом случае имеем

f(x2) = t – t3 – a > 0, f(x1) = t – a < 0

и, значит, t < a < t – t3.

5. Ответ: если t < 0, то t < a < t – t3; если t > 0, то t – t3 < a < t.

10. В зависимости от значений параметра p у азать те значения параметра k, при оторых уравнение

x3 + 2px2 + p = k

(1)

имеет три различных действительных орня.

1. Для то#о чтобы уравнение (1) имело три действительныхорня, фун ция

f(x) = x3 + 2px2 + p – k

(2)

должна иметь ло альный ма симум и ло альный минимум, причем f(xmax) > 0, а f(xmin) < 0.

2.Та а оэффициент при x3 положителен, то xmax < xmin.

3.Найдем э стремумы фун ции (2). Имеем f′(x) = 3x2 + 4px.

4p

Производная обращается в нуль при x1 = 0 и x2 = –------ .

3

4. Возможны три случая.

а) Если p > 0, то x < x и, следовательно, f(x ) = 32 p3 + p – k > 0,

2 1 2 ------

27

32p3 + 27p

а f(x1) = p – k < 0, от уда p < k < ----------------------------- .

27

б) Если p = 0, то x1 = x2 и фун ция (2) э стремумов не имеет: производная f′(x) всюду, роме x = 0, положительна и фун ция монотонно возрастает. Та им образом, в этом случае нет та их значений k, при оторых данное уравнение имело бы три действительных орня.

в) Если p < 0, то x1 < x2 и, значит, f(x1) = p – k > 0, а f(x2) =

	=	32p3	+ p – k < 0, от уда	32p3 + 27p	< k < p.
		----27--------		-------------27----------------

256

32p3 + 27p

-----------------------------

27

5. Ответ: если p < 0, то k Ý

если p = 0, то k Ý ¾; если p > 0, то k Ý p;

; p ;

32p3 + 27p

----------------------------- .

27

11. При а их отличных от нуля значениях параметров a и b все э стремумы фун ции

f(x) = a2x3 + ax2 – x + b (1) отрицательны и ло альный ма симум дости#ается в точ е x0 = –1?

1.Та а оэффициент при x3 положителен, то ма симум должен находиться левее минимума.

2.Для отыс ания э стремальных точе найдем производную фун ции (1) и приравняем ее нулю. Имеем

f′(x) = 3a2x2 + 2ax – 1 = 0,

1 1

от уда x1 = –-- , x2 = ------ . a 3a

3. Пусть a < 0; то#да	1	1	и, следовательно, x				= x		1
	------	< –--						0	= ------ ,
	3a	a				2			3a
1			1
т. е. ------ = –1. Та им образом, a = –-- .
3a			3
4. Со#ласно условию, все э стремумы отрицательны, поэтому
1	1	1
при a = –-- имеем f(–1) = – --		– -- + 1 + b < 0. Отсюда находим, что
3	9	3
5
b < –-- .
9
	1	1	, а, значит, x		= x		= –	1	, т. е.
5. Пусть a > 0; то#да – --		< ------		1		0		--
	a	3a						a
1		= 1 имеем f(–1) = –1 + 1 + 1 + b < 0 и,
–-- = –1, от уда a = 1. При a
a
следовательно, b < –1.
1		5	; при a = 1 и b < –1.
6. Ответ: при a = –--	и b < –--
3		9
12. При а их значениях параметра a уравнение
cos x +	3	2x	x
	-- cos ------		+ 3 cos -- = a
	2	3	3

имеет решения?

257

1. Рассмотрим фун цию

3 2x x f(x) = cos x + -- cos ------ + 3 cos -- ,

2 3 3

оторая является периодичес ой с наименьшим положительным периодом T = 6π.

2.Очевидно, что уравнение (1) будет иметь решения то#да и толь о то#да, о#да min f(x) m a m max f(x) на промежут е [0; 6π].

3.Для нахождения на этом промежут е ритичес их точе решим уравнение f′(x) = 0. Это уравнение имеет вид

2x	x	2x		x	+ 1		= 0.
sin x + sin ------	+ sin --	= 0, или sin ------		2 cos --
3	3	3		3

				2x				x	= –	1
		Отсюда либо sin ------ = 0, либо cos --								-- .
				3				3		2
									3π n			, n Ý Z. Второе урав-
		4. Из перво#о уравнения находим x = ----------
										2
нение дает x = ä2π + 6πk, k Ý Z.
		5. Та им образом, промежут у [0; 6π] принадлежат следующие
ритичес ие точ и фун ции f(x): x								= 0, x				3π			= 2π, x		= 3π,
							1			2	= ------ , x			3		4
												2
x			9π	= 6π.
	5	= 4π, x = ------ , x
		6	2	7
		6. Вычислив значения фун ции f(x) в этих точ ах, находим
				11	f	3π			= f	9π			3		,
			f(0) = f(6π) = ------ ,			------				------		= –--
				2		2				2			2

7.	5
	Ответ: –--
	2

5	5
f(2π) = f(4π) = –--	, f(3π) = –-- .
4	2
11
m a m ------ .
2

13. Найти множество всех чисел a, при аждом из оторых фун - ция

f(x) = sin 2x – 8(a + 1)sin x + (4a2 + 8a – 14)x

является возрастающей на всей числовой прямой и не имеет при этом ритичес их точе .

1. При любом фи сированном a данная фун ция дифференцируема в аждой точ е числовой прямой.

258

2.Та а фун ция f(x) возрастает, то в аждой точ е x должно выполняться неравенство f′(x) l 0.

3.Та а , роме то#о, f(x) не имеет ритичес их точе , то при любом x должно быть выполнено неравенство f′(x) − 0.

4.Та им образом, если фун ция удовлетворяет условию задачи, то при всех x должно быть выполнено неравенство f′(x) > 0.

5.С дру#ой стороны, если при всех x выполнено неравенство f′(x) > 0, то фун ция, очевидно, не имеет ритичес их точе и возрастает.

6.Найдем производную данной фун ции:

f′(x) = 2 cos 2x – 8(a + 1) cos x + 4a2 + 8a – 14.

Теперь задачу можно переформулировать та : найти все значения параметра a, при аждом из оторых для любо#о x выполнено неравенство

cos 2x – 4(a + 1) cos x + 2a2 + 4a – 7 > 0.

(1)

7. Учитывая, что cos 2x = 2 cos2 x – 1, и пола#ая cos x = t, #де –1 m t m 1, перепишем неравенство (1) следующим образом:

2t2 – 1 – 4(a + 1)t + 2a2 + 4a – 7 > 0,

или

t2 – 2(a + 1)t + a2 + 2a – 4 > 0.

(2)

8.Обозначив фун цию в левой части неравенства (2) через ϕ(t),

дадим новую формулиров у исходной задачи: найти все значения a, при аждом из оторых наименьшее значение фун ции ϕ(t) на от-

рез е [–1; 1] положительно.

9.Производная ϕ′(t) = 2t – 2(a + 1) обращается в нуль при t0 =

=a + 1.

10.Наименьшее значение фун ции ϕ(t) на отрез е [–1; 1] есть:

ϕ(–1) = a2 + 4a – 1, если a + 1 m –1; ϕ(a + 1) = –5, если –1 < a + 1 < 1; ϕ(1) = a2 – 5, если a + 1 l 1.

11.Та а наименьшее значение фун ции ϕ(t) на отрез е [–1; 1] должно быть положительно, то значения параметра a, удовлетворяющие условию задачи, принадлежат двум промежут ам: a m –2

иa l 0.

12.Если a m –2, то ис омые значения параметра a удовлетворя-

ют неравенству a2 + 4a – 1 > 0.

259

13.Если a l 0, то ис омые значения параметра a удовлетворяют неравенству a2 – 5 > 0.

14.Следовательно, множество ис омых значений a есть объединение решений двух систем неравенств:

	a m –2,		(3)
	a2	+ 4a – 1 > 0;

	a l 0,			(4)
	a2	– 5	> 0.

15.Множество решений системы (3) есть промежуто –× < a <

<–2 – 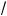5 , а множество решений системы (4) — промежуто a > 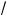5 .

16.Ответ: a Ý (–×; –2 – 5 ) Ÿ (5 ; +×).

14.Прямая y = 5x + 3 асается параболы y = x2 + bx + c в точ е A(–2; –7). Найти b и c.

1.Находим производную y′ = 2x + b и ее значение y′(–2) = –4 + b,оторое равно у#ловому оэффициенту k = 5 асательной параболе в точ е A.

2.Та им образом, –4 + b = 5, от уда b = 9.

3.Значение c найдем из условия, что точ а A(–2; –7) лежит на параболе. Имеем –7 = 4 + 9(–2) + c, от уда c = 7.

4.Ответ: b = 9, c = 7.

15.Известно, что парабола y = ax2 + bx + 1 асается прямой y = = 7x – 2 в точ е M(1; 5). Найти значение выражения 4a – b2.

1.Найдем производную фун ции y = ax2 + bx + 1:

y′ = (ax2 + bx + 1)′ = 2ax + b.

2. Та а M(1; 5) — точ а асания, то x0 = 1, y0 = 5. Следовательно, 5 = a · 1 + b · 1 + 1 и 2a + b = 7.

3. Составим и решим систему уравнений

5 = a + b + 1, 2a + b = 7,

от уда a = 3, b = 1.

4. Ответ: 11.

260