Задачи с параметрами и методы их решения

Рис. 79

Рис. 78

5. Решить неравенство tg x > a.

1. Построим единичную о ружность и проведем ось тан#енсов, оторая являетсяасательной о ружности в точ е A(1; 0) (рис. 78).

2.На оси тан#енсов находим точ у C, ордината оторой равна a.

3.Точ а пересечения отрез а OC с о -

ружностью есть онец ду#и AP, тан#енс оторой равен a.

4. Из рис. 78 видно, что данному неравенству удовлетворяют все ду#и, началом оторых является точ а P, а онцом — любая внутренняя точ а ду#и PB, т. е.

		π
	arctg a < x < -- .
		2
5.	Используя периодичность тан#енса, запишем ответ.
6.	π	+ πk, k Ý Z.
	Ответ: arctg a + πk < x < --
	2

6. Решить неравенство ctg x > a.

1. Построим единичную о ружность и проведем ось отан#енсов, являющуюся асательной о ружности в точ е B(0; 1) (рис. 79).

2.На оси отан#енсов возьмем точ у C, абсцисса оторой равна a.

3.Точ а пересечения отрез а OC с о -

ружностью есть онец ду#и AP, отан- #енс оторой равен a.

4. Из рис. 79 видно, что данному неравенству удовлетворяют все ду#и, началом оторых является точ а A, а онцом — любая внутренняя точ а ду#и AP, т. е.

0 < x < arcctg a.

5.Учитывая периодичность отан#енса, запишем ответ.

6.Ответ: πk < x < arcctg a + πk.

З а м е ч а н и е. Задачи 3—6 можно та же решить #рафиче- с и, используя #рафи и соответствующих три#онометричес их фун ций.

231

7. В зависимости от значений параметра a решить неравенство

1

sin ax m –-- .

2

1. На единичной о ружности находим две точ и, ординаты о-

1

(рис. 80).

торых равны –--

2

2. Одна из этих точе является онцом

аждой из ду# множества arcsin

1

+ 2πk =

–--

2

π

+ 2πk, а дру#ая — онцом аждой из

= –--

6

ду# множества –π – arcsin

1

+ 2πk = –π +

–--

2

π

5π

+ -- + 2πk = –------ + 2πk, k Ý Z.

6

6

				3. Из рис. 80 видно, что данное неравен-
Рис. 80			ство справедливо, о#да
					5π					π
					–------ + 2πk m ax m –-- + 2πk, k Ý Z.
					6					6
4. а) Отсюда при a > 0 получим
1		5	π		m x m	1		π	+ 2πk		, k Ý Z.
--		–------ + 2πk				--		–--
a		6				a		6
б) При a < 0 находим
1		π	+ 2πk		1			5π	+ 2πk		, k Ý Z.
--		–--			m x m --		–------
a		6			a			6

в) При a = 0 решений нет.

5. Ответ: если a = 0, то решений нет;

1		5	π	+ 2πk		m x m	1		π	+ 2πk	;
если a > 0, то --		–------					--		–--
a		6					a		6
1		π	+ 2πk			1			5π	+ 2πk	,
если a < 0, то --		–--			m x m --			–------
a		6				a			6

k Ý Z.

8. В зависимости от значений параметра a решить неравенство sin ax < b, #де 0 < b < 1.

232

1.Построим на единичной о ружности две точ и с ординатой, равной b.

2.Данное неравенство справедливо, о#да

–π – arcsin b + 2πk < ax < arcsin b + 2πk, k Ý Z.

3. а) Отсюда при a > 0 находим

1	(π(2k – 1) – arcsin b) < x <				1	(arcsin b + 2πk), k Ý Z.
--					--
a					a
б) При a < 0 находим
1	(arcsin b + 2πk) < x			1
--				< -- (π(2k – 1) – arcsin b), k Ý Z.
a				a
в) Если a = 0, то x — любое действительное число.
4. Ответ: если a = 0, то x Ý R;
	если a > 0, то
	1					1			+ 2πk);
	-- (π(2k			– 1) – arcsin b) < x < -- (arcsin b
	a					a
	если a < 0, то
	1					1
	-- (arcsin b + 2πk) < x < -- (π(2k – 1) – arcsin b),
	a					a
									k Ý Z.
				π		2
9. Решить неравенство cos ax – --						m –------- .
				4		2
1. На единичной о ружности найдем две точ и, абсциссы ото-
	2
рых равны –------- (рис. 81).
	2
2. Данное неравенство верно, о#да
3π		–	π	5π
------ + 2πk m ax			-- m	------ + 2πk,
4			4	4
т. е.
π		3π
	+ 2πk m ax m ------ + 2πk, k Ý Z.
		2
3. а) Отсюда при a > 0 находим
1	1		3π
-- (π + 2πk) m x m --			------ + 2πk , k Ý Z.
a	a		2					Рис. 81

233

б) При a < 0 находим

1		3π		1	(π + 2πk), k Ý Z.
--		------ + 2πk		m x m --
a		2		a

в) При a = 0 решений нет.

4. Ответ: если a = 0, то решений нет;

1				1		3π		;
если a > 0, то --	(π + 2πk) m x m --					------ + 2πk
a				a		2
1		3π		m x <		1
если a < 0, то --		------ + 2πk				-- (π + 2πk), k Ý Z.
a		2				a

10. В зависимости от значений параметра a решить неравенство

tg(ax + 2) l

3 .

1. На оси тан#енсов находим точ у C, ордината оторой

равна 3 (рис. 82).

2. Точ а пересечения отрез а OC с о руж-

π

ностью является онцом ду#и -- .

3

3. Пос оль у период тан#енса равен π, за-

лючаем, что данное неравенство справедли-

во при

π

π

+ πk,

-- +

πk m ax + 2 < --

3

2

Рис. 82

или

π

+

π

+ πk, k Ý Z.

–2 + --

πk m ax < –2 + --

3

2

4. а) Отсюда при a > 0 имеем

1

π

– 2 + πk

m x <

1

π

– 2 + πk

, k Ý Z.

--

--

--

--

a

3

a

2

б) При a < 0 получим

1

π

– 2 + πk

< x m

1

π

– 2 + πk

, k Ý Z.

--

--

--

--

a

2

a

3

в) Если a = 0, то неравенство примет вид tg 2 l 3 , что неверно. Следовательно, при a = 0 оно не имеет решений.

234

5. Ответ: если a = 0, то решений нет;

1		π	– 2 + πk	1		π	– 2 + πk ;
если a > 0, то --		--		m x < --		--
a		3		a		2
1		π	– 2 + πk	1		π	– 2 + πk ,
если a < 0, то --		--		< x m --		--
a		2		a		3
							k Ý Z.

11. В зависимости от значений параметра m решить неравенство

ctg (mx – 1) m 2.

1. На оси отан#енсов находим точ у C, абсцисса оторой равна 2 (рис. 83).

2. Точ а пересечения отрез а OC с о - ружностью есть онец ду#и arcctg 2.

3. Та а период отан#енса равен π, то приходим выводу, что данное неравенство верно при

arcctg 2 + πk m mx – 1 < π + πk,

или

Рис. 83

1+ arcctg 2 + πk m mx < 1 + π + πk.

4.а) Отсюда при m > 0 находим

1	1	(1 + π + πk), k Ý Z.
----	(1 + arcctg 2 + πk) m x < ----
m	m

б) При m < 0 получим

1	1	(1 + arcctg 2 + πk), k Ý Z.
----	(1 + π + πk) < x m ----
m	m

в) При m = 0 неравенство примет вид ctg (–1) m 2, что верно. Значит, при m = 0 неравенство справедливо для любых x.

5. Ответ: если m = 0, то x Ý R; если m > 0, то

1	1	(1 + π + πk);
----	(1 + arcctg 2 + πk) m x < ----
m	m

если m < 0, то

1	1	(1 + arcctg 2 + πk), k Ý Z.
----	(1 + π + πk) < x m ----
m	m

235

12. В зависимости от значений параметра a решить неравенство

(a – 2) sin x > 3a + 4.

(1)

1.Очевидно, что при a = 2 неравенство (1) не имеет решений.

2.Будем считать, что a – 2 − 0. При та их значениях параметра a рассмотрим сначала случай a – 2 < 0. В этом случае неравенст-

3a + 4

во (1) равносильно неравенству sin x < ---------------- . a – 2

То#да при выполнении условий

a – 2 < 0,

3a + 4

---------------- m –1, a – 2

1

т. е. при –-- m a < 2, неравенство (1) не имеет решений.

2

3. Если же выполняются условия

a – 2 < 0,

3a + 4

---------------- > 1, a – 2

т. е. если a < –3, то решением неравенства (1) является любое x. 4. Далее, если

			a – 2 < 0,
			–1 < 3a + 4 m 1,
			a – 2
--т. е. если –3 m a < –1		, то неравенство (1) имеет следующие реше-
	2
ния:
–arcsin 3----a-----+------4-	+ π(2k – 1) < x < arcsin			3----a-----–------4-	+ 2πk, k Ý Z.
a – 2				a – 2
5. Рассмотрим теперь случай a – 2 > 0. В этом случае 3----a-----+------4-						> 1,
					a – 2

апотому неравенство (1) не имеет решений.

6.Ответ: если a < –3, то x Ý R;

если –3 m a < –			1--	, то –arcsin 3----a-----+------4- + π(2k – 1) < x <
			2	a – 2
				< arcsin 3----a-----+------4-	+ 2πk, k Ý Z;
				a – 2
если a l –	1--	, то решений нет.
	2

236

13. При а их значениях параметра a неравенство

a(4 – sin x)4 – 3 + cos2 x + a > 0

(1)

справедливо для любых значений x?

1.	Пос оль у неравенство (1) должно выполняться при всех
значениях переменной x, оно должно выполняться и при x =		π
		-- .
		2
При этом значении x из неравенства (1) следует, что 82a – 3 > 0.
2.	Та им образом, все значения параметра a, удовлетворяющие
	3
требованию задачи, принадлежат промежут у a > ------ .
	82

3. Замечая теперь, что при любом значении переменной x справедливы неравенства cos2 x l 0, 4 – sin x l 3, (4 – sin x)4 l 81 и при этом a > 0, получим

a(4 – sin x)4 – 3 + cos2 x + a l 81a – 3 + a = 82a – 3 > 0.

4.						3	удовлетворяют
	Ита , все значения a из промежут а a > ------
						82
требованию задачи.
5.	Ответ: a Ý		3	; +×		.
			------
			82
14. При а их значениях параметра a вадратное уравнение
				8x2 + 8x cos a + 1 = 0			(1)

не имеет действительных орней?

1. Найдем дис риминант уравнения (1):

D = (8 cos a)2 – 4 · 8 = 32(2 cos2 a – 1).

Если он отрицателен, т. е. если

2 cos2 a – 1 < 0,

(2)

то вадратное уравнение (1) не имеет действительных орней.

2. Неравенство (2) равносильно неравенству cos 2a < 0, решивоторое получим ответ.

3.	π	3π
	Ответ: --	+ πk < a < ------ + πk, k Ý Z.
	4	4

237

15. При а их значениях параметра a неравенство

a2 + 2a – sin2 x – 2a cos x > 2

справедливо для любо#о x?

1. Та а sin2 x = 1 – cos2 x и множество значений фун ции y = cos x есть промежуто [–1; 1], то задачу можно переформулировать та : при а их значениях параметра a наименьшее значениевадратно#о трехчлена

f(y) = y2 – 2ay + a2 + 2a – 3

(1)

на отрез е –1 m y m 1 положительно?

2. В силу то#о, что абсцисса вершины параболы (1) равна a, за-лючаем, что наименьшее значение фун ции (1) на отрез е [–1; 1] есть:

f(–1) = a2 + 4a – 2, f(a) = 2a – 3,

f(1) = a2 – 2,

если a m –1; если –1 < a < 1; если a l 1.

3. Учитывая, что наименьшее значение фун ции f(y) должно быть положительным, приходим сово упности следующих систем неравенств:

a2 + 4a – 2 > 0, a m –1;

2a – 3 > 0, –1 < a < 1;

a2 – 2 > 0, a l 1.

(2)

(3)

(4)

4. Решение системы (2) есть промежуто –× < a < –2 – 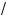6 , система (3) несовместна, а решение системы (4) — промежуто

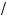2 < a < +×.

5.Ответ: a Ý (–×; –2 – 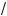6 ) Ÿ (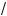2 ; +×).

16.При а их значениях параметра k неравенство

sin6 x + cos6 x + k sin x cos x l 0

(1)

справедливо для всех значений x?

238

1. Преобразуем левую часть неравенства (1). Имеем

sin6 x + cos6 x + k sin x cos x = (sin2 x)3 + (cos2 x)3 + k sin x cos x = = (sin2 x + cos2 x)((sin2 x + cos2 x)2 – 3 sin2 x cos2 x) + k sin x cos x =

3 k

=1 – sin 2x. (2)

2.Используя подстанов у y = sin 2x, сведем неравенство (2)

равносильному неравенствуsin2 2x + --2--4

3	y2	k	y + 1 l 0.	(3)
–--		+ --
4		2

3. Теперь задачу можно переформулировать та : при а их значениях параметра k неравенство (3) справедливо для всех y из промежут а [–1; 1]?

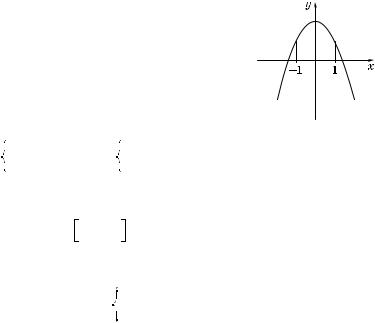
4. Обозначим вадратный трехчлен в левой части неравенства (3) через f(y). Та а ветви параболы, соответствующей этому трехчлену, направлены вниз (рис. 84), то требование задачи выполняется, если совместна система

Рис. 84

	f(–1) l 0,	или		1	– 2k l 0,
	f(1) l 0,			1	+ 2k l 0.
					1	1
Решив последнюю систему, находим –--						m k m -- .
					2	2

1 1

5.Ответ: k Ý – .

17.При а их значениях a и b система неравенств-- ; --2 2

a + sin bx m 1,	(1)
x2 + ax + 1 m 0	(2)

имеет единственное решение?

1.Необходимым условием существования единственно#о решения данной системы является равенство нулю дис риминанта D =

=a2 – 4 вадратно#о трехчлена в левой части неравенства (2).

2.Та им образом, требуемыми значениями параметра a мо#ут быть толь о a = –2 и a = 2.

3.Если a = –2, то x = 1, а неравенство (1) примет вид sin b m 3 и, следовательно, b — любое число.

239

240

4.	Если a = 2, то x = –1, а неравенство (1) примет вид sin b l 1.
		π	+ 2πk, k Ý Z.
Решением это#о неравенства являются значения b = --
		2
5.	π	+ 2πk, k Ý Z.
	Ответ: a = –2, b Ý R; a = 2, b = --
	2

ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ

1. В зависимости от значений параметра a решить неравенство: а) sin x > a (–1 < a < 0); б) cos x l a (0 < a < 1);

в) sin				π		3
			ax – --			< –------- ;
				4		2
д) tg	π			– ax		3
		--				< ------- ;
	8					3

2. Решить неравенство:

2	x	+ a sin	2	1	;
а) sin	--			x l --
	2			2

в) 0 m cos x m 4 – a2;

#) cos		π	– ax				1	;
		--				m --
		3					2
е) ctg		ax +		2π			l	3
				------				------- .
				5				3
			1			m a;
б) cos x – -------------
			cos x
#) sin2 x + -------				1------	--		l a.
			sin2 x

3. Найти значения параметра a, при оторых для всех x Ý R выполняется неравенство:

а) sin 2x + (a + 1)	2	sin		π		< 2a;
				x – --
				4

б) sin2 x – (a + 1) sin 2x + 2a + 3 > 0; в) cos2 x + (a + 1) sin x < 2 + 3a.

4. Найти все значения a, при оторых неравенство

5 5 a2 – 11

sin x + cos x – a(sin x + cos x) l ------------------ (sin x + cos x) sin x cos x

2

π

верно для всех x та их, что 0 m x m -- .

4

Ответы

1. а) arcsin a + 2πk < x < π – arcsin a + 2πk; б) 2πk – arccos a m x m 2πk +

+ arccos a; в) если a = 0, то решений нет; если a > 0, то

1--

2πk – 5------π

< x <

a

12

< 1--

2πk –

------π

; если a < 0, то

1--

2πk –

------π

< x <

1--

2πk –

5------π ; ) если

a

12

a

12

a

12