Задачи с параметрами и методы их решения

ности, оно верно при x = π и x = 2π. Поэтому числа a и b удовлетворяют равенствам

–2a + b2 = cos (πa + b2) – 1,	(2)
b2 = cos (2πa + b2) – 1.	(3)

2.Та а cos (2πa + b2) m 1, то из равенства (3) следует, что b2 m 0. Этому условию удовлетворяет толь о b = 0; то#да cos 2πa =

=1, т. е. a — целое число.

3.При b = 0 равенство (2) примет вид 1 – 2a = cos πa. Но –1 m m cos πa m 1, от уда –1 m 1 – 2a m 1, т. е. 0 m a m 1. В промежут е 0 m a m 1 имеются толь о два целых числа: a = 0 и a = 1.

4.Ита , условию задачи мо#ут удовлетворять толь о следующие пары чисел: а) a = 0, b = 0; б) a = 1, b = 0.

5.Если a = 0, b = 0, то равенство (1), очевидно, выполняется при всех x.

6.Если a = 1, b = 0, то равенство (1) та же выполняется при всех x.

7.Следовательно, обе пары чисел a = 0, b = 0 и a = 1, b = 0 удовлетворяют условию задачи.

8.Ответ: (0; 0); (1; 0).

30. При а их значениях параметра a уравнение

(x2 + 9) cos ax = 2(x2 – 3x + 9)

(1)

имеет решения? Найти эти решения.

1. Уравнение (1) равносильно уравнению

	cos ax =	2(x2	– 3x + 9)		,	(2)
		-------------x---2----		+------9------------

правая часть оторо#о положительна при всех x и в силу неравенства |cos ax| m 1 не превосходит единицы.

2. Решив неравенство

2(x2 – 3x + 9)

-------------------------------------- m 1, x2 + 9

за лючаем, что равенство (2) возможно лишь при x cos 3a = 1.

3. Отсюда следует, что 3a = 2πk, k Ý Z, т. е. a =

2π k

4. Ответ: если a = ---------- , k Ý Z, то x = 3.

3

= 3, т. е. о#да

2π k

---------- , k Ý Z.

3

221

31. В зависимости от значений параметра a решить уравнение

x2 + 4x cos ax + 4 = 0.

(1)

1. Перепишем уравнение (1) следующим образом:

(x + 2 cos ax)2 + 4(1 – cos2 ax) = 0.

(2)

2. Оба сла#аемых в левой части уравнения (2) неотрицательны. Следовательно, это уравнение равносильно системе

x + 2 cos ax = 0, 1 – cos2 ax = 0,

или, что то же самое, сово упности двух систем:

x + 2 cos ax = 0, cos ax = 1;

x + 2 cos ax = 0, cos ax = –1.

3. Решив систему (3), находим x = –2, a = πn, n Ý Z.

4.		π	+ πk, k Ý Z.
	Решив систему (4), получим x = 2, a = --
		2
5.	π	+ πk, k Ý Z, то x = 2;
	Ответ: если a = --
	2

если a = πn, n Ý Z, то x = –2;

при дру#их a уравнение не имеет решений.

(3)

(4)

32. В зависимости от значений параметра a определить число орней уравнения

sin4 x – cos4 x = a(tg4 x – ctg4 x),						(1)
принадлежащих интервалу		0;	π	.
			--
			2
1. Перепишем уравнение (1) в виде
				sin8 x – cos8 x	,
sin4 x – cos4 x = a--------------------------------------
				sin4 x cos4 x
или
(sin4 x – cos4 x)[sin4 x cos4 x – a(sin4 x + cos4 x)] = 0.						(2)

222

2. Уравнение (2) равносильно сово упности двух уравнений:

sin4 x – cos4 x = 0,	(3)
sin4 x cos4 x – a(sin4 x + cos4 x) = 0.	(4)

3. Уравнение (3) при любом значении параметра a имеет на ин-

тервале		0;	π		π
			--		орень x = -- .
			2		4

4. Уравнение (4) в результате преобразований приводится виду

sin4 2x + 8a sin2 2x – 16a = 0.

(5)

Пола#ая y = sin2 2x, получим уравнение

y2 + 8ay – 16a = 0,

(6)

оторое имеет действительные орни, если е#о дис риминант D = = 64(a2 + a) l 0, т. е. если a l 0 или если a m –1.

При та их значениях a орнями уравнения (6) являются

y1 = 4(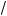a(a + 1) – a), y2 = –4(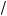a(a + 1) + a).

5.Пусть a > 0. То#да y2 < 0 и толь о орень y1 уравнения (6) может дать решения уравнения (5).

6.Учитывая, что речь идет об интервале 0; π , приходим не-

--2

равенству

					0 < 4( a(a + 1) – a) < 1,
			1		. При та их значениях a уравнение (5) имеет на
от уда 0 < a < --
			8
интервале		0;	π		два орня.
			--
			2
7. При a =			1		получим y		= 1, поэтому уравнение (5) имеет на
			--			1
			8
интервале		0;	π				π
			--		толь о один орень x = -- .
			2				4
8. При a >			1	уравнение (5) решений не имеет.
			--
			8

9. При a = 0 на интервале		0;	π		уравнение (5) та же не имеет
			--
			2

решений.

223

10. Если a m –1, то нетрудно убедиться, что орни y1 и y2 не удовлетворяют условиям 0 < y1 < 1, 0 < y2 < 1, и, следовательно, уравнение (5) снова не имеет решений.

11.	Ответ: если a Ý (–×; 0]	Ÿ		1	; +×		, то один орень;
				--
				8

если a Ý 0; 1--8 , то три орня.

33. При а их значениях параметра a уравнения
2 sin7 x – (1 – a) sin3 x + (2a3 – 2a – 1) sin x = 0	(1)
и
2 sin6 x + cos 2x = 1 + a – 2a3 + a cos2 x	(2)

равносильны?

1.Заметим, что x = π — орень уравнения (1) при любом a. То#- да со#ласно условию это значение должно быть и орнем уравнения (2).

2.Подставляя x = π в уравнение (2), получаем равенство a3 = a. Отсюда следует, что ис омые значения параметра a мо#ут принадлежать толь о множеству {0; –1; 1}.

3.Пусть a = 0. То#да уравнения (1) и (2) перепишутся соответственно в виде

sin x(sin2 x – 1)(2 sin4 x + 2 sin2 x + 1) = 0,

и

sin2 x (sin2 x – 1)(sin2 x + 1) = 0.

Та а

2 sin4 x + 2 sin2 x + 1 − 0 и sin x + 1 − 0,

то при a = 0 уравнения (1) и (2) равносильны. 4. Пусть a = –1. То#да получим уравнения

sin x (2 sin6 x – 2 sin2 x – 1) = 0 и sin2 x (2 sin4 x – 3) = 0,оторые, а и в предыдущем случае, равносильны, пос оль у

2 sin6 x – 2 sin2 x – 1 = 2 sin2 x (sin4 x – 1) – 1 < 0, 2 sin4 x – 3 < 0.

224

Та им образом, и при a = –1 уравнения (1) и (2) равносильны. 5. Пусть a = 1. То#да уравнения (1) и (2) примут соответственно

вид

sin x (2 sin6 x – 1) = 0, sin2 x (2 sin4 x – 1) = 0.

1

Следовательно, с одной стороны, sin x = 6 -- , а с дру#ой sin x =

2

1

= 4 -- . Поэтому при a = 1 уравнения (1) и (2) не равносильны.

2

6. Ответ: a Ý {0; –1}.

ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ

1. Найти все значения a, при оторых имеет решение данное уравнение:

а) cos2 x + 6 sin x = 4a2 – 2; б) 5 sin x + 2 cos x = a;

в) a cos x – 2 sin x =		2 + 2 – a .
2. Решить относительно x уравнение:
а) a sin2 x + cos x = 0;
б) cos x – sin x = a;
		a	;
в) sin (a + x) + sin x = cos --
		2
#) sin (x + a) + cos (x + a) = sin (x – a) + cos (x – a);
д) sin4 x – 2 cos2 x + a2 = 0;
	a
е) cos6 x – sin6 x = -- cos 2x;
	8
sin x – 1	sin x – 2
ж) ----------------------	+ a = ---------------------- .
sin x – 2	sin x	– 3

3.	Найти орни уравнения |cos 2x| = |sin2 x – a|, удовлетворяю-
щие условию 0 m x m 2π.
4.				2		– sin2 x	= a имеет на от-
	При а их значениях a уравнение -------------------------
				1		+ sin x
рез е [0; 2π] ровно один орень?
5.	Решить систему уравнений:
а)		sin x + sin y = a,	б)		cos x – cos y = a,
		π			2π
		x + y = -- ;			x + y = ------ .
		2			3

225

Ответы

1. а) |a| m	2 ; б) |a| m 29 ; в) a Ý [ 5		– 1; 2]. 2. а) Если a − 0, то x =
= äarccos 1--------------------------------–	1 + 4a2-	+ 2πn; если a = 0, то x =		--π	+ πn; б) если a Ý [– 2 ;		2 ],
	2a			2
то x = – --π ä arccos ------a-		+ 2πn; если a Ô [–	2 ;		2 ], то x Ý ¾; в) если a = π +
4	2
+ 2πk, то x Ý R; если a Ô π + 2πk, то x = –			a	+ (–1)		n π	= πk,
			2--			-- + πn; ) если a
						6

то x Ý R; если a − πk, то x = --π															+ πk; д) если a Ý (–×; – 2 ) Ÿ (													2 ; +×), то
														4
x Ý ¾; если a = ä 2 , то x = πk; если a Ý (–																			2 ;	2 ), то x = ä1--								arccos (3 –
																									2
– 2 3 – a2 ) + πk; е) если a Ý (–×; 6] Ÿ [8; +×), то x = π------n +																									--π ; если a Ý (6; 8),
																						2			4
то x1 =			π n	+	π , x2 =							π n ä 1			arccos (a – 7); ж) если a Ý												1 ;	1				, то x =
			2		4							2		4													12	2
		n	arcsin			5	–	1				1 +		4	+	πn; если		a Ô			1	;	1		, то орней нет.
= (–1)						--		--						--a							------		--
						2		2													12		2
3.	1--	arccos		1----------------– 2a , π ä							1--		arccos 1 – 2a , 2π –----------------					1--	arccos 1 – 2a----------------								( де –1 m a m 2);
	2				3						2					3		2					3
1	arccos (2a – 1), π							ä	1			arccos (2a – 1), 2π –						1	arccos (2a – 1) ( де 0 m a m 1).
--									--									--
2									2									2
4. a = 0,5. 5. а) Если a Ý (–×; –																2 ) Ÿ (	2 ; +×), то решений нет; если a =
= –		2 , то x = 3----π--						+ 2πk, y = – --π								– 2πk; если a Ý (–							2 ;				2 ), то x					1	= --π +
						4									4																		4
+ arccos a---------				2- + 2πk, y						1		= --π		– arccos a---------2- – 2πk, x						2	= --π		– arccos a-----						----2- + 2πk,
			2										4			2						4							2
y2 =		π	+ arccos				a	2			– 2πk; если a =						2 , то x =				π		+ 2πk, y =						π				– 2πk;
		4--					-----2-----														--								--
																					4								4
б) если a Ý (–×; –								3 ) Ÿ ( 3 ; +×), то решений нет; если a = –																					3 , то x =
=	5----π--	– 2πk, y = – --π										+ 2πk; если a Ý (–						3 ;		3 ), то x = π +(–1)k + 1 ×--
	6							6																	3
× arcsin a---------				3-	+		π----k--	, y =					--π	+ (–1)k arcsin a----				-3----	3- +	π-- k----		; если a =							3 , то x =
			3				2						3								2
= – --π		– 2πk, y =					5----π--	+ 2πk.
	6						6

226

Тема 13

1.Решение три(онометричес их неравенств вида sin x > a, sin x < a

2.Решение три(онометричес их неравенств вида cos x > a, cos x < a

3.Решение три(онометричес их неравенств вида tg x > a, tg x < a

СПРАВОЧНЫЙ МАТЕРИАЛ

1.Решение три(онометричес их неравенств вида sin x > a, sin x < a

1°. Неравенства, содержащие переменную толь о под зна-ом три#онометричес ой фун ции, называют три онометриче- с ими.

2°. При решении три#онометричес их неравенств используют свойство монотонности три#онометричес их фун ций, а та же промежут и их зна опостоянства.

3°. Для решения простейших три#онометричес их неравенств вида sin x > a, sin x < a используют единичную о ружность или #ра-

фи фун ции y = sin x. 4°. Важно знать, что:

sin x = 0, если x = πk, k Ý Z;

sin x = –1, если x = –π + 2πk, k Z;

-- Ý

2

π	+ 2πk, k Ý Z;
sin x = 1, если x = --
2

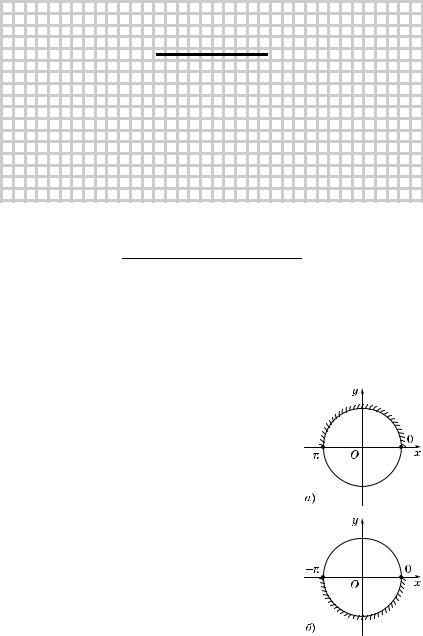
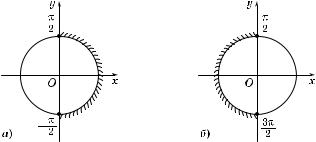
sin x > 0, если 2πk < x < π + 2πk, k Ý Z
(рис. 72, а);
sin x < 0, если –π + 2πk < x < 2πk, k Ý Z
(рис. 72, б).	Рис. 72

227

2.Решение три(онометричес их неравенств вида cos x > a, cos x < a

1°. Для решения простейших три#онометричес их неравенств вида cos x > a, cos x < a используют единичную о ружность или #рафи фун ции y = cos x.

2°. Важно знать, что:

π	+ πk, k Ý Z;
cos x = 0, если x = --
2

cos x = –1, если x = π + 2πk, k Ý Z; cos x = 1, если x = 2πk, k Ý Z;

		π	π	+ 2πk, k Ý Z (рис. 73, а);
cos x > 0, если 2πk – --			< x < --
2			2
		π	3π
cos x < 0, если 2πk + --			< x < ------ + 2πk, k Ý Z (рис. 73, б).
2			2

Рис. 73

3.Решение три(онометричес их неравенств вида tg x > a, tg x < a

1°. Для решения простейших три#онометричес их неравенств вида tg x > a, tg x < a используют единичную о ружность или #рафи фун ции y = tg x.

2°. Важно знать, что:

	π	+ πk, k Ý Z (рис. 74, а);
tg x > 0, если πk < x < --
	2
π	< x < πk, k Ý Z (рис. 74, б);
tg x < 0, если πk – --
2

π	+ πk, k Ý Z.
тан#енс не существует, если x = --
2

228

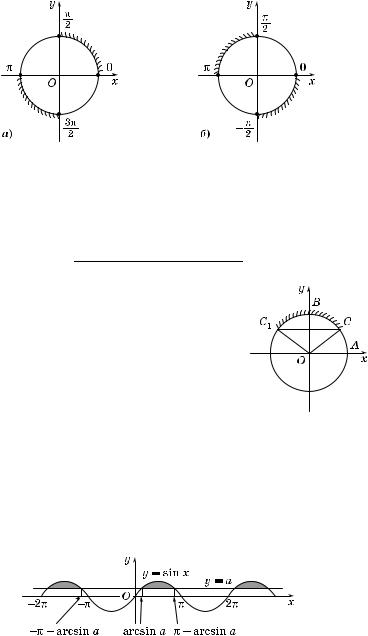
Рис. 74

З а м е ч а н и е. Неравенства ctg x > 0 и ctg x < 0 выполняются на тех же интервалах, что и неравенства tg x > 0 и tg x < 0.

ЗАДАЧИ С РЕШЕНИЯМИ

1. Решить неравенство sin x > a, #де 0 < a < 1.

I способ. 1. На единичной о ружности построим ду#и AC и AC1, синус оторых равен a (рис. 75).

2. Из рисун а видно, что данному неравенству удовлетворяют все ду#и, началом о- торых является точ а C, а онцом — любая внутренняя точ а ду#и CBC1, т. е.

Рис. 75

arcsin a < x < π – arcsin a.

3.Чтобы получить все решения данно#о неравенства, достаточно прибавить онцам это#о промежут а 2πk, k Ý Z.

4.Ответ: arcsin a + 2πk < x < π – arcsin a + 2πk, k Ý Z.

IIспособ. 1. Построим #рафи фун ции y = sin x и прямую y =

=a (рис. 76).

Рис. 76

229

2.На рисун е отмечены нес оль о промежут ов значений x,

удовлетворяющих данному неравенству; одним из них является (arcsin a; π – arcsin a).

3.Используя периодичность синуса, запишем ответ.

2.Решить неравенство sin x < a, #де 0 < a < 1.

1.Используя рис. 75, за лючаем, что данному неравенству удовлетворяют все ду#и, началом оторых является точ а C1,

а онцом — любая внутренняя точ а ду#и C1AC, т. е.

–π – arcsin a < x < arcsin a.

2.Чтобы получить все решения данно#о неравенства, прибавим онцам это#о промежут а 2πk, k Ý Z.

3.Ответ: –π – arcsin a + 2πk < x < arcsin a + 2πk, k Ý Z.

4.Тот же результат получится, если рассмотреть #рафи фун - ции y = sin x и прямую y = a (см. рис. 76), а затем отметить те промежут и, на оторых синусоида лежит ниже прямой y = a.

3.Решить неравенство cos x > a, #де –1 < a < 0.

1.На единичной о ружности построим ду#и AC и AC1, осинус

оторых равен a (рис. 77).

2. Из рисун а видно, что данному неравенству удовлетворяют все ду#и, началом о- торых является точ а C1, а онцом — любая

	внутренняя точ а ду#и C1AC, т. е.
	–arccos a < x < arccos a.
	3. Учитывая периодичность осинуса, за-
	пишем ответ.
	4. Ответ: –arccos a + 2πk < x < arccos a +
Рис. 77	+ 2πk, k Ý Z.

4. Решить неравенство cos x < a, #де –1 < a < 0.

1. Используя рис. 77, за лючаем, что данному неравенству удовлетворяют все ду#и, началом оторых является точ а C, а онцом — любая внутренняя точ а ду#и CA1C1, т. е.

arccos a < x < 2π – arccos a.

2.Учитывая периодичность осинуса, запишем ответ.

3.Ответ: arccos a + 2πk < x < 2π – arccos a + 2πk, k Ý Z.

230