
Задачи с параметрами и методы их решения
.pdf

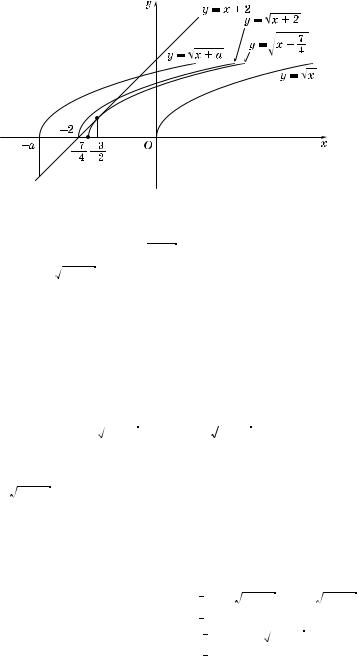
Рис. 95 |
2. Рассмотрим уравнение 
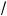 x + a = x + 2, т. е. x2 + 3x + 4 – a = 0.
x + a = x + 2, т. е. x2 + 3x + 4 – a = 0.
Имеем x = |
–----3-------ä----------- |
4----a-----–----7- , #де a l |
7-- |
. При a = |
7-- |
уравнение имеет один |
|
2 |
|
4 |
|
4 |
|
орень x = –3-- . Это соответствует случаю асания параболы и прямой. |
|||||||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3. При a < |
7-- |
неравенство не имеет решений. |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4. Если a > |
7-- |
, но a m 2, то парабола пересе ает прямую в двух |
||||||||||||||||||
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
точ ах; данное неравенство справедливо при |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
–-----3------–---------4----a-----–----7- |
|
m x m – 3 + 4a – 7 .---------------------------------- |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||
|
5. При a > 2 парабола пересе ает прямую толь о в одной точ е |
||||||||||||||||||||
x |
= –-----3------+---------4----a-----–----7- и данное неравенство выполняется на отрез е [–a; x ]. |
||||||||||||||||||||
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
||
|
6. Ответ: если a Ý |
|
–×; |
7 |
, то решений нет; |
|
|
|
|
|
|
|
|
||||||||
|
|
4-- |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
если a = |
7-- |
, то x = –3-- ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
4 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
если a Ý |
|
7 |
|
, то x Ý |
|
|
|
– 3 – 4a – 7 |
; |
– 3 + 4a – 7 |
|
|
; |
|||||||
|
|
|
|
|
|||||||||||||||||
|
|
-- ; 2 |
|
|
2------------------------------- |
--- |
----------- 2----------------------- |
|
|
|
|||||||||||
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|||||||
|
если a Ý (2; +×), то x Ý |
|
–a; – 3 + |
4a – 7 |
|
. |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
293 |
|||


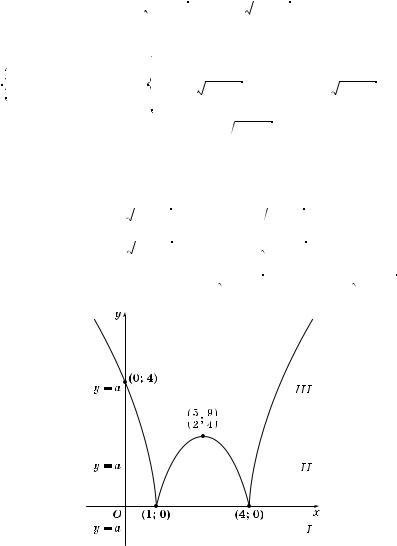





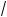 4 – x
4 – x
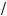 x + a
x + a 
 x + a с вершиной в точ е (–a; 0).
x + a с вершиной в точ е (–a; 0).
 ax < 3a – x, т. е. x
ax < 3a – x, т. е. x
 9 + 4a ) < x < 1 при всех a > 0 есть решение неравенства (1).
9 + 4a ) < x < 1 при всех a > 0 есть решение неравенства (1).


 x + 2
x + 2
 x – 1 –
x – 1 – 
 x + 3 – 4
x + 3 – 4
 x – 1 = a.
x – 1 = a. 4 – x
4 – x
 x + a
x + a 
 x
x
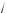 3 + a ; в) если a m 0, то нет орней; если a > 0,
3 + a ; в) если a m 0, то нет орней; если a > 0,
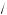 4a + 1 ); если a > 0, то x = 0,5(2a + 1 +
4a + 1 ); если a > 0, то x = 0,5(2a + 1 + 
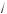 4a + 1 ); б) если a Ý (–×; 0) Ÿ (0,5; +×), то нет орней; если a Ý [0; 0,5], то x = 0,5(1 – a –
4a + 1 ); б) если a Ý (–×; 0) Ÿ (0,5; +×), то нет орней; если a Ý [0; 0,5], то x = 0,5(1 – a – 
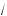 2a – 3a
2a – 3a
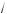 2 , то нет орней; если |a| = 0,5
2 , то нет орней; если |a| = 0,5
 2 , то x = 0,5; если 0,5
2 , то x = 0,5; если 0,5
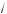 2 < |a| m 1,
2 < |a| m 1,
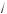 2 ; +×), то нет орней; если a Ý [–2; 2) Ÿ {2
2 ; +×), то нет орней; если a Ý [–2; 2) Ÿ {2
 2 }, то один орень;
2 }, то один орень;
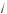 2 )a m x m 2a; в) если 2 < a m 4, то –a m x <
2 )a m x m 2a; в) если 2 < a m 4, то –a m x <
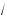 4a – a
4a – a
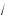 4a – a
4a – a
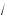 5 – a
5 – a
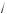 5 , то –0,4(
5 , то –0,4(
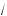 5 – a
5 – a
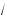 5 – a
5 – a
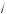 5 , то решений нет; д) если a m 0,75, то решений нет; если a = 0,75, то x = –0,5; если 0,75 < a m 1, то –0,5(1 +
5 , то решений нет; д) если a m 0,75, то решений нет; если a = 0,75, то x = –0,5; если 0,75 < a m 1, то –0,5(1 + 
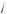 4a – 3 ) m m x m 0,5(
4a – 3 ) m m x m 0,5(
 4a – 3 – 1); если a > 1, то –a m x m 0,5(
4a – 3 – 1); если a > 1, то –a m x m 0,5(
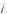 4a – 3 – 1). 6. a Ý (–2,25; 2).
4a – 3 – 1). 6. a Ý (–2,25; 2).