6.Если у#ловые оэффициенты прямых (4) и (5) различны,
т.е. a − –2b, то система (1), (2) будет иметь решения при любом b − 0.
7.Если же a = –2b, то система (1), (2) будет иметь решения то#- да и толь о то#да, о#да прямая (4) расположена ниже прямой (5),
7
т. е. о#да -- < –1, от уда следует, что –7 < b < 0. b
8.Ответ: a − 0, b = 0; a − –2b, b − 0; a = –2b, –7 < b < 0.
18.Найти все значения a, при оторых система
 (x2 + 1)a + (b2 + 1)y = 2,
(x2 + 1)a + (b2 + 1)y = 2,

 a + bxy + x2y = 1 (1)
a + bxy + x2y = 1 (1)
имеет хотя бы одно решение для любо#о значения b (a, b, x, y — действительные числа).
1.Та а система (1) должна иметь хотя бы одно решение для любо#о b, то она должна иметь решение и для b = 0.
2.Если b = 0, то система (1) примет вид
(x2 + 1)a + 1y = 2, |
(2) |
a + x2y = 1. |
(3) |
3.Уравнение (2) удовлетворяется либо при a = 0 и любом x, либо при x = 0 и любом a.
4.При x = 0 из уравнения (3) следует, что a = 1.
5.Та им образом, возможны толь о два значения a: a = 0 и a = 1.
6.Пусть a = 0; то#да система (1) примет вид
(b2 + 1)y = 1, |
(4) |
bxy + x2y = 1. |
(5) |
7.Уравнение (4) имеет решение для любо#о b толь о если y = 0. Одна о это значение не удовлетворяет уравнению (5).
8.Пусть a = 1; то#да система (1) примет вид
 x2 + (b2 + 1)y = 1,
x2 + (b2 + 1)y = 1,

 bxy + x2y = 0. (6)
bxy + x2y = 0. (6)
9.Очевидно, что система (6) для любо#о значения b имеет решение x = 0, y = 0.
10.Ответ: a = 1.



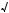

 4 tg
4 tg
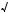


 (3) 3
(3) 3

 2
2 –3u + 4v = a + 3.
–3u + 4v = a + 3.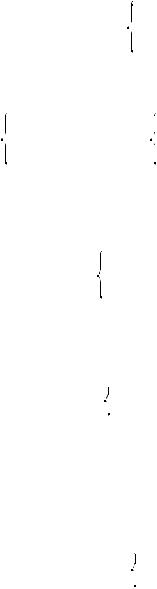
 –3u + 5v = 16 + 11a.
–3u + 5v = 16 + 11a. 5
5

 (x
(x
 a + bxy + x
a + bxy + x x
x
 bxy + x
bxy + x