Задачи с параметрами и методы их решения

Тема 3

1.Уравнения с одной переменной

2.Понятие о равносильности равнений

3.Свойства числовых равенств и теоремы о равносильностиравнений

4.Линейное равнение с одной переменной, содержащее параметр

СПРАВОЧНЫЙ МАТЕРИАЛ

1. Уравнения с одной переменной

1°. Пусть заданы фун ции f(x) и ϕ(x). Если относительно равенства f(x) = ϕ(x) поставлена задача найти все значения переменной, при оторых получается верное числовое равенство, то #оворят, что задано равнение с одной переменной.

2°. Значение переменной, обращающее уравнение в истинное равенство, называют орнем равнения.

3°. Решить уравнение — значит найти множество е#о орней или до азать, что их нет. Это множество называют та же решением равнения.

4°. Множество всех x, при оторых одновременно имеют смысл выражения f(x) и ϕ(x), называют областью определения равнения.

5°. Для то#о чтобы установить область определения уравнения, необходимо найти пересечение множеств, на оторых определены данные фун ции f(x) и ϕ(x).

2. Понятие о равносильности равнений

1°. Два уравнения называют равносильными (или э вивалентными) на данном числовом множестве, если аждое решение ( о- рень) одно#о уравнения является решением ( орнем) дру#о#о, и наоборот.

2°. Заметим, что если оба уравнения не имеют решений на данном числовом множестве, то их та же считают равносильными на этом множестве.

21

3°. Например, уравнения x2 + 3 = 0 и x4 + 2 = 0 равносильны на множестве действительных чисел, та а множество решенийаждо#о из них пустое.

3.Свойства числовых равенств и теоремы о равносильностиравнений

1°. Числовое равенство не нарушится, если обеим е#о частям прибавить или отнять одно и то же число.

2°. Если обеим частям уравнения f(x) = ϕ(x) прибавить одну и ту же фун цию A(x), имеющую смысл при всех допустимых значениях переменной, то получится новое уравнение f(x) + A(x) = = ϕ(x) + A(x), равносильное данному.

3°. Любое сла#аемое можно перенести из одной части уравнения в дру#ую, изменив зна это#о сла#аемо#о на противоположный.

4°. Числовое равенство не нарушится, если обе е#о части умножить или разделить на одно и то же число, отличное от нуля.

5°. Если обе части уравнения f(x) = ϕ(x) умножить (или разделить) на одну и ту же фун цию A(x) − 0, имеющую смысл для любо#о x из области определения, то получится новое уравнение

f(x)	ϕ(x)	, равносильное данному.
A(x) · f(x) = A(x) · ϕ(x) или ------------	= ------------
A(x)	A(x)

4. Линейное равнение с одной переменной, содержащее параметр

1°. Пусть дано уравнение вида
f(a, b, c, ... , k, x) = ϕ(a, b, c, ... , k, x),	(1)

#де a, b, c, ... , k, x — переменные величины.

2°. Переменные a, b, c, ... , k, оторые при решении уравнения

(1) считаются постоянными, называют параметрами, а само уравнение называют равнением, содержащим параметры.

3°. Решить уравнение (1) — значит у азать, при а их значениях параметров существуют значения x, удовлетворяющие данному уравнению.

З а м е ч а н и я.

1. В дальнейшем уравнение

F(x, a) = 0

(2)

условимся понимать не а уравнение с двумя переменными, а а уравнение с одной переменной x и одним параметром a.

22

2.Решить уравнение (2) — это значит решить (на множестве действительных чисел) семейство уравнений, оторые получаются из уравнения (2) при различных действительных значениях параметра a.

3.При решении уравнения с параметром (параметрами) стремятся выделить «особые» значения параметра (ино#да их называют « онтрольными»), в оторых или при переходе через оторые происходит ачественное изменение уравнения.

ЗАДАЧИ С РЕШЕНИЯМИ

1.В зависимости от значений параметра a решить уравнение ax = 0.

1.Это уравнение содержит параметр a (переменную, оторая в условии данно#о примера сохраняет одно и то же значение).

2.а) Пусть a = 0; то#да 0 · x = 0, т. е. x Ý R.

0

б) Пусть a − 0; то#да x = -- = 0. a

3.Ответ: если a = 0, то x Ý R; если a − 0, то x = 0.

2.В зависимости от значений параметра a решить уравнение ax = a.

1.Данное уравнение содержит параметр a.

2.а) Пусть a = 0; то#да 0 · x = 0, т. е. x Ý R.

a

б) Пусть a − 0; то#да x = -- = 1. a

3. Ответ: если a = 0, то x Ý R; если a − 0, то x = 1.

3. В зависимости от значений параметра a решить уравнение

x + 2 = ax.

(1)

1.Данное уравнение содержит параметр a.

2.После упрощения уравнение (1) примет вид x – ax = –2, т. е.

x(1 – a) = –2.

(2)

3.а) Пусть 1 – a = 0, т. е. a = 1; то#да получим уравнение x · 0 =

=–2, оторое не имеет орней.

б) Пусть 1 – a − 0, т. е. a − 1; то#да уравнение (2) имеет единст-

венный орень x =	-----2-------	.
	a – 1

23

4. Ответ: если a = 1, то нет орней;
если a − 1, то единственный орень x =	-----2-------	.
	a – 1

З а м е ч а н и е. Ка понимать выражение: «уравнение имеет единственный орень»?

Это означает, что аждому допустимому значению a соответствует единственное значение x.

Например, если a = 0, то x = –2; если a = 2, то x = 2 и т. д.

4. В зависимости от значений параметра a решить уравнение
(a2 – 1)x = 2a2 + a – 3.	(1)
1. Приведем уравнение (1) виду
(a – 1)(a + 1)x = (2a + 3)(a – 1).	(2)

2. а) Пусть a = 1; то#да уравнение (2) примет вид 0 · x = 0. Е#о решением является любое действительное число, т. е. x Ý R.

б) Пусть a = –1; то#да уравнение (2) примет вид 0 · x = –2. Это уравнение не имеет решений.

в) Пусть a − –1 и a − 1; то#да уравнение (2) имеет единственное решение

2a + 3
x = ---------------- .
a + 1
3. Ответ: если a = 1, то x Ý R;
если a = –1, то нет орней;
если a − –1, a − 1, то x =	2----a-----+------3- .
	a + 1
5. Решить уравнение
2a(a – 2)x = a – 2.		(1)

1.Пусть a = 0; то#да уравнение (1) примет вид 0 · x = –2. Это уравнение не имеет решений.

2.Пусть a = 2; то#да уравнение (1) примет вид 0 · x = 0. Корнем это#о уравнения служит любое действительное число.

3.Пусть a − 0 и a − 2; то#да из уравнения (1) следует, что x =

=	-------a------–---2--------	, от уда находим x =	--1---- .
	2a(a – 2)		2a

24

4. Ответ: если a = 0, то орней нет; если a = 2, то x Ý R;

1

если a − 0, a − 2, то x = ------ .

2a

6. В зависимости от значений параметра a решить уравнение

a + x	= 0.
x----2-----–----5-----x----–-----6-

1.По смыслу уравнения должно быть x2 – 5x – 6 − 0, т. е. x − –1,

x − 6.

2.При x − –1 и x − 6 данное уравнение имеет решение x = –a.

3.Из условий x − –1 и x − 6 следует, что a − 1 и a − –6.

4.Ответ: если a − –6, a − 1, то x = –a;

если a = –6, a = 1, то x Ý ¾.

7. При а их значениях параметра b уравнение

ax – b = 2a + 3x

(1)

имеет решение для любо#о a?

1. Преобразуем уравнение (1) виду

(a – 3)x = b + 2a.

(2)

2. Пусть a − 3; то#да уравнение (2) имеет решение

b+ 2a x = ----------------

a – 3

при любом значении b.

3. Следовательно, единственным значением a, при отором мо- #ут отсутствовать решения уравнения (2), является a = 3. В этом случае уравнение (2) примет вид

0 · x = b + 6.

(3)

4.Если b − –6, то уравнение (3) не имеет решений. Если же b =

=–6, то любое x Ý R есть решение уравнения (3).

5.Ита , b = –6 есть единственное значение параметра b, приотором уравнение (2) имеет решение для любо#о a (а именно, x = 2 для a − 3 и x Ý R для a = 3).

6.Ответ: b = –6.

25

8. В зависимости от значений параметра k решить уравнение

---------3----kx---------–----5---------	+	3----k-----–------11----	=	2----x-------+----7- .	(1)
(k – 1)(x + 3)		k – 1		x + 3

1.По смыслу уравнения должно быть (k – 1)(x + 3) − 0, т. е. k − 1, x − –3.

2.Упростив уравнение (1), получим

3kx – 5 + (3k –11)(x + 3) = (2x + 7)(k – 1),
или
(4k – 9)x = 31 – 2k.		(2)
9	находим
3. Из уравнения (2) при k − --
4

31– 2k x = ------------------- .

4k – 9

4.Теперь проверим, существуют ли та ие k, при оторых найденное значение x равно (–3). Имеем

	31---------–------2---k-	= – 3,
	4k – 9
от уда k = –2-- .
5
5. Та им образом, при k − 1, k − 9-- , k − –				2--	уравнение (1) имеет
		4		5
единственное решение x =	31---------–------2---k-	; при k =	9--	и при k = –		2--	решений
	4k – 9		4			5

нет; при k = 1 уравнение не имеет смысла.

6. Ответ: если k − –	2--	, k − 1, k −			9--	, то x =	31---------–------2---k-	;
	5				4		4k – 9
если k = –	2--	или k =	9--	, то орней нет;
	5		4

если k = 1, то уравнение не имеет смысла.

З а м е ч а н и я.

1. Необходимо иметь в виду, что если при а ом-либо значении параметра k = k0 данное уравнение не имеет смысла, то, разумеется, нет и е#о решения при k = k0.

26

2. Обратное утверждение неверно. Например, нельзя утверждать,

что при k = –2--	рассмотренное выше уравнение не имеет смысла.
5
3. Подставив в уравнение (1) значение k = –				2--	, получим
				5
	--6---x------+----25------	+ 61------	= 2----x-------+----7- .		(3)
	7(x + 3)	7	x + 3
Та им образом, при k = –		2-- уравнение (1) имеет смысл. Одна о
		5

это уравнение не имеет орней, та а орень x = –3 уравнения 53x = –159, оторому сводится уравнение (3), является для не#о посторонним.

9. Решить относительно x уравнение

a2	+ x	–	a2 – x		=	4abx + 2a2 – 2b2		(1)
--b--2-----	------		--b--2-----	------		---------------b---4----	------------------------ .
	– x			+ x			– x2

1.По смыслу уравнения x − äb2.

2.Та а b4 – x2 − 0, то, умножив обе части уравнения (1) на b4 – x2, получим

(a – b)2x = a2 – b2.

(2)

3.Пусть a = b; то#да уравнение (2) примет вид 0 · x = 0, т. е. оно удовлетворяется при любом действительном значении x, роме x = äb2.

4.Пусть a − b; то#да уравнение (2) примет вид

		x =	a2 – b2	=	a + b	.
			(----a-----–----b---)--2-		--a-----–----b-
5. Найдем теперь те значения a и b, при оторых выполняются
равенства a-------+----b-		= b2 и a-----+------b- = –b2:
	a – b	a – b
а) a-----+------b-	= b2; a + b = ab2 – b3, от уда a = b----(---b----2----+-----1---) ;
a – b						b2 – 1
б) a-------+----b-	= –b2; a + b = –ab2 + b3, от уда a = b----(---b----2----–---1-----) .
a – b						b2 + 1

27

	6. Ответ: если a − b, a		b(b2		+ 1)		b(b2 – 1)		, то x =	a + b	;
			− ---------	----	–-----1-----	, a − ------------------		1-----		------------
			b2				b2 +			a – b
	если a = b, то x Ý R, роме x = äb2;
	если a =	b(b2	+ 1)	или a =			b(b2 – 1)	, то орней нет.
		-----b----2----	–-----1-----				----b-----2----+-----1-----
	10. Найти значения параметра m, при оторых уравнение
	m2x – m2 + 6 = 4x + m										(1)

а) имеет единственное решение; б) не имеет решений;

в) имеет бес онечное множество решений.

1. Приведем уравнение (1) виду

(m2 – 4)x = m2 + m – 6.

(2)

2.Уравнение (2) имеет единственное решение, если m2 – 4 − 0,

т.е. если m − ä2.

3.Уравнение (2) не имеет решений, если выполнены условия

m2	– 4 = 0,	т. е.		m = ä2,	от уда m = –2.
m2	+ m – 6 − 0,			m − 2; m − –3,

4.Уравнение (2) имеет бес онечное множество решений, если

иоэффициент при x, и правая часть одновременно равны нулю:

m2	– 4 = 0,	т. е.		m = ä2,	от уда m = 2.
m2	+ m – 6 = 0,			m = 2; m = –3,

5. Ответ: а) m Ý (–×; –2) Ÿ (–2; 2) Ÿ (2; +×); б) m = –2; в) m = 2.

11. В зависимости от значений параметра k решить уравнение

2		1
kx---------+------2-	=	2----x-------+----k- .	(1)

1.Допустимыми значениями x и k являются те, при оторых kx + 2 − 0 и 2x + k − 0, т. е. kx − –2 и 2x − –k.

2.Упростив уравнение (1) при допустимых значениях k и x, получим 4x + 2k = kx + 2, или

(k – 4)x = 2(k – 1).

(2)

28

2(k – 1)

-------------------- ; k – 4

3. Пусть k = 4; то#да уравнение (2) не имеет решений.

Пусть k − 4; то#да x =		2----(---k------–---1----) .
		k – 4
4. Ис лючим теперь значения k, при оторых kx = – 2 и 2x = –k.
а) kx = –2, т. е. 2k(k –----------------------1--) = –2 или
	k – 4
	k2 – k = –k + 4,
	k − 4,	от уда k = ä2, k − 4.
б) Эти же значения k получим, решив уравнение 2x = –k. Дей-
ствительно, 2x = –k, т. е.		4----(---k------–---1----) = – k или
		k – 4

	4k – 4 = –k2 + 4k,		от уда k = ä2, k − 4.
	k	− 4,

5. Ответ: если k − ä2, k − 4, то x =

если k Ý {ä2; 4}, то x Ý ¾.

12. В зависимости от значений параметров a и b решить уравнение

ax – 1	b	a(x2 + 1)	= 0.	(1)
----------------	+ ------------	– ------------------------
x – 1	x + 1	x2 – 1

1.Уравнение имеет смысл при всех x − ä1.

2.С учетом ОДЗ преобразуем уравнение (1) в равносильное:

	(ax – 1)(x + 1) + b(x – 1) = a(x2 + 1),
или
	x(a + b – 1) = a + b + 1.	(2)
3.	а) Пусть a + b = 1; то#да уравнение (2) не имеет решений.
	a + b + 1
б) Пусть a + b − 1; то#да x = ---------------------- .
	a + b – 1
4.	Из условия x − –1 следует, что a + b + 1 − –(a + b – 1), т. е.
a + b − 0.
5.	Равенство x = 1, т. е. a + b + 1 = a + b – 1, не выполняется ни
при а их значениях a и b.
6.	a + b + 1	;
	Ответ: если a + b − 0, a + b − 1, то x = ----------------------
	a + b – 1

если a + b = 0 или a + b = 1, то x Ý ¾.

29

13. В зависимости от значений параметра a решить уравнение

a-----+------2----x-	= 1.	(1)
1 + ax

1. В области определения данно#о уравнения, т. е. при 1 + ax − 0, имеем

a-------+----2----x-----–----1-----–----ax------	= 0, или (2 – a)x = 1 – a.	(2)
1 + ax

Полученное уравнение (2) — линейное.

2. Если оэффициент при неизвестном в линейном уравнении отличен от нуля, то уравнение имеет орень и притом единственный.

Значит, если a − 2, то уравнение (2) имеет единственный о-

1 – a

рень x = ------------ . При этом для исходно#о уравнения (1) должно вы-

2 – a

полняться условие 1 + ax − 0, т. е.

1 – a

1 + a · ------------ − 0, от уда a − ä 2 .

2 – a

3. Если оэффициент при неизвестном в линейном уравнении равен нулю, а свободный член не равен нулю, то уравнение не имеет орней.

Этот случай для уравнения (2) реализуется при a = 2. Следовательно, исходное уравнение (1) при a = 2 и при a = ä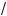2 не имееторней.

4.Если оэффициент при неизвестном и свободный член в линейном уравнении равны нулю, то уравнение имеет бес онечное множество орней.

Последний случай для уравнения (2) не имеет места ни при а-их a.

5.Ответ: если a − 2, a − ä2 , то уравнение имеет единствен-

1 – a

ный орень x = ------------ ;

2 – a

если a = 2 или a = ä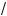2 , то уравнение не имеет орней.

14. При а их значениях a уравнения x2 – a = 0 и 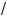x – a = 0 равносильны?

1. Если a > 0, то первое уравнение имеет два орня, а второе — толь о один, и в этом случае о равносильности речь идти не может.

30