Задачи с параметрами и методы их решения

2.Если a = 0, то решения уравнений совпадают.

3.Если a < 0, то ни первое, ни второе уравнения решений не имеют. Ка известно, та ие уравнения считаются равносильными.

4.Ответ: a m 0.

15.Определить, при а их значениях параметра a уравнения

x2 + ax + 1 = 0,		(1)
x2 + x + a = 0		(2)
имеют: а) один общий орень; б) два общих орня.
1. Пусть x1 — общий орень уравнений (1) и (2), т. е.
x2	+ ax + 1 = 0,	(3)
1	1
x12	+ x1 + a = 0.	(4)

То#да из равенства (4) следует, что a = –x21 – x1. Подставив это выражение в равенство (3), получим

x21 – x1(x21 + x1) + 1 = 0, или x31 = 1,

от уда x1 = 1 и, следовательно, a = –2.

2.Провер ой убеждаемся, что при a = – 2 уравнения (1) и (2) имеют один общий орень x = 1.

3.Пусть уравнения (1) и (2) имеют два общих орня. Это имеет место то#да и толь о то#да, о#да оэффициенты уравнений (1) и (2) пропорциональны:

1	a	1	,
--	= --	= --
1	1	a

т.е. о#да a = 1.

4.При a = 1 уравнения (1) и (2) сводятся одному уравнению

x2 + x + 1 = 0. Это уравнение не имеет действительных орней, т. е. значение a = 1 не удовлетворяет условию задачи.

5. Ответ: а) один общий орень при a = –2;

б) нет двух общих орней ни при а их a.

31

16. При а их a уравнение ax = a2 равносильно неравенству |x – 3| l a?

1.Если a − 0, то уравнение ax = a2 имеет единственное решение x = a, а неравенство |x – 3| l a — бес онечное множество решений.

2.Если a = 0, то решением а неравенства, та и уравнения является множество всех действительных чисел.

3.Та им образом, требованию задачи удовлетворяет толь о

a = 0.

4.Ответ: a = 0.

ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ

1. Решить уравнение:
а)	-------a-----	= 2; б) a-------+----5-	= a; в) a2x – a = 4x + 2;
	x + 1	x – 3
#) 9b2x – 3b = 4x – 2;			д) x + --3---	= --1---	(9x + 1).
			a3	a2

2. При а их значениях a имеет бес онечное множество решений уравнение:

а) 6(ax – 1) + a = 3(a – x) – 5;

2	4	+ a(3 – x)?
б) --	(x – 1) = --
3	3

3. При а их значениях a не имеет решений уравнение: а) 2(3x – 2a) = 2 + ax;

б) a2x = a(1 + 5x) – 2 – 6x?

4. При а их значениях b уравнение: а) (a + 1)x = 2b – a;

б) (2a – 1)x = b + a – 1; в) (a + 2)x = 3b – a + 1

имеет решение для любо#о значения a? 5. Решить уравнение:

а)

--x-----–----a-

= 0;

б)

--x-----–----3-

+ -----

4-------

=

------------------2-----------------

;

x + 2

x + 2

a – 1

(a – 1)(x + 2)

в) x-- + x-------+----a-

+ --a

= 1;

#)

--x-----–----a-

= x-------+----a-

;

a

a + 3

3

a + 2

a + 1

д) --3-----x----–--------2 + x-------–----1-

+

2--

= 0;

е)

5-------+----x-------–--ax------

= 0.

a2 – 2a

a – 2

a

4 – x2

6.При а их значениях a аждый орень уравнения 2(x – 2a) =

=3 + a удовлетворяет условию x Ý [–1; 3]?

32

Ответы

1. а) Если a − 0, то x = a – 2 ; если a = 0, то нет орней; б) если a − 0,

------------

2

a − –5, то x =		4----------------a + 5 ; если a = 0, a = –5, то нет орней; в) если a − –2, a − 2,
		a
то x =	------------1 ; если a = –2, то x Ý R; если a = 2, то нет орней; ) если b − – 2-- ,
	a – 2			3
b − 2-- , то x = ---------------		1 -	; если b = 2-- , то x Ý R; если b = – 2-- , то нет орней; д) если
3	3b + 2		3	3
			1
a − 0, a − –3, a − 3, то x = a---------------------(a + 3)				; если a = 3, то x Ý R; если a = 0, a = –3,
			1	2
то нет орней. 2. а) При a = – -- ; б) при a = – -- . 3. а) При a = 6; б) при a = 3.
			2	3
		1	1
4. а) При b = – -- ; б) при b = -- ; в) при b = –1. 5. а) Если a − –2, то x = a; если
		2	2
				3( a – 3)
a = –2, то орней нет; б) если a − –3, a − 0,6, a − 1, то x = --------------------- ; если
				a + 3

a = –3, a = 0,6, a = 1, то орней нет; в) если a − –3, a − –1,5, a − 0, то x =

= – a(a2 + 3a – 9) ; если a = – 3, a = 1,5, a = 0, то орней нет; ) если a − –2,

-------------------------------------

3( 2a + 3)

a − –1, то x = –(2a2 + 3a); если a = –2, a = –1, то орней нет; д) если a − –3,

a − 0, a − 2, то x = ------------6 – a	; если a = –3, a = 0, a = 2, то орней нет; е) если
a + 3
a − –1,5, a − 1, a − 3,5, то x =		------------5	; если a = –1,5, a = 1, a = 3,5, то орней
		a –	1

нет. 6. a Ý [–1; 0,6].

33

Тема 4

1. Понятие ф н ции

2. Монотонность ф н ции

3. Четные и нечетные ф н ции 4. Линейная ф н ция и ее (рафи

5. Квадратичная ф н ция и ее (рафи

6. Ф н ция y = k и ее (рафи

--

x

СПРАВОЧНЫЙ МАТЕРИАЛ

1. Понятие ф н ции

1°. Зависимость одной переменной от дру#ой называют ф н - циональной зависимостью.

2°. Зависимость переменной y от переменной x называют ф н - цией, если аждому значению x соответствует единственное значение y. При этом используют запись y = f(x).

3°. Переменную x называют независимой переменной (или ар-ментом), а переменную y — зависимой переменной. Говорят, что y является фун цией от x.

4°. Значение y, соответствующее заданному значению x, называют значением ф н ции.

5°. Все значения, оторые принимает независимая переменная, образуют область определения ф н ции.

6°. Все значения, оторые принимает зависимая переменная, образуют множество значений ф н ции.

7°. Для фун ции f приняты обозначения: а) D(f) — область определения фун ции; б) E(f) — множество значений фун ции; в) f(x0) — значение фун ции в точ е x0.

2. Монотонность ф н ции

1°. Фун цию f(x) называют возрастающей на данном числовом промежут е X, если большему значению ар#умента x Ý X со-

34

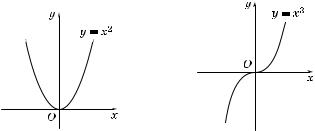
ответствует большее значение фун ции f(x), т. е. если для любых x1 и x2 из промежут а X та их, что x2 > x1, выполняется неравен-

ство f(x2) > f(x1).

2°. Фун цию f(x) называют бывающей на данном числовом промежут е X, если большему значению ар#умента x Ý X соответствует меньшее значение фун ции f(x), т. е. если для любых x1 и x2 из промежут а X та их, что x2 > x1, выполняется неравен-

ство f(x2) < f(x1).

3°. Фун цию, толь о возрастающую или толь о убывающую на данном числовом промежут е, называют монотонной на этом промежут е.

3. Четные и нечетные ф н ции

1°. Фун цию y = f(x) называют четной, если она обладает следующими двумя свойствами:

а) область определения фун ции симметрична относительно точ-и O (т. е. если точ а a принадлежит области определения, то точ-а (–a) та же принадлежит области определения);

б) для любо#о значения x, принадлежаще#о области определения фун ции, выполняется равенство f(x) = f(–x).

2°. Фун цию y = f(x) называют нечетной, если:

а) область определения фун ции симметрична относительно точ и O;

б) для любо#о значения x, принадлежаще#о области определения фун ции, выполняется равенство f(–x) = –f(x).

3°. Графи четной фун ции y = x2 изображен на рис. 1. 4°. Графи нечетной фун ции y = x3 изображен на рис. 2.

5°. Заметим, что не вся ая фун ция является четной или нечетной.

Рис. 1

Рис. 2

35

4. Линейная ф н ция и ее (рафи

1°.Фун цию, заданную формулой y = kx + b, #де k и b — не о- торые числа, называют линейной.

2°.Графи линейной фун ции y = kx + b есть прямая. 3°.Коэффициент k хара те-

ризует у#ол, оторый образует

прямая y = kx с положительным

направлением оси Ox, поэтому число k называют ловым о-

эффициентом. При этом:

а) если k > 0, то этот у#ол острый;

б) если k < 0, то этот у#ол тупой;

в) если k = 0, то прямая y = = kx совпадает с осью Ox.

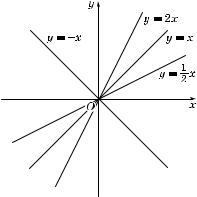
На рис. 3 изображены пря-

мые y = kx при k = – 1, k =	1	,
	--
Рис. 3	2

k = 1 и k = 2.

4°. Областью определения линейной фун ции служит множество R всех действительных чисел, та а выражение kx + b имеет смысл при любых значениях x.

5°. Уравнение вида kx + b = 0 называется линейным.

5. Квадратичная ф н ция и ее (рафи

1°. Фун цию, заданную формулой y = ax2 + bx + c, #де x, y — переменные, a, b и c — заданные числа, причем a − 0, называют

вадратичной.

2°. Областью определения вадратичной фун ции является множество R.

3°. Графи ом фун ции y = ax2 + bx + c является парабола. При этом:

а) если a > 0, то ее ветви направлены вверх; б) если a < 0, то ее ветви направлены вниз;

b

в) осью симметрии параболы служит прямая x = –------ .

2a

4°. Координаты вершины параболы находят по формулам

x		= –	b	, y		= y(x ) =	4ac – b2
	0		2----a--		0		---------------------- .
						0	4a

36

Рис. 4

На рис. 4 изображены #рафи и

1	x2, y = 2x2	1	x2,
фун ций y = --		и y = – --
2		3

а на рис. 5 — #рафи и фун ций y = = x2 + 4x + 3 и y = –2x2 + 7x – 5.

6. Ф н ция y = k и ее (рафи

--

x

1°. Если переменная y пропорциональна переменной x, то та ая зависимость выражается формулой y = kx, #де k − 0 — оэффициент пропорциональности.

2°. Если переменная y обратно пропорциональна переменной x,

k

то та ая зависимость выражается формулой y = -- , #де k − 0 — о- x

эффициент обратной пропорциональности.

3°. Область определения фун ции y = k есть множество чисел,

--

x

отличных от нуля, т. е. x Ý R, x − 0.

Рис. 5

37

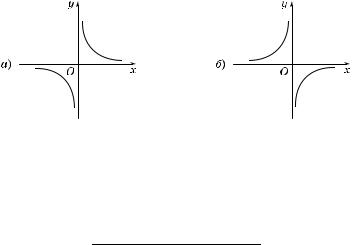
4°. Графи ом обратной пропорциональности y = k является ри-

--

x

вая, оторую называют иперболой. Она состоит из двух ветвей, симметричных относительно начала оординат. При этом:

а) если k > 0, то ветви #иперболы расположены в I и III оординатных четвертях (рис. 6, а);

б) если k < 0, то они расположены во II и IV оординатных четвертях (рис. 6, б).

Рис. 6

5°. Заметим, что #ипербола не имеет общих точе с осями оординат, а лишь с оль у#одно близ о ним приближается.

ЗАДАЧИ С РЕШЕНИЯМИ

1.При а ом значении параметра a прямая y = 2ax – 3 проходит через точ у A(1; –6)?

1.Подставив x = 1, y = –6 в уравнение прямой y = 2ax – 3, получим –6 = 2a – 3, от уда a = –1,5.

2.Ответ: a = –1,5.

2.При а ом значении параметра a параболы y = 3x2 + 2ax – 1 и

y= ax2 – 5x + 8 пересе аются в точ е с абсциссой x0 = 3?

1.Подставив значение x0 = 3 в уравнения парабол, получим равенство

3 · 9 + 6a – 1 = 9a – 15 + 8,

от уда находим a = 11.

2. Ответ: a = 11.

38

3. Найти все та ие a, что при любом b уравнение
ax + b = |x|	(1)

имеет решение.

1. Наиболее рациональный подход решению этой задачи — #еометричес ий.

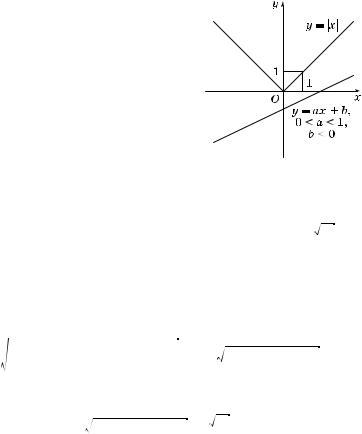
2. Рассмотрим #рафи и фун ций y = |x| и y = ax + b (рис. 7).

а) Если b < 0 и |a| m 1, то #рафи и не
пересе аются, а это значит, что урав-
нение (1) не имеет решений.
б) Если же b > 0 и |a| m 1, то хотя
#рафи и и пересе аются, это происхо-
дит не при любом значении b, а толь о
при b > 0.
в) На онец, если |a| > 1, то #рафи и
пересе аются при любом значении b.
3. Ответ: |a| > 1.	Рис. 7

4. При а их значениях параметра a расстояние между вершина-

ми парабол y = x2	2	и y = 3x2	19a2	29	?
	+ ax + --		+ 5ax + -------------	больше ----------
	3		12	3

1. Найдем оординаты вершин обеих парабол. Для первой из

	них x	= –	a	, y		= –	a2	+	2	, для второй x	= –	5a
			2--		1		--4---		3--			--6----
		1								2

a2

, y2 = –----- .

2

2. Расстояние между вершинами парабол выразится та :

d =		5a	a		2			a2	a2	2		2	1	9a4 + 64a2 + 64 .
		– ------	+ --			+		– -----	+ -----	– --			= ------
		6	2					2	4	3			12

3. Решив теперь неравенство

1	9a4 + 64a2 + 64	29
------		> ---------- ,
12		3

получаем a2 > 4.

4.Ответ: a Ý (–×; –2) Ÿ (2; +×).

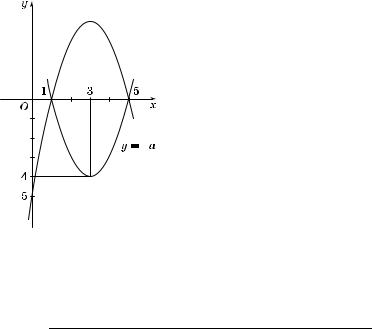
5.При а их значениях параметра a уравнение |x – 1|(x – 5) + a = 0 имеет ровно три решения? В ответе у азать наибольшее целое значение a.

39

				1.		Преобразуем заданное уравне-
					ние виду
						|x – 1|(x – 5) = –a.
				2.		Построим #рафи фун ции y =
					= |x – 1|(x – 5) (рис. 8). При x l 1 —
					эта часть параболы (x – 1)(x – 5) = x2 –
					– 6x + 5, а при x < 1 — часть параболы
					(1 – x)(x – 5) = –x2 + 6x – 5.
					3.	Графи фун ции y = –a есть пря-
					мая, параллельная оси Ox (рис. 8).
				4.		Из рисун а видно, что эта прямая
					пересе ает #рафи фун ции y = |x – 1| ç
					ç (x – 5) в трех точ ах, если –4 < a < 0.
				5.		Следовательно, a Ý (0; 4). Наи-
		Рис. 8			большее целое значение a из это#о ин-
					тервала равно 3.
				6.		Ответ: a = 3.

ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ

1. При а их значениях a является четной фун ция: а) y = (a – 3)x + 5a – 1;

б) y = –ax2 + (4a + 5)x + 3;

1

в) y = ----------------------------------------------------------------- ?

(a + 1)x2 – 2ax + 3a – 1

2. При а их значениях a является нечетной фун ция: а) y = (2a – 1)x – 6a + 5;

б) y =		x		;
	(----7---a------–---3----)------x---–----9-
в) y =	-------1-----	+	-----1-------	?
	x + a		x – a

3. Найти значения параметра a, при оторых заданная фун - ция монотонно возрастает и монотонно убывает:

а) y = (a – 1)x + a2 –3;

б) y = (2a + 5)x2 + 4x + a – 1;

в) y =

#) y =

7 – 3a

---------------- ; x

5

------------------------- .

(4a – 1)x

40