Задачи с параметрами и методы их решения

2.Нужно определить значения параметра a (a l 1), при аждом из оторых площадь заштрихованной фи#уры ABCD будет наибольшей.

3.Координаты точе A и D являются соответственно решениями систем уравнений

2			1	ax2,
	,		y = --
y = ax		и	2
y = 1			y = 1.

4. Координаты точе B и C являются соответственно решениями систем уравнений

2

1

ax2,

y = --

y = ax

,

и

2

y = 2

y = 2.

5. Учитывая, что абсциссы точе A, B, C, D по условию должны

быть неотрицательными, находим A

1

, D

2

; 1

, B

2

; 2

,

------- ; 1

--

--

a

a

a

C

2

.

------- ; 2

a

6. Точ и B и D имеют одина овые абсциссы, поэтому заштрихованная фи#ура состоит из двух частей:

а) фи#уры, лежащей под ривой y = ax2 и над прямой y = 1 на

промежут е от

1

до

2

;

-------

--

a

a

б) фи#уры, лежащей над ривой y =

1

и под прямой y = 2 на

-- ax2

2

промежут е от

2

до

2

--

------- .

a

a

7. Найдем площадь заштрихованной фи#уры:

2/a

2/

a

S =

∫

(ax2 – 1) dx +

∫

1

2

2 – --

ax2 dx =

1/

a

2/a

=

ax3

2/a

ax3

2/ a

1

10

– 2

2

.

--------- – x

+

2x – ---------

=

--

------

3

1/

a

6

2/a

a

3

361

1		10	– 2 2		в области a l 1 монотонно убывает.
8. Фун ция --		------
a		3

Поэтому ее наибольшее значение в этой области дости#ается при

10	2 .
a = 1 и равно ------ – 2
3
	10	2 .
9. Ответ: a = 1; S = ------ – 2
	3

4. Найти все значения параметра b (b > 0), для аждо#о из оторых площадь фи#уры, о#раниченной ривыми y = 1 – x2 и y = bx2, равна числу c. При а их c задача имеет решение?

1. Пусть b — не оторое фи сированное положительное значение параметра. Для это#о значения b найдем абсциссы точе пересечения #рафи ов фун ций y(x) = bx2 и y(x) = 1 – x2 (рис. 109). Они будут орнями уравнения bx2 = 1 – x2.

2. Решив это уравнение, получим

x1	= –-------1--------- , x2 = -----	--1--------- .
	b + 1	b + 1

3. Найдем площадь, о#раниченнуюривыми y = 1 – x2 и y = bx2:

	1/		b + 1
S =			∫	((1 – x2) – bx2) dx =
–1/			b + 1
=			b + 1		x	3		1/ b + 1
		x – ------------						=
				3				–1/ b + 1

Рис. 109	4
	= --
	3

	·	1	.	(1)
		b----+------1-

4. Та а выражение (1) по условию должно быть равно числу c,

то получаем соотношение		4	·	1	= c, от уда следует, что b =
		--		----------------
		3		b + 1
16	– 1.
= ---------
9c2

5. Задача имеет решение то#да и толь о то#да, о#да число c удовлетворяет системе неравенств

16	– 1 > 0,
---------
9c2	(2)

c > 0

362

(первое неравенство должно выполняться, та а по условию b > 0, а второе неравенство есть следствие то#о, что площадь фи#уры должна быть положительна).

5.	Решением системы (2) является интервал 0 < c <				4--	; ис омое
					3
значение b равно --		16-------	– 1.
	9c2
6.	Ответ: b =	--16-------	– 1; 0 < c <	4-- .
		9c2		3

5. Найти все значения параметра a (a > 0), при аждом из ото-

x2 + 2ax + 3a2

рых площадь фи#уры, о#раниченной параболой y = ---------------------------------------- и

1 + a4

a2 – ax

прямой y = ------------------- , является наибольшей.

1 + a4

1. Пусть a — фи сированное положительное число. Координаты точе пересечения параболы и прямой удовлетворяют системе уравнений

y =

x2

+ 2ax + 3a2

,

--

-----

----

--1-----+------a---4----

---------

y =

a2

– ax

.

--1-----

+------a---4---

2. Приравнивая правые части уравнений, приходим равенст-

ву x2 + 3ax + 2a2 = 0, от уда x

1

= –a, x

2

= –2a. То#да y

1

=

----2---a----2----

1 + a4

и y

=

3a2

. Ита , прямая пересе ает параболу в двух точ ах:

2

1-------+------a--4

B –a;

----2---a------2--

и C

–2a;

--

--3---a----2----

(рис. 110).

1 + a4

1 + a4

3. Вычислим площадь фи#уры CmBn.

Имеем

–a

a2 – ax

x2 + 2ax + 3a2

S(a) = ∫

–

dx =

--1-----+------a---

4---

----

---------1-----+-- a-------

4----

----

-----

–2a

1

–a

= –-----

--4 ∫ (x2 + 3ax + 2a2) dx =

1 + a

–2a

= –

1

x3

+

3ax2

+ 2a2x

–a

=

a3

.

----

-------

-----

-------2----

--

6----(---1------+-----a----4--)

1 + a4

3

–2a

Рис. 110

363

4.Нужно найти значение a, при отором фун ция S(a) принимает наибольшее значение на множестве a > 0.

5.Фун ция S(a) дифференцируема в аждой точ е, причем

S′(a) =	1	·	3a2(1 + a4) – 4a3·a3
	6--		-----	----	---------	--------------------	------------------ =
						(1 + a4)2
	=		1	·	a2(3 – a4)		.
			6--		--(---1----	--+----a---4----)--2--

Уравнение S′(a) = 0 имеет в области a > 0 единственный орень a = 43 .

6.В промежут е 0 < a < 43 производная S′(a) положительна,

ав промежут е 43 < a < +× она отрицательна. Следовательно, фун ция S(a) возрастает на промежут е 0 < a < 43 и убывает на промежут е 43 < a < +×.

7.Та а фун ция S(a) непрерывна в точ е a = 4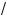3 , то в этой

точ е она принимает наибольшее значение, т. е. при a = 43 данная фи#ура имеет наибольшую площадь.

8.Ответ: a = 43 .

6.Найти все значения параметра a (a > 0), при аждом из оторых площадь фи#уры, о#раниченной параболой

	y = x2 – 2x 3			a	+ 3
			1-------	+----a---2-
и прямой y = –3x 3	a	+ 3 является наибольшей. Найти эту наи-
	1-------+----a---2-

большую площадь.

1. Пусть a > 0 — не оторое фи сированное число. Координаты точе пересечения у азанных линий удовлетворяют системе уравнений

	y = x2 – 2x 3			a	+ 3,	(1)
			1-------	+----a---2-
	y = –3x 3	a		+ 3.		(2)
		1-------+------a-2-

364

2. Приравнивая правые части этих уравнений, приходимвадратному уравнению

	x2 + x 3		a	= 0,
		1-------	+----a---2-

от уда следует, что парабола (1) и прямая (2) пересе аются в точ-

a

ах с абсциссами x1 = –3 --------------- и x2 = 0, причем x1 < x2.

1 + a2

3.Нетрудно установить, что фи#ура, площадь оторой требуется определить, находится ниже прямой (2) и выше параболы (1) на промежут е [x1; x2].

4.Вычислим ис омую площадь:

		0						a
		∫
S(a) =						–3x 3			+ 3 –				x2
								---------------
			a					1 + a2
	3	---------------
–		1	+ a	2
						x3	– 3	a	x2	0
			= –-----					---------------	· -----
					3			1 + a2	2				a
											3	---------------
										–		1	+ a	2

– 2x 3			a			dx =
		---------------		+ 3
		1	+ a2
		a
=	6----(---1------+-----a----2--) .

5.Чтобы найти значение a > 0, при отором фун ция S(a) принимает наибольшее значение, исследуем эту фун цию.

6.В аждой точ е области 0 < a < +× фун ция S(a) имеет производную

S′(a) =	1	+ a2 – a · 2a	=	1	– a2	.	(3)
	-------	6----(--1-----+----a----2---)--2------		(---1------	+-----a----2--)--2-
			6

7.Из выражения (3) следует, что на промежут е 0 < a < 1 производная S′(a) > 0, а на промежут е 1 < a < +× производная S′(a) < 0.

Значит, фун ция S(a) возрастает на промежут е 0 < a < 1 и убывает на промежут е 1 < a < +×.

8.Пос оль у фун ция S(a) непрерывна в точ е a = 1, ее наибольшее значение дости#ается при a = 1.

9.Ита , при a = 1 данная фи#ура имеет наибольшую площадь;

1

эта площадь есть S(1) = ------ .

12

1

10. Ответ: a = 1; S = ------ .

12

365

ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ

1. Найти все числа a, для аждо#о из оторых выполняется неравенство:

2

а) ∫ (a2 + (4 – 4a)x + 4x3) dx m 12;

1

a

б) ∫ (a – 4x) dx l 6 – 5a.

1

a

2. Найти все решения уравнения ∫ cos (x + 2a2 – a) dx = –sin 2a,

–a

принадлежащие отрез у [–1,5; –0,5].

2β

3. Найти все решения уравнения ∫ sin (x – β2) dx = sin 2β, при-

0

надлежащие отрез у [2; 3].

x

4. Найти ритичес ие точ и фун ции ∫ (sin2 2t – 2 cos2 2t + a)dt.

0

5. Найти все значения a, принадлежащие отрез у [0; 2π] и

a

удовлетворяющие уравнению ∫ sin x dx = sin 2a.

π/2

6.Найти значения параметра a, при оторых площадь фи#уры, о#раниченной линиями:

а) y = 3x3 + 2x, x = a, y = 0, равна 1;

		16	;
б) y = 8x2 – x5, x = 1, x = a, y = 0, равна ------
		3
4	9
в) y = ----- , x = 1, y = a, равна -- ;
x2	4
π	, равна	1
#) y = sin 6x, x = a, x = ------		-- .
18		6
7. Найти все значения параметра p (p > 0), при аждом из ото-
рых площадь фи#уры, о#раниченной параболой y = x2 + x3				p	+ 1
				---------------
				1 + p2

p

и прямой y = 2x3 --------------- + 1, является наибольшей.

1 + p2

366

8. Найти все значения параметра a (a > 0), при аждом из оторых площадь фи#уры, о#раниченной параболой y = –(1 + a2)2x2 + a и прямой y = 0, является наибольшей.

Ответы

1. а) 3; б) 2. 2. –	π	;	1 – 1 + 2π	. 3.	3π	. 4. Если a Ý [–1; 2], то x =	π n	ä
	--		------------------------------		------		------
	2		2		2		2

ä	1--	arccos 2----------------a – 1			; если a Ô [–1; 2], то ритичес их точе нет. 5.															--π	; 7------π ; 3------π ;
	4		3																	2	6	2
11	π	. 6. а) ä	2	; б) –1;		3	8	– 17	; в)	1	;	49	; ) –	π	;	π	. 7.	1. 8.	3 .
---------6	-		--							4--		------		------		--
			3									4		18		9

367

При л о же ни е 1

Те стовые задачи на составлениеравнений и неравенств с параметрами

ЗАДАЧИ С РЕШЕНИЯМИ

1. Две точ и начинают одновременно равномерное движение от вершины прямо#о у#ла вдоль е#о сторон. С а ой с оростью должна дви#аться первая из них, чтобы через t с после начала движения расстояние между ними было не менее 10 м, если известно, что с о- рость второй точ и на 2 м/с больше с орости первой?

1.Пусть x м/с — с орость движения первой точ и; то#да (x + 2) м/с — с орость движения второй точ и.

2.За t с точ и пройдут соответственно tx м и t(x + 2) м. При

этом расстояние между ними составит t2x2 + t2(x + 2)2 . 3. Задача сводится решению неравенства

t2x2 + t2(x + 2)2 l 10,оторое равносильно неравенству

	2t2x2 + 4t2x + 4t2 – 100 l 0.	(1)
4. Пусть D — дис риминант вадратно#о трехчлена
	f(x) = 2t2x2 + 4t2x + 4t2 – 100.	(2)
D	= 4t4 – 8t4 + 200t2 = –4t4 + 200t2	= 4t2(50 – t2).
Находим ----
4

По смыслу задачи t > 0 и x l 0.

5.Имеем D < 0 при 50 – t2 < 0, т. е. при t > 52 . То#да неравенство (1) справедливо при любом x l 0.

6.Имеем D = 0 при t = 52 . То#да неравенство (1) примет вид 100(x + 1)2 l 0 и, значит, оно та же справедливо при x l 0.

368

7. Рассмотрим теперь случай D > 0, т. е. 0 < t < 52 . То#давадратный трехчлен (2) имеет два действительных орня:

x1 =	– t – 50 – t2	– t + 50 – t2
	---------------------------------- ; x2 =	----------------------------------- .
	t	t

8. Очевидно, что x1 < 0 при любых значениях t. Поэтому остается решить систему неравенств

x l 0,

– t + 50 – t2	(3)
x l -----------------------------------	.
t

9. а) Мы установили, что орень x1 вадратно#о трехчлена (2) от-

рицателен. В силу теоремы Виета если при этом 4t2 – 100 m 0, т. е. 0 < t m 5, то орень x2 неотрицателен и решение системы (3) есть

x l	– t + 50 – t2
	----------------------------------- .
	t

б) Если же 4t2 – 100 > 0, т. е. 5 < t < 52 , то x2 < 0 и решением системы (3) служит любое x l 0.

10. Ответ: если t > 5, то x l 0;

если 0 < t m 5, то x l	– t + 50 – t2
	----------------------------------- .
	t

2. Из пун та A в пун т B, расстояние между оторыми равно s, вышли одновременно два пешехода; в тот же момент из пун та B

s

в пун т A выехал велосипедист. Проехав путь -- (от B A), велоси- k

2

педист встретил перво#о пешехода, а затем, проехав -- все#о пути,

3

он встретил второ#о пешехода. На а ом расстоянии l от них в момент встречи находился первый пешеход?

1.Пусть v — с орость перво#о пешехода, w — с орость велосипедиста.

2.То#да со#ласно условию задачи в момент их встречи выполняется равенство

s s – --

k s

----------- = ------- , v kw

от уда следует, что v = (k – 1)w.

369

3. Далее, время, оторое затратил велосипедист на прохождение пути от момента встречи с первым пешеходом до момента встречи со вторым пешеходом, определяется равенством

s	2	1		.
t = ---	--	– --
w	3	k

4.За это время t первый пешеход прошел от момента встречи

свелосипедистом путь

s(k – 1)(2k – 3) vt = ------------------------------------------ .

3k

5. Та им образом, расстояние l, на отором находился первый пешеход в момент встречи велосипедиста со вторым пешеходом, равно

s(k – 1)(2k – 3)	+	2	–	1	s =	s(2k – 3)	.
------------------3----k--------------------		3		--k		-----------3-------------

3

Заметим, что из условия задачи выте ает, что k l -- , причем

2

3

если k = -- , то пешеходы мо#ут идти с одина овыми с оростями.

2

2s

Кроме то#о, l m ------ , т. е. первый пешеход далее пун та B не движет-

3

ся. То#да, решив неравенство

s(2k – 3) 2s

------------------------ m ------ ,

3 3

5
находим, что k m -- .
2
6. Ответ: если	3	5	, то l =
	--	m k < --
	2	2

5	2s
если k l --	, то l = ------ .
2	3

s(2k – 3)

------------------------ ;

3

3. Расстояние между пун тами A и B равно s. Из пун та A в пун т B вылетел вертолет, а через время t в том же направлении вылетел самолет, оторый до#нал вертолет на расстоянии r от пун та A, затем долетел до пун та B и сразу повернул обратно. На расстоянии r от пун та B самолет встретил вертолет и вернулся в пун т A позднее, чем вертолет прибыл в пун т B. На с оль о раньше вертолет прибыл в пун т B, чем самолет вернулся в пун т A?

370