mat.analiz_1

2. існує границя

x→x

(

x

)

функції

y

= f

(

x

)

0

lim f

в точці x ;

0

3. грани ця функції дорівнює значенню функції в цій точ ці:

x→x

(

x

)

= f

(

0 )

.

lim f

x

0

Пр иклади неперервних функцій:

1. Степенева функція

y = xn ,

n N

неперервна в кожній точці x R .

0

Перевіримо всі три умови неперервності:

1. x0 D (xn )

= R; f ( x0 )= x0n .

2. lim xn = lim x x ... x = lim x lim x ... lim x = xn .

x→x0

x→x0

x→x0

x→x0

x→x0

0

n разів

(

)

(

x→x

x

=

f

0 )

.

3. lim f

x

0

2. Ціла раціональна функція (многочлен)

y = a

0

xn + a xn−1

+ a

xn−2 +... + a

n−1

x + a

n

1

2

неперервна в кожній то чці x0 R :

1. x0 R ;

f (x0 )= a0 x0n + a1 x0n−1 +... + an−1 x0 + an ;

2. lim

a

xn

+ a xn−1 + ... + a

n−1

x

+ a

n

)

= lim a

xn + lim a xn−1 +... + li m a

n

=

x→x (

0

1

x→x

0

x→x

1

x→x

0

0

0

0

= a0 x0n

+ a1 x0n−1 +... + an−1 x0

+ an

= f (x0 );

x→x

(

x

)

=

f

(

0 )

.

3. lim f

x

0

3. Дробово раціональна

функція

y =

a xn

+ a

1

xn−1

+... + a

н еперервна

0

n

b xm

+b

1

xm−1

+... +b

x R крім

0

m

тих,

які

перетво рюють

знаменник

в нуль.

Доводиться

аналогічно прикладу 2.

f (x)

Якщо функція

y

=

неперервна в точці

x0 , то роль границі

функції в точці x0

відіграє число

f (x0

. Тому, використавши означення

границі функції в точці, можна дати так е означення неперервн ої функції в точці.

Означення	13.2 (за Коші). Функція	y = f (x), визначена на
множині Х,	називається неперер вною	в точці , якщо

160

ε > 0 δ > 0, x X :

x − x0

< δ

f (x) − f (x0 )

< ε .

Як бачимо, в означенні неперервної функції замість проколеного

околу O* (x0 ),

як це було при

означенні границі функції,

тепер взято

просто окіл

O (x0 ), тому що в даном у разі функція

f (x)

в точці

x0

визначена, а нерівність

x − x0

< δ при x = x0

правильна.

Приклади неперервних функцій.

4.

Тригонометричні функції:

y = sin x ,

y = cos x

неперервні в кожній

точці

x0 R . Доведемо,

користуючись означенням 13.2,

що функція

y = sin x неперервна в точці x0 , тобто:

lim sin x = sin x0

ε > 0 δ > 0, x :

x − x0

<δ

sin x −sin x0

< ε

x→x0

Оцінимо модуль різниці значень функції в точках x і x0 :

sin x −sin x

=

2

sin

x − x

cos

x + x

≤ 2

sin

x − x

≤ 2

x − x0

=

x − x

< ε.

0

0

0

0

2

2

2

2

0

Отже,

якщо взяти δ =ε ,

то ми ε > 0 вказали δ =ε

таке,

що як тільки

x − x0

< ε , так і зразу буде виконуватись нерівність

sin x −sin x0

< ε , що

й

означає

неперервність

функції

y = sin x

в

точці

x0 .

Доведіть

самостійно неперервність функції y =

os x в точці x0 R .

Згідно з означенням границі функції в точці x0 в

термінах

послідовностей означення неперервної функції в точці

x0

можна

сформулювати так.

Означення

13.3

(за

Гейне). Функція

y = f (x),

визначена

на

множині

Х,

називається

неперервною

в

точці

,

якщо

для

довільної

послідовності

(xn ) O (x0 )∩ X

такої,

що

lim xn

= x0

{f (xn )}

n→∞

відповідна

послідовність

значень функції

збіжна

і

lim f (xn )= f (x0 ).

n→∞

161

(13.2)

Повернемося до формули (13.1):

lim f

(x )= f (x ) lim f (x) −lim f

(x )= 0

lim

f (x)− f (x

)

)

= 0.

x→x

0

x →x

x→x

0

x−x →0 (

0

0

0

0

0

Різниця x = x − x0 називається приростом аргумента, а різниця

f (x0 ) = f (x)−

f (x0 )

– приростом функції, який відповідає даному

приросту аргумента

x :

.

(13.3)

Тоді рівність (1 3.2) можна записати у вигляді:

.

(13.4)

Означення

13.4. Функція

y = f (x),

визначена

на множині

Х,

називається неперервною в точці

,

якщо границя прирос ту

фун кції дорівнює нулю при

x →0 .

Наведені тут чотири означення неперервної функції в точці є еквівалентні між собою в тому розумінні, що коли функція y = f (x) неперервна в точці за яким небудь одним означенням, то вона неперервна і за решто ю означень.

Пр иклади неперервних функцій:

5. Функція f (x)=

1

неперервна в кожній точці

x0

≠ 0 .

Використаємо

x

означе ння 13.4 і обчислимо приріст функції у точці x0

≠ 0 :

y = f (x0 +Δ x)− f ( x0 )=

1

−

1

=

x0 − x0 − x

= −

x

;

x0

+Δx

x0 (x0 + x)

x0 (x0 +

x)

x0

lim

y

= lim

x

= −

lim x

= −

0

= 0.

x→0

x0 (x0 +

x)

lim x0 (x0 +

x)

x02

x→0

x→0

x

→0

Отже, f (x)=

1

неперервна в точці x0

≠ 0 .

x

162

u =ϕ (x)

Неперервність суми, добутку, частки.

Теорема 13.1. Якщо функції f (x) і ϕ (x) є неперервними в точці

x0 , то в цій точці будуть неперервними і функції f (x)±ϕ (x),

f (x) ϕ(x).

Теорема 13.2. Якщо функції f (x) і ϕ (x) є неперервними в точці x0

і ϕ(x0 )≠ 0 , то в точці x0 неперервною є функція ϕf ((xx)).

Доведення.

Застосуємо означення 13.1 неперервної функції в точці. Позначимо

F (x)= ϕf ((xx)) і перевіримо для цієї функції три умови неперервності.

1.

F (x0 )

=

f (x0 )

.

ϕ(x0 )

2. Існує lim F (x)= lim

f (x)

=

ϕ(x)

x→x0

x→x0

3.

lim F

(

x

)

= F

(

x

.

x→x

0 )

0

	lim f	(x)				f (x0 )			= F (x0 ).
	x→x0				=
	x→x	(	x	)		ϕ	(	0 )
	limϕ							x
	0

Аналогічно доводиться теорема 13.1.

Приклад 6. Функції y =tgx і y = ctgx є неперервними в кожній точці області визначення як частка неперервних функцій sin x і cos x .

Неперервність складеної функції.

Теорема 13.3. (неперервність складеної функції). Якщо функція f (u) неперервна в точці u0 (α; β ), функція

163

неперервна в точці x0 (a; b), причому u0 =ϕ(x0 ), то складена функція f (ϕ(x)) неперервна в точці x0 .

Доведення.

u→u

(

)

(

0 )

1

0

lim f

u

= f

u

ε >

0 δ >0,

u :

u −u

0

Оскільки

(

0 )

(

1 )

x→x

(

x

)

=ϕ

1

>0

а значить i

1

limϕ

x

ε

ε

=δ

0

ϕ(x)−ϕ(x0 )

< δ1

u −u0

< δ1 ,

тому

перетворень

<δ1 f (u)− f (u0 ) <ε;

δ >0, x: x −x0 <δ

отримали ланцюжок

x − x0 <δ ϕ(x)−ϕ(x0 ) <δ1 u −u0 <δ1 f (u)− f (u0 ) <ε

f (ϕ(x))− f (ϕ(x0 )) <ε.

Звідки, на основі теореми про границю композиції функцій, випливає, що

lim f (ϕ(x))= f (ϕ(x0 )).

x→x0

Це означає, що f (ϕ(x)) неперервна в точці x0 , що й треба було довести.

Перехід до границі під знаком неперервної функції.

Висновок з теореми 13.3. Операція граничного переходу комутативна з операцією взяття неперервної функції:

																	.		(13.5)
Доведення.
Оскільки функції				f (ϕ(x)) і ϕ (x) неперервні в точці x0 , то
x→x			(	ϕ	(	x	))		=	f	(	ϕ	(	0 ))			,
lim f														x				( ( ))	(x→x0	( ))
	0																x→x0
f	(x→x0			ϕ(x)				)		f	(			0	)	)	lim f	ϕ x	= f limϕ x .
		lim							=			ϕ(x					,

164

Здоведеної теореми випливає, що якщо функція f (u) неперервна

вінтервалі (α; β ), а u =ϕ(x) – неперервна функція в інтервалі (a;b),

причому x (a; b) відповідна точка ϕ(x)= u (α; β ), то складена функція f (ϕ(x)) неперервна в інтервалі (a; b).

Приклад 7. Функція

f (u )= tgu

неперервна в інтервалі

−π ;

π

,

2

2

функція u = sin x неперервна на всій числовій прямій (−∞;∞), причому

x (−∞; + ∞)

u = sin x [−1; 1]

π

;

π

Тому

складена

−

2

2

.

функція y = tg sin x неперервна на проміжку (−∞;

+ ∞).

Одностороння неперервність.

Означення13.5. Функція y = f (x)

називається

неперервною

в

точці

0

справа,

якщо

x→x +0

f

(

x

)

=

f

(

0 )

;

і

називається

x

lim

x

0

0

x→x −0

(

)

( 0 )

x

=

f

.

неперервною зліва в точці x , якщо

lim f

x

0

Отже,

згідно з

означенням,

функція

y = f (x)

в

точці

x0

буде

неперервною справа (зліва) тоді і тільки тоді, коли виконуються умови:

1. Функція y = f (x) повинна бути визначена на піввідрізку

[x0 , x0 +δ )((x0 −δ; x0 ]) , де δ > 0.

2.В точці x0 функція f (x) повинна мати праву (ліву) границю.

3.Ця права (ліва) границя повинна дорівнювати значенню функції f (x) в точці x0 .

165

	arctg			1	,	x ≠ 0,
				x
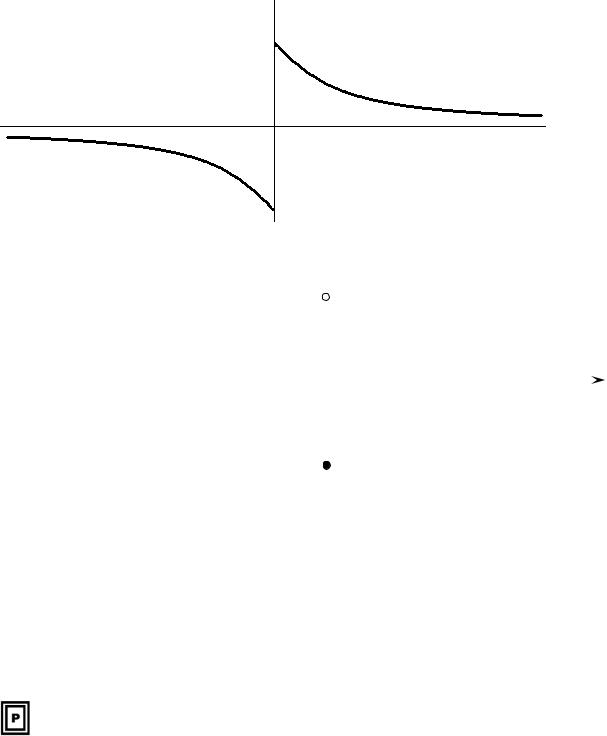
	Приклад 8. Дослідити функцію y =	π
			,			x = 0,
	−	2

на неперервність в точці x0 = 0 зліва.

Розв’язання.

Якщо x →0 −0, то

1

→ −∞, то

arctg

1

→ −

π

, то

x

x

2

1

π

lim arctg

= −

(рис. 13.1).

2

x→0−0

x

y

π

2

x

−π2

			Рис. 13.1
	Якщо x →0 +0, то	1	→ +∞, то arctg	1	→ +	π	, то	lim arctg	1	=	π .
		x		x		2			x
								x→0+0			2

lim y(x)= y(0), отже функція y (x) неперервна в точці x0 = 0 зліва.

x→0−0

На мові „ε −δ ” означення неперервної функції в точці буде формулюватися таким чином.

	Означення		13.6. Функція			y = f (x),	визначена на	піввідрізку
	[x0 ; x0 +δ )		((x0	−δ;	x0 ])	називається неперервною в точці x0
справа (зліва),				якщо	ε > 0 δ > 0		таке, що з нерівності
	0 ≤ x − x0 <δ			(−δ < x − x0 ≤ 0)			випливає	нерівність
	f (x)− f (x0 )		< ε .

З теореми про границю суми, добутку, частки двох функцій й означення границі функції в точці x0 справа (зліва) випливає, що

166

сума, різниця, добуток і частка (якщо знаменник не дорівнює 0 в точці x0 ) є функції, неперервні в точці x0 справа (зліва).

З означення неперервної функції в точці x0 справа і зліва і теореми

про односторонні границі функції в точці випливає:

Теорема 13.4. Для того, щоб функція

f (x)

була неперервною в

точці x0 , необхідно

і достатньо, щоб функція

f (x)

була

неперервною в точці x0 і справа, і зліва.

Доведення.

Необхідність.

Нехай f (x)

– неперервна в точці x0 , тобто

(

)

(

0 )

x→x

(

)

(

0 )

0

lim f

x

= f

x

ε >0 δ >0, x X :

x −x

<δ

f

x

− f

x

<ε,

0

тому

0 ≤ x − x0

<δ

f (x)− f (x0 )

<ε f (x) – неперервна справа в точці x0 ,

−δ < x −x0 ≤0

f (x)− f (x0 )

<ε f (x) – неперервна зліва в точці x0 .

Достатність.

Нехай f (x)

– неперервна в точці x0 зліва і справа, тобто

ε > 0

δ1 > 0,

x X :

−δ < x − x0 ≤ 0

f (x)− f (x0 )

< ε ,

(13.6)

ε > 0 δ2

> 0, x X :

0 ≤ x − x0 <δ2

f (x)− f (x0 )

< ε .

(13.7)

Виберемо δ = min{δ1 ; δ2 },	тоді нерівності (13.6) і (13.7) виконуються
одночасно.
Отже, δ > 0, x X :	−δ < x − x0 < δ		f (x)− f (x0 )		< ε , а це
й означає, що функція f (x)	неперервна в точці x0 .

167

План:

1.Точки розриву та їх класифікація.

2.Границя і точки розриву монотонної функції.

3.Показниковa функція та її основні властивості.

Точки розриву та їх класифік ація.

Означення 14.1. Якщо функція y = f (x) в точці x0 не є неперервною, то точка x0 називається точко ю розриву функції , а са ма функція при ц ьому називається розривною в точці .

Отже, згі дно з означенн ям функція y = f (x)	в точці x0 буде
розривною, а точка x0 точкою розриву функції f (x),	якщо в цій точці

порушується принаймні одна з трьох умов неперервності:

1)функція y = f (x) не визначена в т очці x0 , однак в усіх інш их точках деякого око лу точки x0 вона визначена;

2)в точці x0 не існує границі ф ункції f (x) або lim f (x)= ∞;→

x x0

3)границя функції f ( x) в точці x0 , якщо існує, не дорівнює значенн ю цієї ф ункції в точці x0 .

168

Означення

14.2.

Якщо

не

виконується

співвідношення

lim

f (x) = f (x )

lim f

(x)= f (x )

)

, то кажуть, що функція

x→x0 +0

0

(x→x0 −0

0

f (x) має розрив в

точці x0

справа (зліва).

Приклад 1. Дослідити на неперервність функцію (рис 14.1):

1

,

−1 < x < 0,

x

0 ≤ x <1,

x,

f (x)= 3, x =1,

−x2 + 2x, 1 < x ≤ 2,

2 < x ≤ 3.

2,

Розв’язання.

В точці x = −1 функція

f (x) розривна справа,

оскільки значення

функції f (−1) не визначене. В точці x = 0 функція f (x)

розривна зліва,

оскільки

lim f (x)= lim

1

= −∞

і

неперервна

справа,

оскільки

x

x→0−0

x→0−0

lim x = f

(0)= 0 .

x→0+0

В точці x =1

функція

f (x) розривна справа

і

зліва,

оскільки

lim x =1 ≠ f (1)= 3;

lim

(

−x2

+ 2x

)

=1 ≠ f (1)= 3.

x→1−0

x→1+0

В точці x = 2 функція f

(x)

неперервна

Y

зліва, оскільки lim

(

−x2

+ 2x

)

= 0 = f (2)= 0 ,

3

x→2−0

(2)= 0 .

розривна справа, бо lim 2 = 2 ≠ f

2

x→2+0

В точці x =3 функція

f (x)

неперервна

1

X

зліва, бо lim 2 = 2 = f (3)= 2.

-1

0

1

2 3

x→3−0

В залежності від того, яка з трьох умов

-1

неперервності функції в точці не

-2

-3

Рис. 14.1

169