mat.analiz_1

f (x) < H :

sin πx = 0;

ні до другого

Приклад 5: y = −sin2 πx : D(y): −sin2 πx ≥ 0 ;

πx =πn, n Z; x = n, n Z .

D(y)= Ζ, тому така функція не належить ні до першого, класу функцій.

Монотонні, обмежені, парні, непарні, періодичні функції.

Розглянемо інший спосіб класифікації функцій, в основі якого лежать властивості дійсних чисел.

Оскільки множина значень функції y = f (x) є числовою множиною, то вона може бути обмеженою зверху, обмеженою знизу, обмеженою і необмеженою. Тому виділимо аналогічні класи функцій.

Обмежені функції.

Означення 6.1. Функції y = f (x), визначена на множині X називається обмеженою зверху на цій множині, якщо існує таке число M , що x X правильна нерівність f (x)≤ M :

df

(y = f (x) −обмежена зверху на X ) ( M , x X : f (x) ≤ M ) . (6.2)

Означення 6.2. Функції y = f (x), визначена на множині X називається обмеженою знизу на цій множині, якщо існує таке число К, таке що x X правильна нерівність f (x)≥ K :

	df	.	(6.3)
	(y = f (x) −обмежена знизу на X ) ( K, x X : f (x) ≥ K )
	Означення 6.3. Функціяy = f (x), обмежена на	множині X

зверху і знизу називається обмеженою на цій множині.

Означення 6.4 рівносильне такому:

Означення 6.4. Функція y = f (x), яка визначена на множині X, називається обмеженою на цій множині, якщо існує число H > 0 таке, що x X правильна нерівність

df	(6.4)
( f (x) − обмежена на X ) ( H > 0, x X : f (x) < H ).

70

Монотонні функції.

Множина R і будь яка її підмножина впорядкована, тобто якими б не були два дійсних числа a і b, ми можемо сказати, що або a < b , або a > b , або a = b . Якщо тепер ми маємо функцію y = f (x) і два значення аргументу x1, x2 , то або f (x1 )< f (x2 ), або f (x1 )> f (x2 ), або f (x1 )= f (x2 ). Цікавими є класи функцій, які або зберігають відношення, яким воно було між значеннями аргументів, або

змінюють його на протилежні.		y = f (x)
Означення 6.5. Функція			визначена на множинні X ,
називається	зростаючою		(спадною,	неспадною,
незростаючою), якщо для будь яких точок				x1 , x2 X : x1 < x2
правильна		відповідна		нерівність:

f (x1 )< f (x2 )(f (x1 )> f (x2 ), f (x1 )≤ f (x2 ), f (x1 )≥ f (x2 ))

Зростаючі, незростаючі, спадні й неспадні функції на множині E називаються монотонними на цій множині, а зростаючі і спадні функції називаються строго монотонними.

y =

зростаюча на X f (x)− спадна на X

незростаюча на X

неспадна на X

		x , x
	df	1 2

X , x1 < x2 : f (x1 ) < f (x1 ) > f (x1 ) ≥ f (x1 ) ≤

f (x2 ) f (x )

f (x2 ) (6.5)

f (x22 )

Приклад 6. Дослідити на монотонність лінійну функцію y = kx +b, x R.

Розв’язання.

Візьмемо довільні значення x1, x2 R : x1 < x2 . Отже, різниця x1 − x2 < 0, і оцінимо різницю значень функцій в цих точках:

y(x1) − y(x2 ) =(kx1 +b)−(kx2 +b) = kx1 +b −kx2 −b = k (x1 − x2 ).

Якщо:

а) k > 0 , y(x1 )− y(x2 )<0 , y(x1 ) < y(x2 ), тобто функція зростає на

R ;

71

б)	k < 0 , y(x1 )− y(x2 ) >0 , y(x1 ) > y(x2 ), тобто функція спадає на
R ;	k = 0 , y(x1 )− y(x2 )=0 , y(x1 ) = y(x2 ), тобто функція стала на
в)
	R .	y = f (x) називається	кусково
	Означення 6.6. Функція
	монотонною на проміжку	X , якщо його можна розбити на
такі проміжки X1, X2 ,... , на кожному з яких функція			f (x) буде
монотонна.
	Парні, непарні функції.

Множина R симетрична відносно початку координат. Якщо область визначення функції y = f (x) – симетрична відносно 0, то цікаво виділити функції, графіки яких теж мають певну симетрію. З геометричної точки зору симетрія може бути осьовою (відносно

прямої) і центральною (відносно точки).

Означення 6.7. Функція y = f (x) називається парною, якщо

	1) ( x R) (x D(f ) − x D(f )),	(6.6)
	2) ( x D(f ))(f (− x)= f (x)).

Означення 6.8. Функція y = f (x) називається непарною, якщо

1)	( x R) (x D(f )) − x D(f ),	(6.7)
2) ( x D(f ))( f (− x)= − f (x)) .

Функції, які не є парними або непарними, називають ні парними,

ні непарними.
Графік		парної	функції	симетричний
відносно	осі	Oy .	Справді,	нехай	точка
A(x; f (x))	належить графіку парної функції,
тоді точка B(−x; f (−x)) або B(−x; f (x))					також

належить графіку функції. А ці точки

симетричні відносно осі ординат (рис. 6.2).

Рис.6.2

72

Розв’язання. Нехай Т – період функції, отже:

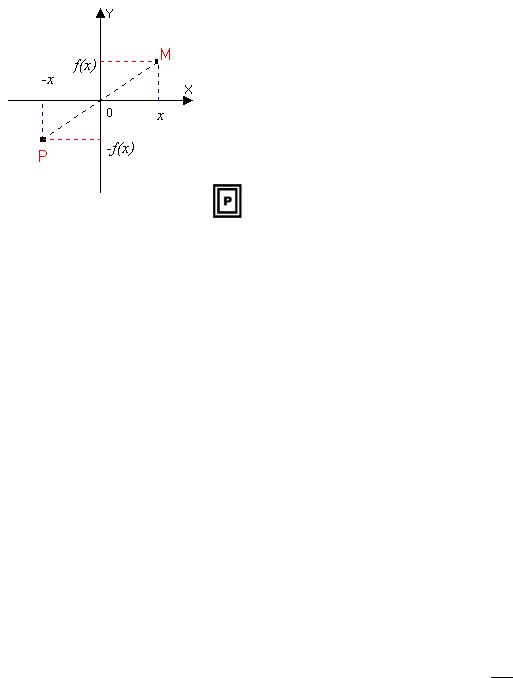
	Графік непарної		функції		симетричний
	відносно точки	0.	Справді,		нехай точка
	M (x; f (x)) належить графіку непарної функції,
	тоді точка P(−x; f (−x))			або	P(− x; − f (x))
	також належить графіку функції. А ці точки
	симетричні відносно початку відліку (рис.6.3).
	Періодичні функції.					y = f (x)
Рис.6.3	Означення	6.9.		Функція
	називається періодичною на множинні

Х , якщо існує таке число T ≠ 0 , що для всіх x X :
	1) x +T, x −T X ,		(6.8)
	2) f (x +T ) = f (x −T ) = f (x).

Приклад 7. Дослідити на періодичність y = sin (kx +b).

y(x +T ) = y(x),

sin (k (x +T )+b)= sin (kx +b),

sin (k (x +T )+b)−sin (kx +b)= 0 ,

2sin

k (x +T )+b − kx −b

cos

k (x +T )+b + kx +b

= 0,

2

2

)= 0 ,

kT

kT

kT

kT

sin 2

cos(kx +b + 2 )= 0 ,

sin 2 = 0 або cos(kx +ϕ +

2

Оскільки

cos(kx +ϕ + kT2 )

не

дорівнює нулю

тотожно,

то y (x)

періодична, якщо sin kT = 0

,

kT =πn,n Z ,

T =

2πn

, n

Z .

2

2

k

Найменший додатний період отримаємо при n =1, T = 2kπ

73

Базисні функції та основний метод побудови функцій. Клас елементарних функцій.

Розглянемо ще один принцип класифікації. За базисні візьмемо такі функції:

1)	f (x) = C;	2) f (x) = x;
3)	f (x) = ax (a > 0, a ≠1);	4)	f (x)= loga x (a > 0, a ≠1);
5)	f (x) = xa , деα R;	6)	f (x) = sin x;
7)	f (x)= cos x;	8) f (x)= arcsin x;
9)	f (x) = arccos x;	10)	f (x) = arctgx.

Означення 6.10. Базисні функції і функції, які можна одержати з базисних виконанням скінченного числа арифметичних операцій і композицій називають елементарними функціями. Зокрема функції, які можна одержати з сталих і степеневої функції за допомогою скінченного числа операцій додавання, віднімання, множення і композицій (+;–; ; ) називаються цілими раціональними функціями або многочленами:

P(x)= a0 xn +a1xn−1 +... +an−1x +an ,деai R, i = 0,n, n N {0} (6.9)

Якщо крім вказаних операцій приймає участь ще ділення, то функції називаються дробово раціональними функціями:

	P(x)		a xn +a xn−1		+... +a
y =						, де ai ,bj R, i = 0,n; j = 0,m; n,m N {0}					.
		0		1	n
		=
	Q(x)		b xm +b xm−1		+... +b
		0		1	m

Означення 6.11. Ірраціональними називаються елементарні функції, які не є раціональними і можуть бути задані за допомогою композиції скінченного числа раціональних функцій, степеневих функцій з раціональними показниками і арифметичних операцій.

Означення 6.12. Елементарні функції, які не є раціональними або ірраціональними, називаються трансцендентними.

74

Рис. 6.6. Парні функції

Функції

парні		непарні		ні парні ні непарні

( y =

( y =

f (x)	– парна на D ( f ))	df 1. x R : x D( f ) − x D( f ),
			2.	x D( f ): f (−x)= f (x),

f (x)	df	1. x R : x D( f ) − x D( f ),
	– непарна на D ( f ))		2	x D( f ): f (−x)= − f (x)

Приклади:

1)

2)

y

N 0 M x y = cos x – парна на R .

y

N

		y =tgx – непарна на
O	x	R \ {π2 +πn, n Z}.

M

y

y = ax2 +bx +c,b ≠ 0,c ≠ 0 – не

3)

парна

O

x

4)

y
O	1	x

y = loga x, a > 0, a ≠1 – не парна і не не парна

(0;+∞)

75

Приклади:

5)f (x)=log2 cos x – парна оскільки f (−x)=log2 cos(−x)=log2 cos x = f (x).

6)f (x)= sin (sin (sin x)) – не парна f (−x)= sin (sin (sin (−x)))=

=sin (sin (−sin x))= sin (−sin (sin x))= −sin (sin (sin x))= − f (x).

7)f (x)= x5 + 3x3 −1 – ні парна, ні непарна f (−x)= (−x)5 + 3(−x)3 −1 =

Рис. 6.7. Періодичні функції

Функції

							неперіодичні
		періодичні
			df		T > 0,		x, x +T, x −T X :
		(y = f (x), x X −періодична на X )
				f (x −T ) = f (x) = f (x +T )
Приклади:

y

1)

x

2)

y

π π

2

3) y

1

4)

-2

-1

0

1

2

x

y

x

f (x)=ctg x – періодична з періодом T =π .

f (x)=sin x – періодична з періодом T = 2π .

x

f (x)={x}:= x −[x] – періодична з періодом T =1.

		cos x			1, cos x > 0,
f (x)=					={−1, cos x < 0,	– періодична з періодом
		cos x

T = 2π .

76

Рис. 6.4. Обмежені і			Функції
необмежені функції
обмежені			обмежені		необмежені			необмежені
					зверху
			знизу
		обмежені				необмежені
			df
(y = f (x) −обмежена зверху на X ) ( M , x X : f (x) ≤ M )
			df
(y = f (x) −обмежена знизу на X ) ( N, x X : f (x) ≥ N )
			df	X : f (x) < H )
( f (x) − обмежена на X ) ( H > 0, x
			df
( f (x) − необмежена зверху на X ) ( M , x0 X : f (x0 ) > M )
			df	x X : f (x ) < K )
( f (x) − необмежена знизу на X ) ( K
Приклади:
		y	y =		1	обмежена зверху на R,
1)					x2 +1
		O	x				1	≤1 (M =1).
			оскільки x R :
y							x2 +1
		y =	1 обмежена знизу на інтервалі (0;1), оскільки
2)
			x3
		x (0;1) : 1 >1 (K =1).
			x3
O	1		y = cos x обмежена на R, оскільки
3)		y
			x R : cos x ≤1			(H =1)
		O
			1,		x > 0,
					x = 0, обмежена на R , оскільки
4)		y	y = signx = 0,
			−1,		x < 0,
		1
			x R : signx ≤1 (H=1).
	−1	1	x
		−1	y =log2 x необмежена на R+ .
5)
y
			77
O	1	x

Рис. 6.5. Монотонні і

Функції

немонотонні функції

монотонні

немонотонн

зростаюча на X

x1, x2 X , x1 < x2

: f (x1 ) < f (x2 )

спадна на X

df

f (x ) > f (x )

y = f (x)−

незростаюча на X

f (x1 ) ≥ f (x2 )

неспадна на X

f (x1 ) ≤

f (x2 )

1

2

Зростаючі, незростаючі, спадні й

неспадні

функції

на

множині X

називаються

монотонними функціями.

Функція

y = f (x) називається кусково монотонною на

проміжку

X , якщо його можна

розбити на такі проміжки X1, X2 ,... , на кожному з яких функція f (x) монотонна.

Приклади:

y

(12)x

1)

y =

– спадна на R,

1

O

x

3)

y

y =

x −1

y =[x] –

y

–

2

неспадна на R,

1

2)

зростаюча на

−3 −2

−1

3 x

[1;+∞] ,

O

1

2

−1

O

1

−2

−3

5)

1

y = x3 –

y =

– спадна на

зростаючана R

4)

y

x3

y

множині

D ( f )= (−∞;0) (0; +∞),

O

O

6)

y = cos x не монотонна на R .

78

Класифікація функцій

(Рис.6.1) І. За структурою області визначення.

Функції

Функції натурального аргументу (числові
		Функції неперервного аргументу
послідовності) y = f (n),n N		y = f (x), D(f ) – проміжок або сукупність
		проміжків

(Рис.6.2) ІІ. За властивостями дійсних чисел.

			Функції
обмежені		монотонні		парні,
необмежені		немонотонні		не парні,

Інші функції

періодичні

неперіодичні

79