mat.analiz_1

Приклади.

1

1

1

1.

f (x)=

, x (0;1). Візьмемо x′ = xn′ =

; x′′ = xn′′ =

:

x

2n

n

xn′ − xn′′

=

1

−

1

=

1

<δ

(ε ), однак

f (xn′)− f (xn′′)

= n ≥1 >ε .

2n

n

2n

1

Отже,

якщо взяти ε0 0;

, то для нього не існує відповідного

2

δ (ε )> 0 такого, щоб

f (xn′)− f (xn′′)

≤ε0 . А це й означає, що неперервна

в

кожній точці інтервалу (0;1)

функція

f (x)=

1

не

є рівномірно

x

неперервна на (0;1).

2.

f (x)= x2

неперервна на R , але не є рівномірно неперервною на R .

Дійсно, візьмемо xn′ =

n +1; xn′′ =

n, n N, f (xn′)= n +1;

f (xn′′)= n .

lim

xn′ − xn′′

= lim( n +1

−

n )= lim

1

= 0, однак

n +1 + n

n→∞

n→∞

n→∞

f (x′ )− f (x′′)

=

n +1−n

=

1 >ε

0

(0; 1).

n

n

Зауважимо, що якби ми розглядали квадратичну функцію на відрізку, а не на всій числовій прямій, то неперервність функції забезпечила б рівномірну неперервність. Це гарантує фундаментальна теорема Кантора.

Теорема 16.1 (теорема Кантора). Якщо функція f (x) визначена і неперервна на відрізку [a;b], то вона і рівномірно неперервна на цьому відрізку.

Доведення проведемо методом від супротивного.

( f (x)− не є рiвномiрно неперервна на X )

( ε0 > 0, δ > 0 x′, x′′ X : x′− x′′ <δ , однак f (x′)− f (x′′) ≥ε0 ).

190

Якщо

остання

нерівність

виконується

δ > 0,

то

виберемо

δ =1;

1

; ... ;

1

; .... Тоді для:

2

n

δ =1

x1′, x1′′ [a;b]:

x1′ − x1′′

<1, однак

f (x1′)− f (x1′′)

≥ε0 ;

δ =

1

x2′, x2′′ [a;b]:

x2′ − x2′′

<

1

, однак

f

(x2′)− f (x2′′)

≥ε0 ;

2

2

...................................................................................................

δ =

1

xn′, xn′′ [a;b]:

xn′

− xn′′

<

1

, однак

f (xn′)− f (xn′′)

≥ε0 ; (16.1)

n

n

....................................................................................................

Отримали дві послідовності (xn′) і (xn′′) з відрізка

[a;b], вони є

обмеженими

і

за теоремою Больцано Вейєрштрасса, наприклад, з

послідовності

(xn′) можна виділити

збіжну підпослідовність (xn′k ):

lim xn′ = x0 ,

x0 [a;b].

k→∞

k

Для підпослідовності (xn′k ) побудуємо підпослідовність (xn′′k ) (xn′′)

, яка також буде збіжна до x0 :

xn′′k − x0

=

(xn′′k

− xn′k )+(xn′k

− x0 )

≤

xn′′k − xn′k

+

xn′k − x0

<

1

+

xn′k − x0

<δ .

nk

Оскільки f (x)

неперервна в точці x0 [a; b], то за означенням за Гейне

маємо:

lim x'

= x ,

lim

f

(

x'

)

=

f (x

),

→∞

nk

0

→∞

nk

0

lim (f (xn' k )− f (xn''k ))= 0 .

k

= x ,

k

f

(

x''

)

=

f (x

lim x''

lim

),

k→∞

k

→∞

nk

0

k→∞

nk

0

Отже,

ε > 0, в тому числі і ε0 , маємо:

f (xn′k )− f (xn′′k )

< ε , але за

побудовою (16.1) послідовностей (xn′)і (xn′′)

:

f (xn′k )− f (xn′′k

)

≥ ε0 .

191

Останні дві нерівності є несумісними. Таким чином, припущення про те, що існують відрізки і неперервні на них функції, які не будуть рівномірно неперервними, неправильне.

Неперервність оберненої функції.

Розглянемо теореми, які дають достатні умови існування та неперервності оберненої функції.

Теорема 16.2. Якщо функція y = f (x) визначена на відрізку [a;b], неперервна і зростаюча (спадна) на цьому відрізку, то для цієї функції на відрізку f (a); f (b) ( f (b); f (a) ) існує обернена функція x = f −1 (y), яка на відрізку f (a); f (b) ( f (b); f (a) ) є

також неперервною і зростаючою (спадною).

Доведення.

y	f (x)	І. Розглянемо випадок, коли						y = f (x)
B
		на	відрізку			[a;b]	визначена,
		неперервна			і	зростає.		Нехай
c2 = c +δ2		f (a) = A;		f (b) = B . Тоді за другою
C		теоремою Больцано – Коші (про
c1 = c −δ1		проміжне значення) для будь якого
A		числа	C	(A < C < B) на			[a;b] існує
a	c −ε c c +ε b x	принаймні			одна	точка	c	така, що
		f (c) = C . Оскільки f (x)					– зростаюча,
	Рис. 16.2	то не існує іншої точки c′ ≠ c , в якій би

f (c′) = C . Отже, кожному C [A; B] відповідає одна точка c [a;b], а це й означає, що на відрізку [A; B] існує обернена функція x = f −1 (y).

192

ІІ. Доведемо, що функція x = f −1 (y) є неперервною в точці C [A; B]. Використаємо означення неперервності за Коші. Візьмемо досить мале

додатне число ε таке,

щоб точки c −ε

і c +ε належали відрізку [a;b].

Нехай f (c −ε )= C1 , f (c +ε )= C2 . Позначимо

C −C1 =δ1 , C2 −C =δ2 C1 = C −δ1 , C2 = C +δ2 , δ1 > 0, δ2 > 0 і

виберемо

δ = min{δ1 ,δ2 }.

Тоді

y [A; B]:

y −C

<δ

x −c

< ε .

Отже, функція x = f −1 (y) є неперервною у точці

C [A; B]. Оскільки C

є довільною точкою відрізка [A; B], то

f −1 (y) є неперервною на всьому

відрізку.

ІІІ. Доведемо тепер,

що

f −1 (y)

на

відрізку [A; B] є зростаючою.

Методом від супротивного. Нехай

y1 , y2 [A; B]: y1 < y2 f −1 (y1 )≥ f −1 (y2 )

x1 ≥ x2 .

Але, оскільки функція y = f (x) є зростаючою, то

x1 ≥ x2 f (x1 )≥ f (x2 )

y1 ≥ y2 .

Отже,

y1

< y2

і y1

≥ y2 , а це є суперечність, яка виникла внаслідок

припущення, що f

(x)

є не зростаючою функцією. ■

Наслідок. Нехай

функція

y = f (x)

визначена, неперервна і є

зростаючою (спадною) на скінченному або нескінченному

проміжку

a;b .

Тоді обернена

функція

x = f −1 (y) існує

(визначена), неперервна і є зростаючою (спадною) на проміжку

A; B , де

A = lim f

(x); B = lim f

(x)

– у випадку зростання функції f (x),

x→a+0

x→b−0

A = lim f

(x);

B = lim f

(x) – у випадку спадання функції f (x).

x→b−0

x→a+0

Наслідок доведіть самостійно.

Розглянемо обернені функції для деяких елементарних функцій, відомих вам ще з шкільного курсу математики.

193

Обернені тригонометричні функції, їх неперервність.

	y = sinx	y = arcsinx
	Y
	y=sinx	π/2
	1
	−π/2	X
	0
		π/2
	-1
		π/2

1. D(sin) =

π

;

π

1.

D(arcsin) =[−1;1],

−

2

,

π

π

2

;

E(sin) =[−1;1].

E(arcsin) = −

2

.

2

2.

неперервна,

2.

неперервна,

3.

зростає,

3.

зростає,

4.

контрольні точки графіка:

4.

контрольні точки графіка:

π

(0;0),

π

−1;−

π

(0;0),

π

−

2

;−1 ,

;1

2

,

1;

2

2

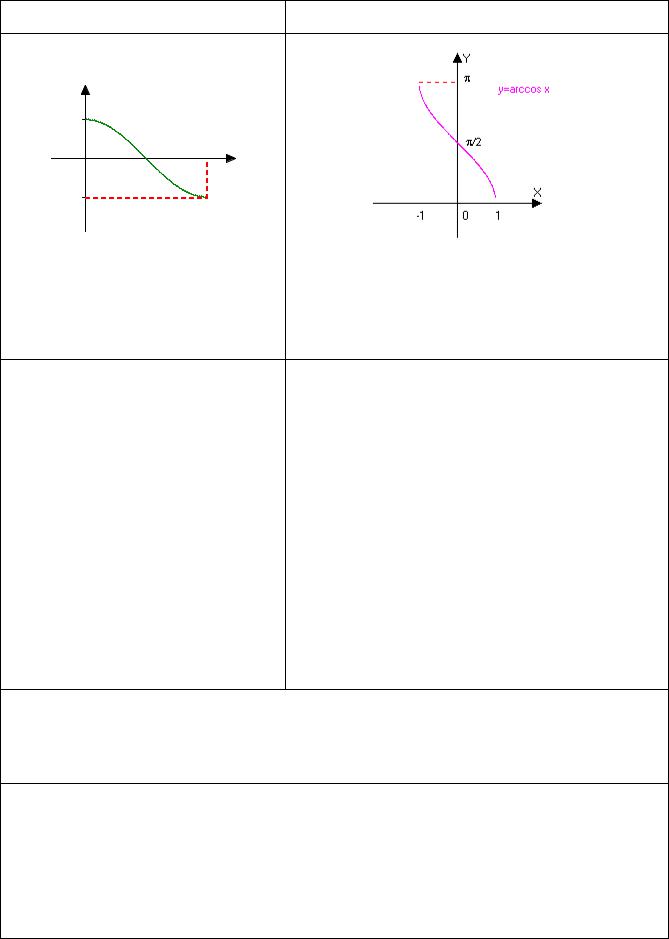
За теоремою 16.2 існує функція, обернена до y = sin x , яку позначимо y = arcsin x .

Означення 16.2. Арксинусом числа а називається величина кута з

відрізка	−	π	;	π		, синус якого дорівнює а:
		2		2
						sin (arcsin a)= a,
						arcsin (−a)= −arcsin a.

194

y = cosx

y = arccosx

Y
1	y=cosx
π/2	π X
0
-1

1.	D(cos) =[0;π ],					1.	D(arccos) =[−1;1], E(arccos) =[0;π].
E(cos) =[−1;1].						2.	неперервна,
2.	неперервна,					3.	спадає,
3.	спадає,					4.	контрольні точки графіка:
4.	контрольні точки графіка:						(1;0),	0; π	, (−1;π ).
		π	;0		(π;−1).			2
	(0;1),	2		,

За теоремою 16.2 існує функція, обернена до y = cos x , яку позначаємо y = arccos x

Означення 16.3. Арккосинусом числа а називається величина кута з відрізка [0;π], косинус якого дорівнює а:

cos (arccos a)= a,

arccos(−a)= π − arccos a.

195

y = tgx

y = arctgx

	Y
	y=tgx
	1	X
−π/2	0	π/4 π/2
	-1

1. D(tg) =

−π ;

π

,

1.

D(arctg) = (−∞;∞),

2

2

−

π

;

π

E(tg) = (−∞;+∞).

E(arctg) =

2

2

,

2. неперервна,

2.

неперервна,

3.

зростає,

3. зростає,

π

π

4. (0;0), lim tgx = +∞;

4.

(0;0), lim arctgx =

;

lim tgx =

.

π

2

2

x→

2 −0

x→+∞

x→−∞

lim tgx = −∞.

x→π +0

2

За наслідком з теореми 16.2 існує функція, обернена до

y = tgx, яку

позначаємо

y = arctgx .

Означення 16.4. Арктангенсом числа а називається величина кута

з інтервалу	−	π	;	π		, тангенс якого дорівнює а:
		2		2
						tg (arctga)= a,
						arctg (−a)= −arctga..

196

Л огарифмічна функція.

			Y
3	Y		a>1
	a>1
2			X
1	0<a<1X	0	1
0			0<a<1

				(log) = (
1 . D(ax ) = (−∞;+∞),		1. D				0;+∞), E(log) = (−∞;+∞).
E(ax ) = (0;+∞).		2. неперервна,
2 . неперервна.		3. При a>1 зростає:
3 . При a >1 зростає:
	,		При 0<a<1 спадає:
При 0<a<1 спадає:
										.
	.
		4.			Графік		проходить			через
4 . Графік проходить через
		точку (1;0)
точку (0;1)			Якщо a>1, то
Якщо a>1, то
			li m loga x = +∞,					lim loga x = −∞.
lim ax = +∞, lim ax = 0 .
			x→+∞					x→0+0
x→+∞	x→−∞		Якщо 0<a<1, то
Якщо 0<a<1, то
			li m loga x = +∞,					lim loga x	= −∞.
lim ax = 0,	lim ax = +∞.
			x→0+0					x→+∞
x→+∞	x→−∞
За наслідком з теореми 16.2 існ					ує функція, обернена до					y = ax ,
яку позначаємо y = loga x .

Означення 16.5. Логарифмом числа при основі а називається показник степеня, до якого потрібно піднести основу а, щоб отримати число x :

.

197

Властивості логарифма:

1.

loga

x1 x2 = loga

x1 +loga

x2 ,

x1 > 0, x2 > 0 .

2.

loga

x p

= p loga

x, x > 0, p R .

3.

log

a

x1

= log

a

x

−log

a

x

,

x > 0, x

> 0 .

x

1

2

1

2

2

Степене ва функція.

Означення 16.6. Функція

y = xα ,

α R називається степенево ю

функцією з дійсним показником .

Теорема 1 6.3. Степенева функція y = xα неперервна x > 0.

До ведення.

З означення логарифма маємо: x = eln x

xα = eα ln x .

Тому y = xα є компози ція показникової функції y = eu і логарифмічної

функції u =α ln x . А оскільки ці функції неперервні і

E (α ln x)= R = D(e u ),

то і композиція їх є неперервна функція. ■

198

План:

1.Означення диференційовної функції, її неперервність. Похідна і диференціал.

2.Односторонні похідні.

3.Нескінченні похідні.

Означення диференційовної функції, її неперервність. Похідна і диференціал.

Означення 17.1. Нехай функція			y = f (x) визначена в деякому
околі точки x0 і нехай		x O(x0 ).	Якщо існує скінченна границя
відношення приросту функції f (x) до приросту аргумента:
lim	f	(x)− f (x0 )		,
		x − x0
x→x0

то вона називається похідною функції y = f (x) в точці x0 , а сама функція називається диференційовною в цій точці.

Позначення похідної:							(17.1)
Як відомо приріст незалежної змінної позначають							x = x − x0 , а
приріст функції f (x) в точці x0 : f (x0 )= f (x)− f (x0 ). Тоді формулу
(17.1) запишемо у вигляді:
						,	(17.2)
або							(17.3)

199